【班海精品】青岛版(2015)六下-第二单元 2.圆柱与圆锥的体积【优质课件】
文档属性
| 名称 | 【班海精品】青岛版(2015)六下-第二单元 2.圆柱与圆锥的体积【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
圆柱与圆柱的
体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目
录
课前导入
新课精讲
学以致用
课堂小结
1
01
02
03
04
课前导入
情景导入
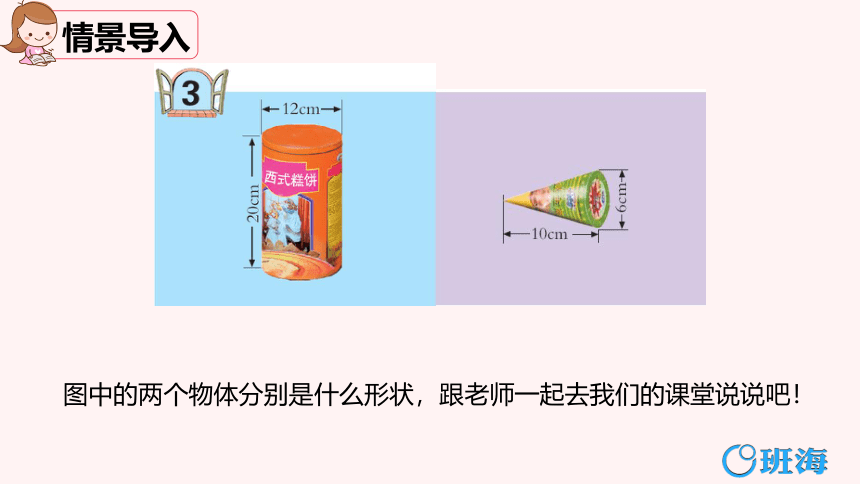
图中的两个物体分别是什么形状,跟老师一起去我们的课堂说说吧!
新课精讲
探索新知
根据这些信息,你能提出什么问题?
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm,高是20cm。
圆柱形包装盒的体积是多少立方厘米?
探索新知
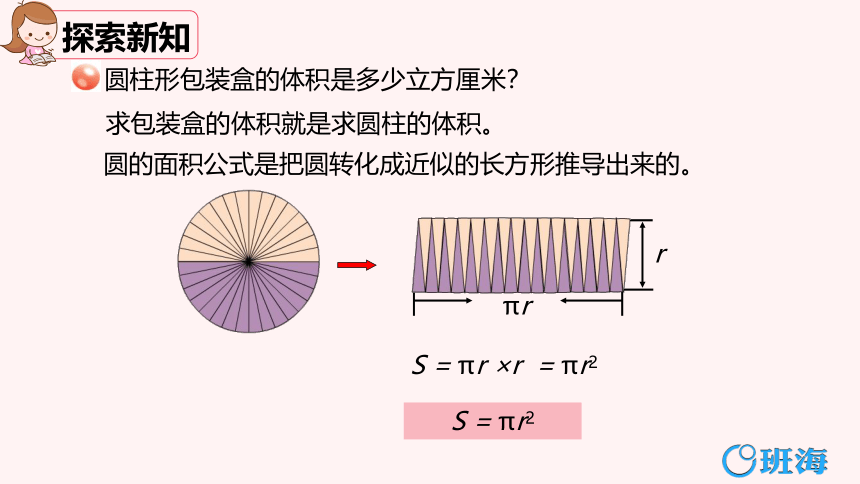
πr
S = πr ×r = πr2
S = πr2
r
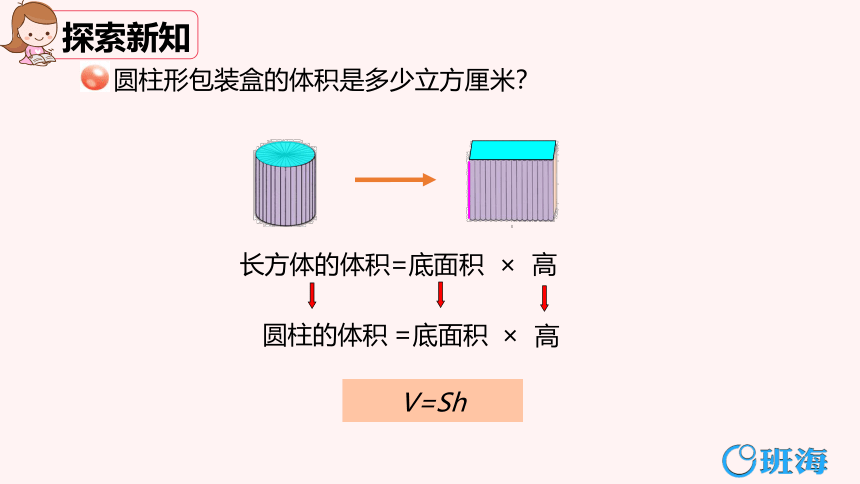
圆柱形包装盒的体积是多少立方厘米?
求包装盒的体积就是求圆柱的体积。
圆的面积公式是把圆转化成近似的长方形推导出来的。
探索新知
?
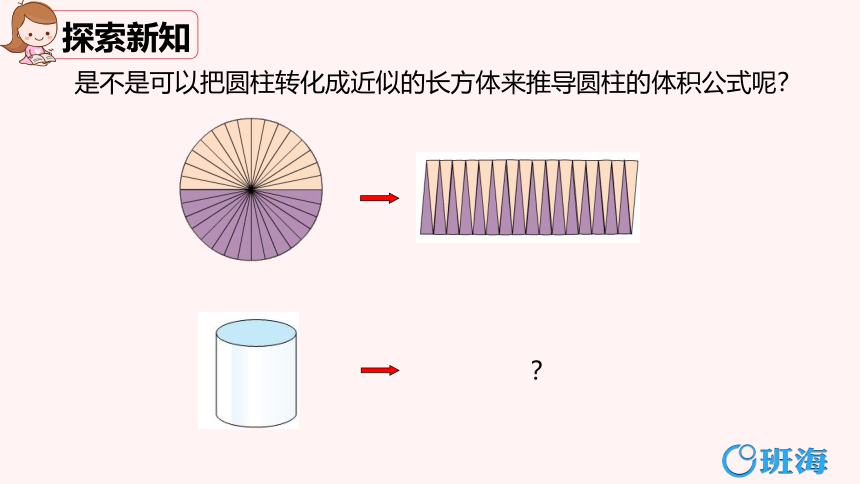
是不是可以把圆柱转化成近似的长方体来推导圆柱的体积公式呢?
探索新知
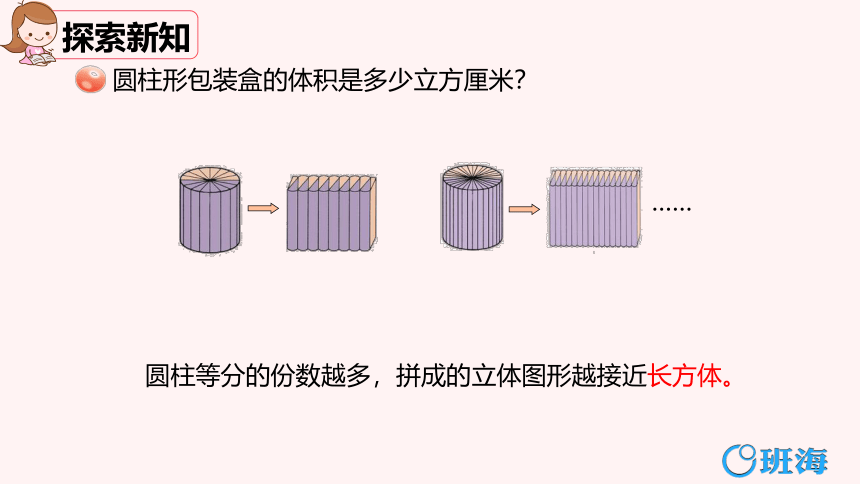
圆柱形包装盒的体积是多少立方厘米?
圆柱等分的份数越多,拼成的立体图形越接近长方体。
……
探索新知
V=Sh
圆柱形包装盒的体积是多少立方厘米?
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
探索新知
底面积: 3.14×(12÷2)2
= 3.14×36
= 113.04(cm2)
体积:113.04×20 = 2260.8(cm3)
答:这个圆柱形包装盒的体积是2260.8 cm3 。
圆柱形包装盒的体积是多少立方厘米?
探索新知
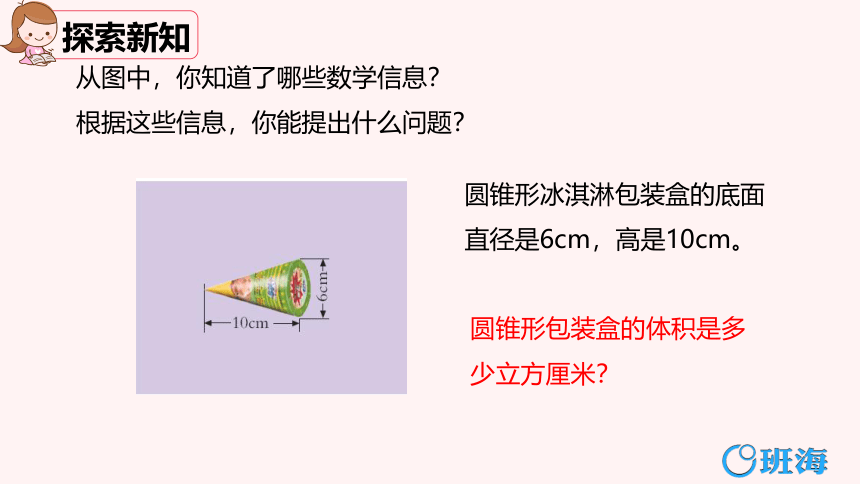
从图中,你知道了哪些数学信息?
圆锥形冰淇淋包装盒的底面直径是6cm,高是10cm。
圆锥形包装盒的体积是多少立方厘米?
根据这些信息,你能提出什么问题?
探索新知
求圆锥形包装盒的体积就是求圆锥的体积。
猜一猜:圆锥的体积可能与哪种立体图形的体积有关系?
圆锥形包装盒的体积是多少立方厘米?
怎样求圆锥的体积呢?
探索新知
这个圆柱和圆锥等底等高。
圆锥的体积与圆柱有怎样的关系呢?
●
●
探索新知
实验活动要求
(1)材料:等底等高的圆柱形、圆锥形容器各一个;适量的沙子。
(2)方法一:将圆锥形容器装满沙子,再倒入圆柱形的容器里,倒满为止。
方法二:将圆柱形容器装满沙子,再倒入圆锥形的容器里,倒完为止。
(3)你有什么发现?由此可以得出什么结论?
圆锥的体积与圆柱有怎样的关系呢?
我们来做个实验看看。
探索新知
我们来做个实验看看。
圆锥的体积与圆柱有怎样的关系呢?
探索新知
Ⅴ= Sh
1
3
圆锥的体积与圆柱有怎样的关系呢?
·
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积= × 底面积×高
探索新知
= 94.2(cm3)
= ×3.14×9×10
1
3
× 3.14×(6÷2)2 ×10
1
3
圆锥形包装盒的体积是多少立方厘米?
答:这个圆锥形包装盒的体积是94.2 cm3 。
典题精讲
一、我会填。
1.把圆柱的底面分成许多相等的扇形,再按照这些扇形沿着圆柱的高把圆柱切开,拼起来,得到一个近似的( ),它的底面积等于圆柱的( ),它的高等于圆柱的( ),它的体积和圆柱的体积( )。
2.圆柱的体积=( ),用字母表示为V=( )。
长方体
底面积
相等
高
底面积×高
Sh
典题精讲
二、算一算,填一填。
1.如下图,一根圆木的横截面面积是2.5 dm2,高是10 dm,它的体积是( )dm3。
2.一个圆柱的体积是80 cm3,底面积是16 cm2,高是( )cm。
5
25
典题精讲
三、求下面圆柱的体积。
3.14×52×12=942(dm3)
2.
3.14×(4÷2)2×12=150.72(cm3)
1.
典题精讲
四、妈妈的茶杯形状如下图,一天我给妈妈泡了满满一杯茶。这杯茶有多少毫升?(茶杯厚度忽略不计)
3.14×(6÷2)2×14=395.64(cm3)
395.64 cm3=395.64 mL
答:这杯茶有395.64 mL。
典题精讲
五、认真填一填。
1.一个圆锥形容器内装满水,倒入与它等底等高的圆柱形容器内,需倒( )次才能倒满。
2.一个圆柱和一个圆锥的高相等,底面积也相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的( )。
3
3倍
典题精讲
3.3个圆柱形铅锭可以熔铸成( )个与它等底等高的圆锥。
4.一个圆锥的底面积是15平方分米,高是6分米,它的体积是( ),与它等底等高的圆柱的体积是( )。
5.一个高为15厘米的圆锥形容器中装满了水,将水倒入一个与它等底等高的圆柱形容器中,水面高( )厘米。
9
30立方分米
5
90立方分米
典题精讲
二、计算下面圆锥的体积。(单位:厘米)
1.
×3.14×(18÷2)2×7.5=635.85(立方厘米)
2.
18.84÷3.14÷2=3(厘米)
×3.14×32×24=226.08(立方厘米)
易错提醒
小法官,巧判断。
1.圆柱的体积一定比它的表面积大。 ( )
辨析:透彻理解圆柱体积。“1”中两个概念所表示的意义不同,无法比较。
×
2.侧面积相等的两个圆柱,它们的体积一定相等。 ( )
3.圆柱的底面半径越大,它的体积就越大。 ( )
辨析:透彻理解圆柱体积。 “2”中圆柱的侧面积和体积都与圆柱的底面半径与高相关,侧面积相等的两个圆柱,体积未必相等。
×
×
易错提醒
4.如果一个圆锥的体积等于一个圆柱体积的 ,那么它们一定等底等高。 ( )
5.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的2倍。 ( )
辨析:正确判断圆柱和圆锥体积之间的关系。“5”中将圆锥体积看成1份,圆柱体积是3份,削去部分的体积为2份。
×
√
易错提醒
6.圆锥的体积是圆柱体积的 。 ( )
7.体积相等的圆锥和圆柱,如果它们的高也相等,那么圆锥的底面积就是圆柱底面积的3倍。 ( )
×
√
辨析:正确判断圆柱和圆锥体积之间的关系。圆锥的体积是与它等底等高的圆柱体积的 。
学以致用
小试牛刀
1.求下列图形的体积。(单位:厘米)
3.14×(8÷2)2×8
= 401.92(cm )
3.14×(4÷2)2×10
= 125.6(cm )
小试牛刀
= 3.14×2.25×2
×3.14×(3÷2)2×6
1
3
×3.14×22×4.5
1
3
= 14.13(dm3)
= 3.14×4×1.5
= 18.84(dm3)
小试牛刀
2.求下列圆锥的体积。
×5.6×3
1
3
(1)S=5.6dm2 h=3dm
(2)r=6cm h=20cm
(3)d=8m h=6m
= 5.6(dm3)
×3.14×62×20
1
3
= ×3.14×36×20
1
3
= 753.6(cm3)
×3.14×(8÷2)2×6
1
3
= ×3.14×16×6
1
3
= 100.48(m3)
小试牛刀
3.哪一根木料的体积大?
3.14×(0.6÷2)2×8
= 3.14×0.09×8
= 2.2608(m3)
3.14×(0.4÷2)2×10
= 3.14×0.04×10
= 1.256(m3)
1.256<2.2608
答:第二根木料的体积大。
小试牛刀
4.
有一个圆柱形油桶,从里面量底面直径是40厘米,高是50厘米。(1)它的容积是多少升?
(2)若1升柴油重0.85千克,则这个油桶可装多少千克柴油?
3.14×(40÷2)2×50
= 3.14×400×50
= 62800(cm3)
= 62.8 (L)
答:它的容积是62.8升。
0.85×62.8=53.38(千克)
答:这个油桶可装53.38千克柴油。
小试牛刀
= 3.14×25×0.8
= 62.8(m3)
62.8×1.4 = 87.92(吨)
答:这堆煤大约重87.92吨。
×3.14×(31.4÷3.14÷2)2×2.4
1
3
5. 一个近似圆锥形的煤堆,测得它的底面周长是31.4米,高是2.4米,如果每立方米煤重1.4吨,这堆煤大约重多少吨?
课堂小结
1.利用转化思想把圆柱转化成长方体,从而推导出圆柱的体积=底面积×高,用字母表示为V=Sh。
2.圆锥的体积等于和它等底等高的圆柱体积的三分之一。圆锥的体积=底面积×高× ,字母公式为V= Sh。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
圆柱与圆柱的
体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目
录
课前导入
新课精讲
学以致用
课堂小结
1
01
02
03
04
课前导入
情景导入
图中的两个物体分别是什么形状,跟老师一起去我们的课堂说说吧!
新课精讲
探索新知
根据这些信息,你能提出什么问题?
从图中,你知道了哪些数学信息?
圆柱形包装盒的底面直径是12cm,高是20cm。
圆柱形包装盒的体积是多少立方厘米?
探索新知
πr
S = πr ×r = πr2
S = πr2
r
圆柱形包装盒的体积是多少立方厘米?
求包装盒的体积就是求圆柱的体积。
圆的面积公式是把圆转化成近似的长方形推导出来的。
探索新知
?
是不是可以把圆柱转化成近似的长方体来推导圆柱的体积公式呢?
探索新知
圆柱形包装盒的体积是多少立方厘米?
圆柱等分的份数越多,拼成的立体图形越接近长方体。
……
探索新知
V=Sh
圆柱形包装盒的体积是多少立方厘米?
底面积
高
圆柱的体积
=
×
长方体的体积=底面积 × 高
探索新知
底面积: 3.14×(12÷2)2
= 3.14×36
= 113.04(cm2)
体积:113.04×20 = 2260.8(cm3)
答:这个圆柱形包装盒的体积是2260.8 cm3 。
圆柱形包装盒的体积是多少立方厘米?
探索新知
从图中,你知道了哪些数学信息?
圆锥形冰淇淋包装盒的底面直径是6cm,高是10cm。
圆锥形包装盒的体积是多少立方厘米?
根据这些信息,你能提出什么问题?
探索新知
求圆锥形包装盒的体积就是求圆锥的体积。
猜一猜:圆锥的体积可能与哪种立体图形的体积有关系?
圆锥形包装盒的体积是多少立方厘米?
怎样求圆锥的体积呢?
探索新知
这个圆柱和圆锥等底等高。
圆锥的体积与圆柱有怎样的关系呢?
●
●
探索新知
实验活动要求
(1)材料:等底等高的圆柱形、圆锥形容器各一个;适量的沙子。
(2)方法一:将圆锥形容器装满沙子,再倒入圆柱形的容器里,倒满为止。
方法二:将圆柱形容器装满沙子,再倒入圆锥形的容器里,倒完为止。
(3)你有什么发现?由此可以得出什么结论?
圆锥的体积与圆柱有怎样的关系呢?
我们来做个实验看看。
探索新知
我们来做个实验看看。
圆锥的体积与圆柱有怎样的关系呢?
探索新知
Ⅴ= Sh
1
3
圆锥的体积与圆柱有怎样的关系呢?
·
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积= × 底面积×高
探索新知
= 94.2(cm3)
= ×3.14×9×10
1
3
× 3.14×(6÷2)2 ×10
1
3
圆锥形包装盒的体积是多少立方厘米?
答:这个圆锥形包装盒的体积是94.2 cm3 。
典题精讲
一、我会填。
1.把圆柱的底面分成许多相等的扇形,再按照这些扇形沿着圆柱的高把圆柱切开,拼起来,得到一个近似的( ),它的底面积等于圆柱的( ),它的高等于圆柱的( ),它的体积和圆柱的体积( )。
2.圆柱的体积=( ),用字母表示为V=( )。
长方体
底面积
相等
高
底面积×高
Sh
典题精讲
二、算一算,填一填。
1.如下图,一根圆木的横截面面积是2.5 dm2,高是10 dm,它的体积是( )dm3。
2.一个圆柱的体积是80 cm3,底面积是16 cm2,高是( )cm。
5
25
典题精讲
三、求下面圆柱的体积。
3.14×52×12=942(dm3)
2.
3.14×(4÷2)2×12=150.72(cm3)
1.
典题精讲
四、妈妈的茶杯形状如下图,一天我给妈妈泡了满满一杯茶。这杯茶有多少毫升?(茶杯厚度忽略不计)
3.14×(6÷2)2×14=395.64(cm3)
395.64 cm3=395.64 mL
答:这杯茶有395.64 mL。
典题精讲
五、认真填一填。
1.一个圆锥形容器内装满水,倒入与它等底等高的圆柱形容器内,需倒( )次才能倒满。
2.一个圆柱和一个圆锥的高相等,底面积也相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的( )。
3
3倍
典题精讲
3.3个圆柱形铅锭可以熔铸成( )个与它等底等高的圆锥。
4.一个圆锥的底面积是15平方分米,高是6分米,它的体积是( ),与它等底等高的圆柱的体积是( )。
5.一个高为15厘米的圆锥形容器中装满了水,将水倒入一个与它等底等高的圆柱形容器中,水面高( )厘米。
9
30立方分米
5
90立方分米
典题精讲
二、计算下面圆锥的体积。(单位:厘米)
1.
×3.14×(18÷2)2×7.5=635.85(立方厘米)
2.
18.84÷3.14÷2=3(厘米)
×3.14×32×24=226.08(立方厘米)
易错提醒
小法官,巧判断。
1.圆柱的体积一定比它的表面积大。 ( )
辨析:透彻理解圆柱体积。“1”中两个概念所表示的意义不同,无法比较。
×
2.侧面积相等的两个圆柱,它们的体积一定相等。 ( )
3.圆柱的底面半径越大,它的体积就越大。 ( )
辨析:透彻理解圆柱体积。 “2”中圆柱的侧面积和体积都与圆柱的底面半径与高相关,侧面积相等的两个圆柱,体积未必相等。
×
×
易错提醒
4.如果一个圆锥的体积等于一个圆柱体积的 ,那么它们一定等底等高。 ( )
5.把一个圆柱削成一个最大的圆锥,削去部分的体积是圆锥体积的2倍。 ( )
辨析:正确判断圆柱和圆锥体积之间的关系。“5”中将圆锥体积看成1份,圆柱体积是3份,削去部分的体积为2份。
×
√
易错提醒
6.圆锥的体积是圆柱体积的 。 ( )
7.体积相等的圆锥和圆柱,如果它们的高也相等,那么圆锥的底面积就是圆柱底面积的3倍。 ( )
×
√
辨析:正确判断圆柱和圆锥体积之间的关系。圆锥的体积是与它等底等高的圆柱体积的 。
学以致用
小试牛刀
1.求下列图形的体积。(单位:厘米)
3.14×(8÷2)2×8
= 401.92(cm )
3.14×(4÷2)2×10
= 125.6(cm )
小试牛刀
= 3.14×2.25×2
×3.14×(3÷2)2×6
1
3
×3.14×22×4.5
1
3
= 14.13(dm3)
= 3.14×4×1.5
= 18.84(dm3)
小试牛刀
2.求下列圆锥的体积。
×5.6×3
1
3
(1)S=5.6dm2 h=3dm
(2)r=6cm h=20cm
(3)d=8m h=6m
= 5.6(dm3)
×3.14×62×20
1
3
= ×3.14×36×20
1
3
= 753.6(cm3)
×3.14×(8÷2)2×6
1
3
= ×3.14×16×6
1
3
= 100.48(m3)
小试牛刀
3.哪一根木料的体积大?
3.14×(0.6÷2)2×8
= 3.14×0.09×8
= 2.2608(m3)
3.14×(0.4÷2)2×10
= 3.14×0.04×10
= 1.256(m3)
1.256<2.2608
答:第二根木料的体积大。
小试牛刀
4.
有一个圆柱形油桶,从里面量底面直径是40厘米,高是50厘米。(1)它的容积是多少升?
(2)若1升柴油重0.85千克,则这个油桶可装多少千克柴油?
3.14×(40÷2)2×50
= 3.14×400×50
= 62800(cm3)
= 62.8 (L)
答:它的容积是62.8升。
0.85×62.8=53.38(千克)
答:这个油桶可装53.38千克柴油。
小试牛刀
= 3.14×25×0.8
= 62.8(m3)
62.8×1.4 = 87.92(吨)
答:这堆煤大约重87.92吨。
×3.14×(31.4÷3.14÷2)2×2.4
1
3
5. 一个近似圆锥形的煤堆,测得它的底面周长是31.4米,高是2.4米,如果每立方米煤重1.4吨,这堆煤大约重多少吨?
课堂小结
1.利用转化思想把圆柱转化成长方体,从而推导出圆柱的体积=底面积×高,用字母表示为V=Sh。
2.圆锥的体积等于和它等底等高的圆柱体积的三分之一。圆锥的体积=底面积×高× ,字母公式为V= Sh。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
