【班海精品】青岛版(2015)六下-第三单元 6.用比例解决实际问题【优质课件】
文档属性
| 名称 | 【班海精品】青岛版(2015)六下-第三单元 6.用比例解决实际问题【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
用
用比例解决实际问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1
课前导入
3
学以致用
2
新课精讲
4
课堂小结
目 录
课前导入
1
情景导入
图中的工人师傅们在往货车上装啤酒,让我们一起看看师傅们装的怎么样吧!
新课精讲
2
探索新知
根据这些信息,你能提出什么问题?
从图中,你了解到哪些数学信息?
2个箱子能装24瓶啤酒。
现有480瓶啤酒。
需要几个箱子?
一批啤酒用载重8吨的汽车运,
需要15辆。现在改用载重10
吨的汽车运……
2个箱子能装24瓶啤酒。
现有480瓶啤酒……
一批啤酒用载重8吨的
汽车运,需要15辆;现改用载重10吨的汽车运。
需要几辆汽车?
探索新知
想一想,啤酒的总瓶数和所需要的箱数成什么关系?
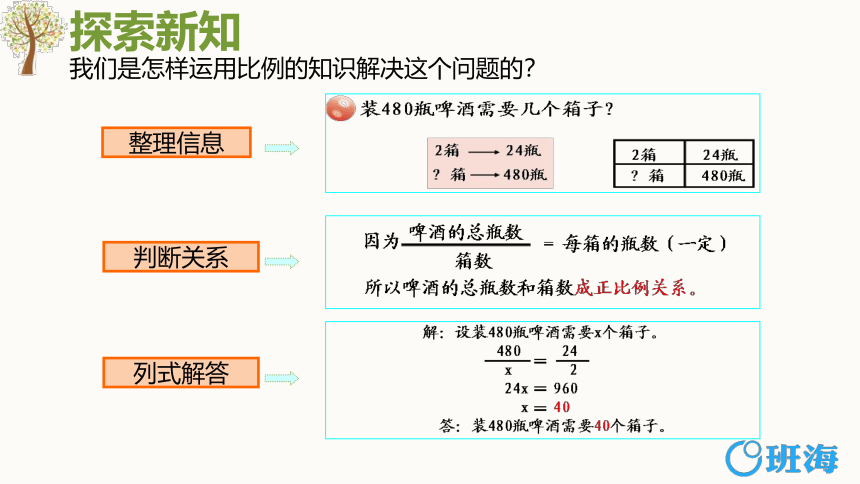
解:设装480瓶啤酒需要x 个箱子。
480 24
x 2
24x 960
x 40
答:装480瓶啤酒需要40个箱子。
=
=
=
装480瓶啤酒需要几个箱子?
所以啤酒的总瓶数和箱数成正比例。
2箱 24瓶
?箱 480瓶
2箱 24瓶
?箱 480瓶
= 每箱的瓶数(一定)
啤酒的总瓶数
箱数
因为
先整理一下条件和问题,再解答。
探索新知
我们是怎样运用比例的知识解决这个问题的?
整理信息
判断关系
列式解答
探索新知
8吨 15辆
10箱 ?辆
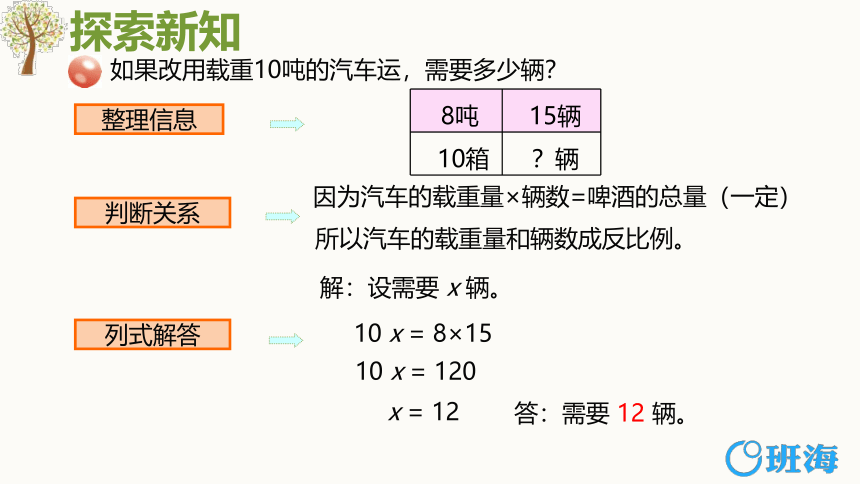
因为汽车的载重量×辆数=啤酒的总量(一定)
解:设需要 x 辆。
如果改用载重10吨的汽车运,需要多少辆?
整理信息
判断关系
列式解答
所以汽车的载重量和辆数成反比例。
x = 12
10 x = 8×15
10 x = 120
答:需要 12 辆。
探索新知
想一想,解正反比例问题的步骤是怎样的?
运用比例知识解决实际问题的关键是什么?
整理信息
判断关系
列式解答
判断关系
典题精讲
一、轻松填空。
1.汽车2小时行驶120千米,照这样计算,4小时能行驶多少千米?
(1)“照这样计算”就是说( )是一定的。
(2)路程和时间成( )比例。
(3)列出关系式是 =( )(一定)。
(4)设4小时能行驶x千米,写出比例式是( )。
速度
正
路程时间
( )
( )
速度
=
2.明明5分钟打75个字,照这样计算,打一篇1800字的文章需x分钟。
根据___________________=________________(一定),写出比例式:_____________________。
打字总数 ∶时间
每分钟打字数
75 ∶5=1800 ∶x
典题精讲
二、妈妈买了一瓶蜂蜜,从商标纸上可以知道,100克蜂蜜里含有34.5克葡萄糖。照这样计算,3000克蜂蜜里含有多少克葡萄糖?(先列比例解,再用算术法解)
(列比例) 解:设3000克蜂蜜里含有x 克葡萄糖。
=
x=1035
(算术法) 34.5÷100×3000=1035(克)
答:3000克蜂蜜里含有1035克葡萄糖。
典题精讲
三、填一填。
1.有一堆煤,计划每天烧105 kg,可以烧30天。改进炉灶后,每天只烧90 kg,这堆煤实际可以烧多少天?
“有一堆煤”,就是说( )一定。
( )和( )成反比例。
煤的总数
烧的天数
每天烧煤数
(3) 关系式是( )×( )=( )(一定)。
(4) 设这堆煤实际可以烧x天,写出比例式是( )。
烧的天数
每天烧煤数
煤的总数
90x=105×30
典题精讲
2.一批水果,若每箱装12千克,正好可以装30箱,如果每箱装x 千克,可以装24箱。
根据_______________________________=______________(一定),
写出比例式:_____________________。
每箱装水果的千克数×箱数
24x=12×30
水果总数
典题精讲
四、某建筑公司要运一批沙子,若每天运24车,需要4天运完。现在需要3天运完,每天应运多少车?(列比例解)
解:设每天应运 x 车。
3x=24×4
x=32
答:每天应运32车。
易错提醒
判断对错。
1.一对相互咬合的齿轮,主动轮有80个齿,每分钟转100转,从动轮有25个齿,每分钟转多少转?设从动轮每分钟转 x 转,列比例式为 = 。 ( )
辨析:对比例的基本性质理解不透彻。齿轮齿数和每分钟转数成反比例,所以列比例式应为25x=80×100。
×
×
2.80千克花生可榨油32千克,榨150吨花生油要用多少吨花生?设要用x吨花生,列比例式为 = 。 ( )
辨析:对比例的基本性质理解不透彻。花生数量和出油量成正比例。
学以致用
3
小试牛刀
1.
解:设5小时游 x 千米。
x = 350
答:5小时游 350 千米。
x
140
5
=
2
“海上霸王”大白鲨2小时游140千米,照这样的速度,5小时游多少千米?
= 速度(一定),所以路程和时间成正比例。
因为
路程
时间
小试牛刀
2.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?
解:设如果每行站16人,能站 x 行。
每行的人数×行数=总人数(一定),每行的人数和行数成反比例。
16 x = 20×12
16 x = 240
x = 15
答:如果每行站16人,能站15行。
小试牛刀
3.
学校计划用方砖铺微机室地面,如果用边长5分米的方砖,需要用360块;如果改用边长6分米的方砖,需要多少块?
解:设如果改用边长6分米的,需要 x 块。
每块方砖的面积×块数=地面面积(一定)
6×6× x = 5×5×360
36 x = 9000
x = 250
答:如果改用边长6分米的,需要250块。
小试牛刀
4.
(1)明新骑车从甲地到乙地,前5分钟行了700米,照这样的速度,从甲地到乙地一共用了20分钟。甲、乙两地相距多少米?
路程
时间
= 速度(一定)
700
5
x
20
20
=
5 x = 14000
x = 2800
答:甲乙两地相距2800米。
解:甲乙两地相距 x 米。
小试牛刀
4.
解:返回时用了x 分钟。
(2)明新骑车从甲地到乙地一共用了20分钟,每分钟行140米;返回时每分钟行100米,返回时用了多少分钟?
速度×时间 = 路程(一定)
100× x = 140×20
100 x = 2800
答:返回时用了28分钟。
x = 28
小试牛刀
5.
解:设他的车模的速度是每分钟 x 米。
速度×时间 = 路程(一定)
学校举行四驱车模比赛。小强的车模速度为480米/分,跑完全程用了5分钟。小瑞的车模跑完全程比小强的多用了1分钟,他的车模速度是多少?
6 x = 2400
(5+1)x = 480×5
答:他的车模的速度是每分钟400米。
x = 400
课堂小结
4
用正比例知识解决问题的步骤:
(1)找量。找到两种相关联的量及不变的量;
(2)判断。判断两种相关联的量是否成正比例;
(3)列式求解。设未知数,列比例式并求解;
(4)检验并写出答语。
用反比例知识解决问题的步骤:
(1)找量。找到两种相关联的量及不变的量;
(2)判断。判断两种相关联的量是否成反比例;
(3)列式求解。设未知数,列方程并求解;
(4)检验并写出答语。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
用
用比例解决实际问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1
课前导入
3
学以致用
2
新课精讲
4
课堂小结
目 录
课前导入
1
情景导入
图中的工人师傅们在往货车上装啤酒,让我们一起看看师傅们装的怎么样吧!
新课精讲
2
探索新知
根据这些信息,你能提出什么问题?
从图中,你了解到哪些数学信息?
2个箱子能装24瓶啤酒。
现有480瓶啤酒。
需要几个箱子?
一批啤酒用载重8吨的汽车运,
需要15辆。现在改用载重10
吨的汽车运……
2个箱子能装24瓶啤酒。
现有480瓶啤酒……
一批啤酒用载重8吨的
汽车运,需要15辆;现改用载重10吨的汽车运。
需要几辆汽车?
探索新知
想一想,啤酒的总瓶数和所需要的箱数成什么关系?
解:设装480瓶啤酒需要x 个箱子。
480 24
x 2
24x 960
x 40
答:装480瓶啤酒需要40个箱子。
=
=
=
装480瓶啤酒需要几个箱子?
所以啤酒的总瓶数和箱数成正比例。
2箱 24瓶
?箱 480瓶
2箱 24瓶
?箱 480瓶
= 每箱的瓶数(一定)
啤酒的总瓶数
箱数
因为
先整理一下条件和问题,再解答。
探索新知
我们是怎样运用比例的知识解决这个问题的?
整理信息
判断关系
列式解答
探索新知
8吨 15辆
10箱 ?辆
因为汽车的载重量×辆数=啤酒的总量(一定)
解:设需要 x 辆。
如果改用载重10吨的汽车运,需要多少辆?
整理信息
判断关系
列式解答
所以汽车的载重量和辆数成反比例。
x = 12
10 x = 8×15
10 x = 120
答:需要 12 辆。
探索新知
想一想,解正反比例问题的步骤是怎样的?
运用比例知识解决实际问题的关键是什么?
整理信息
判断关系
列式解答
判断关系
典题精讲
一、轻松填空。
1.汽车2小时行驶120千米,照这样计算,4小时能行驶多少千米?
(1)“照这样计算”就是说( )是一定的。
(2)路程和时间成( )比例。
(3)列出关系式是 =( )(一定)。
(4)设4小时能行驶x千米,写出比例式是( )。
速度
正
路程时间
( )
( )
速度
=
2.明明5分钟打75个字,照这样计算,打一篇1800字的文章需x分钟。
根据___________________=________________(一定),写出比例式:_____________________。
打字总数 ∶时间
每分钟打字数
75 ∶5=1800 ∶x
典题精讲
二、妈妈买了一瓶蜂蜜,从商标纸上可以知道,100克蜂蜜里含有34.5克葡萄糖。照这样计算,3000克蜂蜜里含有多少克葡萄糖?(先列比例解,再用算术法解)
(列比例) 解:设3000克蜂蜜里含有x 克葡萄糖。
=
x=1035
(算术法) 34.5÷100×3000=1035(克)
答:3000克蜂蜜里含有1035克葡萄糖。
典题精讲
三、填一填。
1.有一堆煤,计划每天烧105 kg,可以烧30天。改进炉灶后,每天只烧90 kg,这堆煤实际可以烧多少天?
“有一堆煤”,就是说( )一定。
( )和( )成反比例。
煤的总数
烧的天数
每天烧煤数
(3) 关系式是( )×( )=( )(一定)。
(4) 设这堆煤实际可以烧x天,写出比例式是( )。
烧的天数
每天烧煤数
煤的总数
90x=105×30
典题精讲
2.一批水果,若每箱装12千克,正好可以装30箱,如果每箱装x 千克,可以装24箱。
根据_______________________________=______________(一定),
写出比例式:_____________________。
每箱装水果的千克数×箱数
24x=12×30
水果总数
典题精讲
四、某建筑公司要运一批沙子,若每天运24车,需要4天运完。现在需要3天运完,每天应运多少车?(列比例解)
解:设每天应运 x 车。
3x=24×4
x=32
答:每天应运32车。
易错提醒
判断对错。
1.一对相互咬合的齿轮,主动轮有80个齿,每分钟转100转,从动轮有25个齿,每分钟转多少转?设从动轮每分钟转 x 转,列比例式为 = 。 ( )
辨析:对比例的基本性质理解不透彻。齿轮齿数和每分钟转数成反比例,所以列比例式应为25x=80×100。
×
×
2.80千克花生可榨油32千克,榨150吨花生油要用多少吨花生?设要用x吨花生,列比例式为 = 。 ( )
辨析:对比例的基本性质理解不透彻。花生数量和出油量成正比例。
学以致用
3
小试牛刀
1.
解:设5小时游 x 千米。
x = 350
答:5小时游 350 千米。
x
140
5
=
2
“海上霸王”大白鲨2小时游140千米,照这样的速度,5小时游多少千米?
= 速度(一定),所以路程和时间成正比例。
因为
路程
时间
小试牛刀
2.六年级同学做广播操,每行站20人,正好站12行。如果每行站16人,能站多少行?
解:设如果每行站16人,能站 x 行。
每行的人数×行数=总人数(一定),每行的人数和行数成反比例。
16 x = 20×12
16 x = 240
x = 15
答:如果每行站16人,能站15行。
小试牛刀
3.
学校计划用方砖铺微机室地面,如果用边长5分米的方砖,需要用360块;如果改用边长6分米的方砖,需要多少块?
解:设如果改用边长6分米的,需要 x 块。
每块方砖的面积×块数=地面面积(一定)
6×6× x = 5×5×360
36 x = 9000
x = 250
答:如果改用边长6分米的,需要250块。
小试牛刀
4.
(1)明新骑车从甲地到乙地,前5分钟行了700米,照这样的速度,从甲地到乙地一共用了20分钟。甲、乙两地相距多少米?
路程
时间
= 速度(一定)
700
5
x
20
20
=
5 x = 14000
x = 2800
答:甲乙两地相距2800米。
解:甲乙两地相距 x 米。
小试牛刀
4.
解:返回时用了x 分钟。
(2)明新骑车从甲地到乙地一共用了20分钟,每分钟行140米;返回时每分钟行100米,返回时用了多少分钟?
速度×时间 = 路程(一定)
100× x = 140×20
100 x = 2800
答:返回时用了28分钟。
x = 28
小试牛刀
5.
解:设他的车模的速度是每分钟 x 米。
速度×时间 = 路程(一定)
学校举行四驱车模比赛。小强的车模速度为480米/分,跑完全程用了5分钟。小瑞的车模跑完全程比小强的多用了1分钟,他的车模速度是多少?
6 x = 2400
(5+1)x = 480×5
答:他的车模的速度是每分钟400米。
x = 400
课堂小结
4
用正比例知识解决问题的步骤:
(1)找量。找到两种相关联的量及不变的量;
(2)判断。判断两种相关联的量是否成正比例;
(3)列式求解。设未知数,列比例式并求解;
(4)检验并写出答语。
用反比例知识解决问题的步骤:
(1)找量。找到两种相关联的量及不变的量;
(2)判断。判断两种相关联的量是否成反比例;
(3)列式求解。设未知数,列方程并求解;
(4)检验并写出答语。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
