【班海精品】青岛版(2015)五下-第七单元 5.长方体和正方体的体积【优质课件】
文档属性
| 名称 | 【班海精品】青岛版(2015)五下-第七单元 5.长方体和正方体的体积【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 11:22:32 | ||
图片预览





文档简介
(共31张PPT)
长方体和
正方体的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
根据这些信息,你能提出什么问题?
从图中,你知道了哪些数学信息?
可乐箱的长、宽、
高分别是7dm、
3dm、2dm。
桃汁饮料盒的长、
宽、高分别是10cm、
7cm、20cm。
啤酒箱的长、宽、
高分别是3dm、
3dm、3dm。
怎样求可乐箱的体积呢?
桃汁饮料盒能盛多少升饮料?
啤酒箱的体积呢?
新课精讲
探索新知
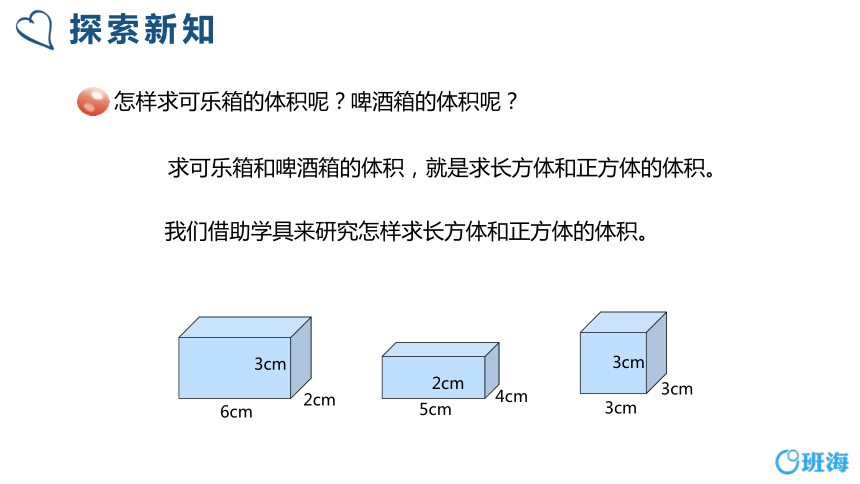
怎样求可乐箱的体积呢?啤酒箱的体积呢?
6cm
3cm
2cm
5cm
2cm
4cm
3cm
3cm
3cm
我们借助学具来研究怎样求长方体和正方体的体积。
求可乐箱和啤酒箱的体积,就是求长方体和正方体的体积。
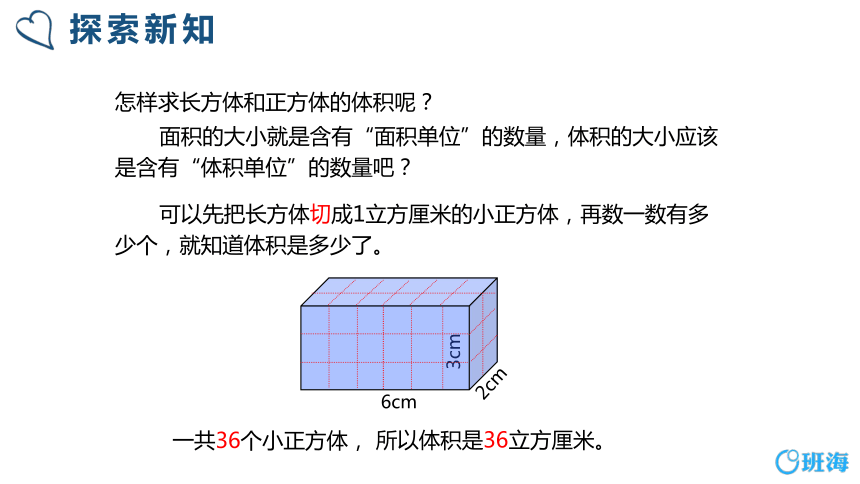
探索新知
一共36个小正方体,
2cm
6cm
3cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
所以体积是36立方厘米。
怎样求长方体和正方体的体积呢?
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧?
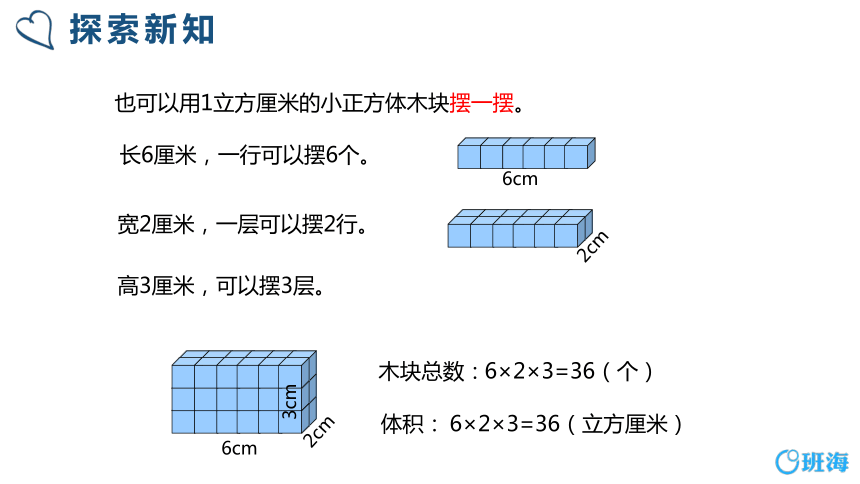
探索新知
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
高3厘米,可以摆3层。
木块总数:
6×2×3=36(个)
2cm
6cm
3cm
6cm
2cm
也可以用1立方厘米的小正方体木块摆一摆。
体积:
6×2×3=36(立方厘米)
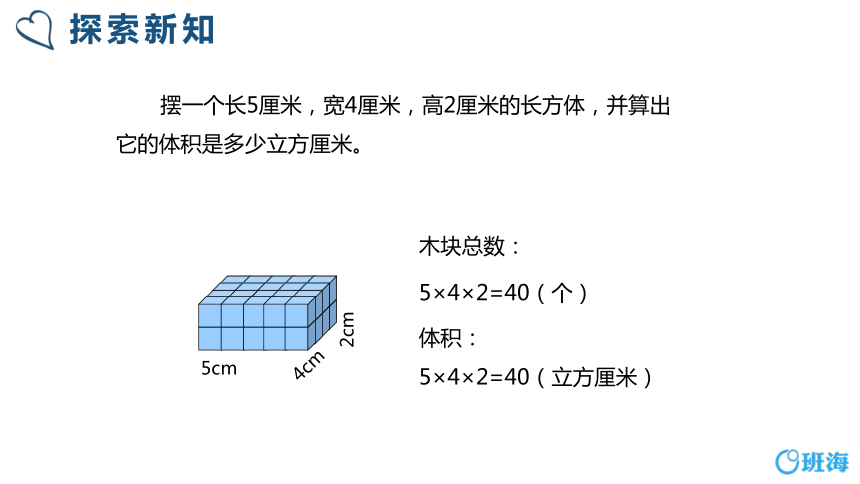
探索新知
4cm
5cm
2cm
木块总数:
5×4×2=40(个)
体积:
5×4×2=40(立方厘米)
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
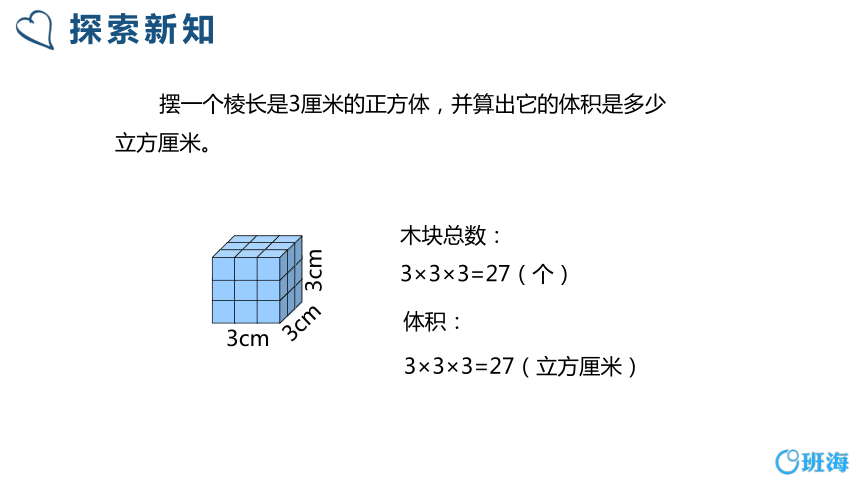
探索新知
3cm
3cm
3cm
木块总数:
3×3×3=27(个)
体积:
3×3×3=27(立方厘米)
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
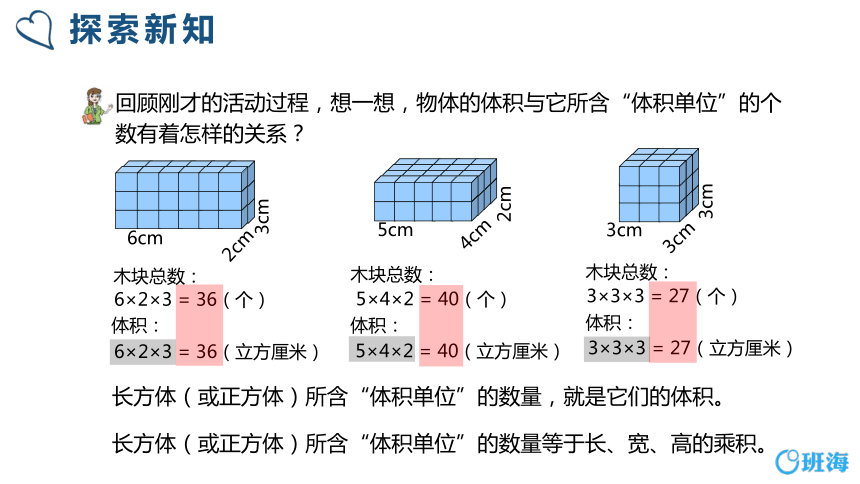
探索新知
2cm
6cm
3cm
木块总数:
6×2×3 = 36(个)
体积:
6×2×3 = 36(立方厘米)
体积:
5×4×2 = 40(立方厘米)
木块总数:
5×4×2 = 40(个)
4cm
5cm
2cm
3×3×3 = 27(立方厘米)
3cm
3cm
3cm
木块总数:
3×3×3 = 27(个)
体积:
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量等于长、宽、高的乘积。
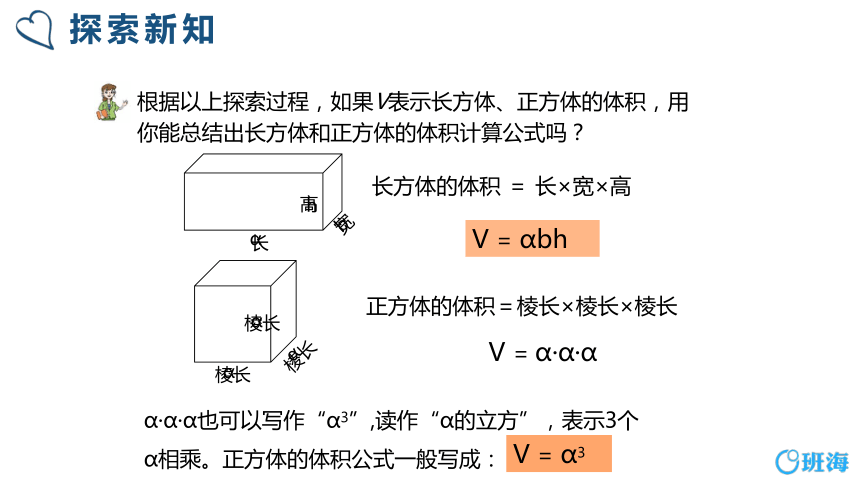
探索新知
b
ɑ
h
长方体的体积 = 长×宽×高
V = ɑbh
正方体的体积=棱长×棱长×棱长
V = ɑ·ɑ·ɑ
ɑ
ɑ
ɑ
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
长
宽
高
棱长
棱长
棱长
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
探索新知
b
ɑ
ɑ
ɑ
ɑ
h
底面
底面
长方体和正方体底面的面积叫作它们的底面积。
你能用同一个公式来表示长方体和正方体体积的计算方法吗?
长方体(或正方体)的体积 = 底面积×高
V = Sh
是不是所有立体图形的体积都等于底面积乘高呢?
探索新知
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
你会求可乐箱的体积了吗?
啤酒箱的体积呢?
答:可乐箱的体积是42 dm3 。
答:啤酒箱的体积是27 dm3 。
探索新知
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
10×7×20 = 1400(立方厘米)
1400立方厘米 = 1.4升
答:桃汁饮料盒能盛 1.4 升饮料。
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
盒壁厚度不计是什么意思?
探索新知
长方体体积不难算,长乘宽来再乘高。
正方体体积更简单,棱长立方立显现。
如果统一计算式,底面面积去乘高。
已知其中部分量,变形公式来解题。
计算公式掌握好,困难见它全逃跑。
典题精讲
1.填一填。
(1)长方体的体积与它的( )、( )、( )有关,如果用V表示体
积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积
计算公式是( )。
(2)如果用V表示体积,用a表示正方体的棱长,正方体的体积公式用字
母表示为( )。
(3)长方体(或正方体)的体积=( )×( )。
(4)棱长是6分米的正方体的体积是( )立方分米。
(5)一个长方体的体积是96立方分米,底面积是16平方分米,它的高
是( )分米。
长
宽
高
V=abh
V=a3
底面积
高
216
6
典题精讲
(6)容积的计算方法与( )的计算方法相同,但是数据要从
容器( )测量。
(7)冷藏车的车厢是长方体,从里面量,长4米,宽2.5米,高1.8
米,它的容积是( )立方米。
(8) 一个长方体铁皮水桶的高是6分米,底面是边长为3分米的正
方形,这个水桶的容积是( )升。(铁皮厚度不计)
(9)一个正方体油箱,从里面量棱长是5分米,每升汽油重0.8千克,
这个油箱可装汽油( )千克。
体积
里面
18
54
100
典题精讲
2.求下面各图形的体积。
1.2×0.4×0.6=0.288(立方米)
8×10×22=1760(dm3)
64×20=1280(cm3)
8×8×8=512(立方分米)
典题精讲
3.选一选。
(1)用棱长2厘米的小正方体拼成一个大正方体,大正方体的体
积可能是( )立方厘米。
A.32 B.24 C.64 D.16
(2)一个长方体的长、宽、高分别扩大到原来的2倍,它的体积
扩大到原来的( )倍。
A.6 B.8 C.9 D.27
C
B
典题精讲
(3)把一根长为2米的长方体木料锯成两段后,表面积增加了100平方厘米,原来长方体的体积是( )。
A.200立方厘米 B.10000立方厘米
C.2立方分米 D.20立方分米
B
(4)一个长方体的纸盒从里面量长6分米、宽4分米、高8分米,若把
棱长2分米的正方体积木装进木箱内(不外露),最多能装( )多块。
A.6 B.12 C.24 D.36
C
易错提醒
1.判断。
棱长6厘米的正方体,它的表面积和体积相等。( )
×
辨析:体积与面积概念混淆。
2.将一块体积2 dm3的长方体橡皮泥捏成正方体,它的体积是( )。
辨析:物体的体积与形状的关系。
2dm3
学以致用
小试牛刀
1.你知道它们的体积各是多少吗?
42
27
1cm3
1cm3
( )cm3
( )cm3
小试牛刀
2.计算下面图形的体积。
5×8×5=200(cm3)
4×4×4=64(dm3)
20×4×5=400(m3)
小试牛刀
3. 一段长3米的方木,横截面是一个边长0.2米的正方形。50根这样
的方木,体积是多少立方米?
0.2×0.2×3 = 0.12(立方米)
0.12×50 = 6(立方米)
答:50根这样的方木,体积是 6 立方米。
0.2米
3米
小试牛刀
4.右图是一瓶清洁剂。瓶的形状近似长方体,它长7.3厘米,宽4
厘米,高22厘米。这瓶清洁剂有多少毫升?(瓶壁厚度忽略不计)
7.3×4×22 = 642.4(立方厘米)
642.4立方厘米 = 642.4毫升
答:这瓶清洁剂有642.4 毫升。
小试牛刀
5.一个蓄水池,长10米,宽4米,深2米。
10×2×4 = 80(立方米)
10×4 = 40(平方米)
(1)蓄水池占地面积有多大?
(2)在蓄水池的底面和四周抹上水泥,
抹水泥的面积有多大?
(3)蓄水池最多能蓄水多少立方米?
10×4 +(4×2+2×10)×2= 96(平方米)
答:抹水泥的面积有96平方米。
答:蓄水池最多能蓄水80立方米。
答:蓄水池占地面积有40平方米。
课堂小结
归纳总结:
3.计算容器的容积,一般应从里面测量它的长、宽、高等数据,如果容器厚度可以忽略不计,也可以从外面量。
4.如果容器里盛放的是液体,还要注意进行单位换算,即把体积单位立方厘米、立方分米、立方米化成容积单位升或毫升。
1.长方体的体积=长×宽×高,用字母表示为:V=abh;
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a= ɑ3 。
2.长方体和正方体底面的面积叫作它们的底面积,
长方体(或正方体)的体积=底面积×高,V=Sh。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
长方体和
正方体的体积
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
根据这些信息,你能提出什么问题?
从图中,你知道了哪些数学信息?
可乐箱的长、宽、
高分别是7dm、
3dm、2dm。
桃汁饮料盒的长、
宽、高分别是10cm、
7cm、20cm。
啤酒箱的长、宽、
高分别是3dm、
3dm、3dm。
怎样求可乐箱的体积呢?
桃汁饮料盒能盛多少升饮料?
啤酒箱的体积呢?
新课精讲
探索新知
怎样求可乐箱的体积呢?啤酒箱的体积呢?
6cm
3cm
2cm
5cm
2cm
4cm
3cm
3cm
3cm
我们借助学具来研究怎样求长方体和正方体的体积。
求可乐箱和啤酒箱的体积,就是求长方体和正方体的体积。
探索新知
一共36个小正方体,
2cm
6cm
3cm
可以先把长方体切成1立方厘米的小正方体,再数一数有多少个,就知道体积是多少了。
所以体积是36立方厘米。
怎样求长方体和正方体的体积呢?
面积的大小就是含有“面积单位”的数量,体积的大小应该是含有“体积单位”的数量吧?
探索新知
长6厘米,一行可以摆6个。
宽2厘米,一层可以摆2行。
高3厘米,可以摆3层。
木块总数:
6×2×3=36(个)
2cm
6cm
3cm
6cm
2cm
也可以用1立方厘米的小正方体木块摆一摆。
体积:
6×2×3=36(立方厘米)
探索新知
4cm
5cm
2cm
木块总数:
5×4×2=40(个)
体积:
5×4×2=40(立方厘米)
摆一个长5厘米,宽4厘米,高2厘米的长方体,并算出它的体积是多少立方厘米。
探索新知
3cm
3cm
3cm
木块总数:
3×3×3=27(个)
体积:
3×3×3=27(立方厘米)
摆一个棱长是3厘米的正方体,并算出它的体积是多少立方厘米。
探索新知
2cm
6cm
3cm
木块总数:
6×2×3 = 36(个)
体积:
6×2×3 = 36(立方厘米)
体积:
5×4×2 = 40(立方厘米)
木块总数:
5×4×2 = 40(个)
4cm
5cm
2cm
3×3×3 = 27(立方厘米)
3cm
3cm
3cm
木块总数:
3×3×3 = 27(个)
体积:
回顾刚才的活动过程,想一想,物体的体积与它所含“体积单位”的个数有着怎样的关系?
长方体(或正方体)所含“体积单位”的数量,就是它们的体积。
长方体(或正方体)所含“体积单位”的数量等于长、宽、高的乘积。
探索新知
b
ɑ
h
长方体的体积 = 长×宽×高
V = ɑbh
正方体的体积=棱长×棱长×棱长
V = ɑ·ɑ·ɑ
ɑ
ɑ
ɑ
根据以上探索过程,如果V表示长方体、正方体的体积,用你能总结出长方体和正方体的体积计算公式吗?
长
宽
高
棱长
棱长
棱长
ɑ·ɑ·ɑ也可以写作“ɑ3”,读作“ɑ的立方”,表示3个ɑ相乘。正方体的体积公式一般写成:
V = ɑ3
探索新知
b
ɑ
ɑ
ɑ
ɑ
h
底面
底面
长方体和正方体底面的面积叫作它们的底面积。
你能用同一个公式来表示长方体和正方体体积的计算方法吗?
长方体(或正方体)的体积 = 底面积×高
V = Sh
是不是所有立体图形的体积都等于底面积乘高呢?
探索新知
可乐箱的体积:
7×3×2 = 42(dm3)
啤酒箱的体积:
3×3×3 = 27(dm3)
你会求可乐箱的体积了吗?
啤酒箱的体积呢?
答:可乐箱的体积是42 dm3 。
答:啤酒箱的体积是27 dm3 。
探索新知
桃汁饮料盒能盛多少升饮料?(盒壁厚度不计)
长方体或正方体容器容积的计算方法与体积的计算方法相同,但要从容器里面量长、宽、高。
10×7×20 = 1400(立方厘米)
1400立方厘米 = 1.4升
答:桃汁饮料盒能盛 1.4 升饮料。
求桃汁饮料盒能盛多少升饮料,实际上就是求饮料盒的容积是多少。
盒壁厚度不计是什么意思?
探索新知
长方体体积不难算,长乘宽来再乘高。
正方体体积更简单,棱长立方立显现。
如果统一计算式,底面面积去乘高。
已知其中部分量,变形公式来解题。
计算公式掌握好,困难见它全逃跑。
典题精讲
1.填一填。
(1)长方体的体积与它的( )、( )、( )有关,如果用V表示体
积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积
计算公式是( )。
(2)如果用V表示体积,用a表示正方体的棱长,正方体的体积公式用字
母表示为( )。
(3)长方体(或正方体)的体积=( )×( )。
(4)棱长是6分米的正方体的体积是( )立方分米。
(5)一个长方体的体积是96立方分米,底面积是16平方分米,它的高
是( )分米。
长
宽
高
V=abh
V=a3
底面积
高
216
6
典题精讲
(6)容积的计算方法与( )的计算方法相同,但是数据要从
容器( )测量。
(7)冷藏车的车厢是长方体,从里面量,长4米,宽2.5米,高1.8
米,它的容积是( )立方米。
(8) 一个长方体铁皮水桶的高是6分米,底面是边长为3分米的正
方形,这个水桶的容积是( )升。(铁皮厚度不计)
(9)一个正方体油箱,从里面量棱长是5分米,每升汽油重0.8千克,
这个油箱可装汽油( )千克。
体积
里面
18
54
100
典题精讲
2.求下面各图形的体积。
1.2×0.4×0.6=0.288(立方米)
8×10×22=1760(dm3)
64×20=1280(cm3)
8×8×8=512(立方分米)
典题精讲
3.选一选。
(1)用棱长2厘米的小正方体拼成一个大正方体,大正方体的体
积可能是( )立方厘米。
A.32 B.24 C.64 D.16
(2)一个长方体的长、宽、高分别扩大到原来的2倍,它的体积
扩大到原来的( )倍。
A.6 B.8 C.9 D.27
C
B
典题精讲
(3)把一根长为2米的长方体木料锯成两段后,表面积增加了100平方厘米,原来长方体的体积是( )。
A.200立方厘米 B.10000立方厘米
C.2立方分米 D.20立方分米
B
(4)一个长方体的纸盒从里面量长6分米、宽4分米、高8分米,若把
棱长2分米的正方体积木装进木箱内(不外露),最多能装( )多块。
A.6 B.12 C.24 D.36
C
易错提醒
1.判断。
棱长6厘米的正方体,它的表面积和体积相等。( )
×
辨析:体积与面积概念混淆。
2.将一块体积2 dm3的长方体橡皮泥捏成正方体,它的体积是( )。
辨析:物体的体积与形状的关系。
2dm3
学以致用
小试牛刀
1.你知道它们的体积各是多少吗?
42
27
1cm3
1cm3
( )cm3
( )cm3
小试牛刀
2.计算下面图形的体积。
5×8×5=200(cm3)
4×4×4=64(dm3)
20×4×5=400(m3)
小试牛刀
3. 一段长3米的方木,横截面是一个边长0.2米的正方形。50根这样
的方木,体积是多少立方米?
0.2×0.2×3 = 0.12(立方米)
0.12×50 = 6(立方米)
答:50根这样的方木,体积是 6 立方米。
0.2米
3米
小试牛刀
4.右图是一瓶清洁剂。瓶的形状近似长方体,它长7.3厘米,宽4
厘米,高22厘米。这瓶清洁剂有多少毫升?(瓶壁厚度忽略不计)
7.3×4×22 = 642.4(立方厘米)
642.4立方厘米 = 642.4毫升
答:这瓶清洁剂有642.4 毫升。
小试牛刀
5.一个蓄水池,长10米,宽4米,深2米。
10×2×4 = 80(立方米)
10×4 = 40(平方米)
(1)蓄水池占地面积有多大?
(2)在蓄水池的底面和四周抹上水泥,
抹水泥的面积有多大?
(3)蓄水池最多能蓄水多少立方米?
10×4 +(4×2+2×10)×2= 96(平方米)
答:抹水泥的面积有96平方米。
答:蓄水池最多能蓄水80立方米。
答:蓄水池占地面积有40平方米。
课堂小结
归纳总结:
3.计算容器的容积,一般应从里面测量它的长、宽、高等数据,如果容器厚度可以忽略不计,也可以从外面量。
4.如果容器里盛放的是液体,还要注意进行单位换算,即把体积单位立方厘米、立方分米、立方米化成容积单位升或毫升。
1.长方体的体积=长×宽×高,用字母表示为:V=abh;
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a= ɑ3 。
2.长方体和正方体底面的面积叫作它们的底面积,
长方体(或正方体)的体积=底面积×高,V=Sh。
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
