【班海精品】青岛版(2015)四下-第三单元 3.乘法分配律【优质课件】
文档属性
| 名称 | 【班海精品】青岛版(2015)四下-第三单元 3.乘法分配律【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 11:22:45 | ||
图片预览









文档简介
(共31张PPT)
乘法分配律
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
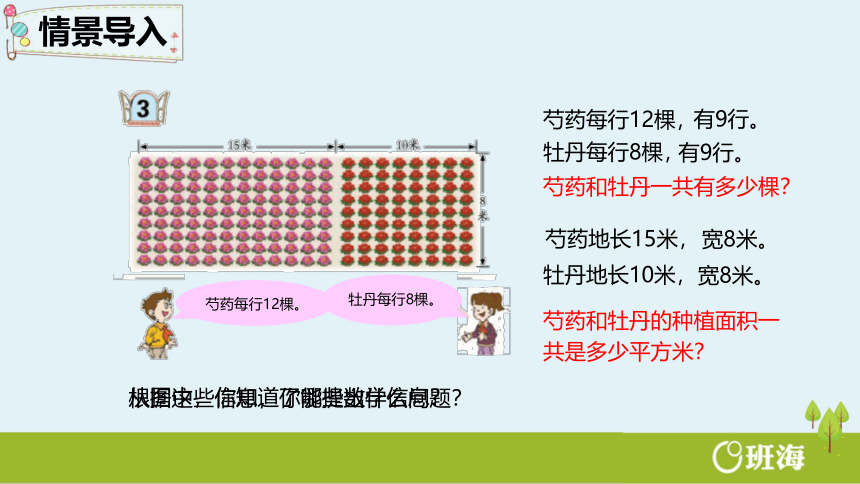
情景导入
从图中,你知道了哪些数学信息?
有9行。
根据这些信息,你能提出什么问题?
牡丹每行8棵。
芍药每行12棵。
芍药每行12棵,
芍药和牡丹一共有多少棵?
牡丹每行8棵,
有9行。
芍药地长15米,
牡丹地长10米,
芍药和牡丹的种植面积一共是多少平方米?
宽8米。
宽8米。
新课精讲
探索新知
芍药和牡丹一共多少棵?
想一想:
1.要解决这个问题,可以先求什么,再求什么?
2.你会列综合算式解答吗?
探索新知
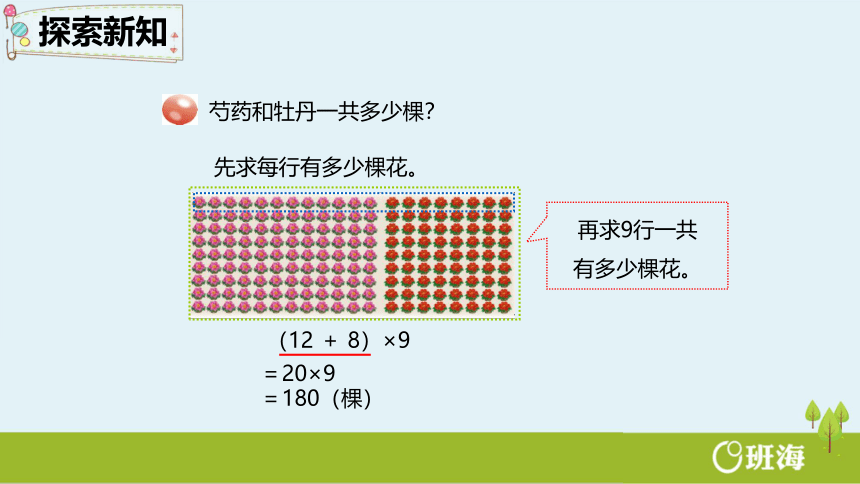
(12 + 8)×9
芍药和牡丹一共多少棵?
=180(棵)
=20×9
先求每行有多少棵花。
再求9行一共
有多少棵花。
探索新知
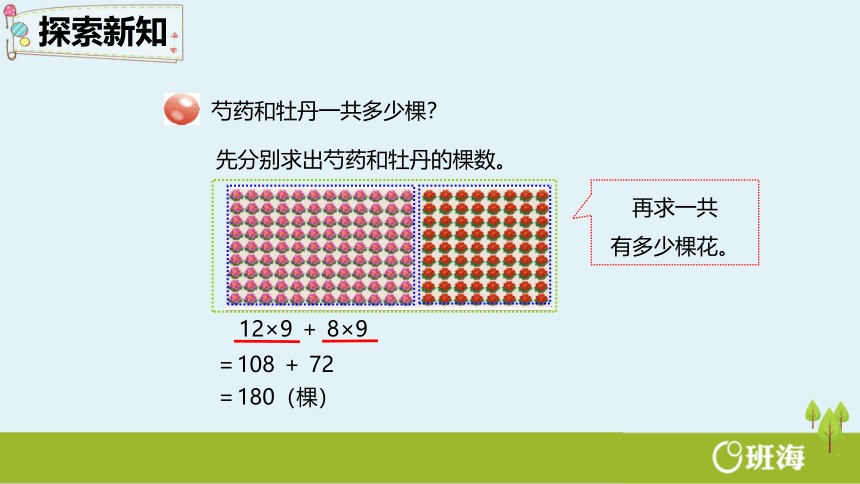
芍药和牡丹一共多少棵?
先分别求出芍药和牡丹的棵数。
再求一共
有多少棵花。
12×9 + 8×9
=180(棵)
=108 + 72
探索新知
比较两种解答方法,你发现了什么?
(12 + 8)×9
= 20×9
= 180(棵)
你能把这两道算式写成一个等式吗?
(12+8)×9 = 12×9+8×9
12×9 + 8×9
= 108 + 72
= 180(棵)
探索新知
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
(15+10)×8 =15×8+10×8
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探索新知
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
15×8+10×8
(15+10)×8
=
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探索新知
15×8+10×8
(15+10)×8 =
12×9+8×9
(12+8)×9 =
观察下面两组算式,你发现了什么?
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
这是不是一个规律呢?
探索新知
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加 这个规律叫作乘法分配律。
通过验证,你得出了什么结论?
能举例验证一下吗?你想怎样验证?
探索活动要求
3.如果数据较大,计算时可以使用计算器。
2.为确保结论的可靠性,举例验证时,较大数、较小数及特殊数(如1、0等)的例子都要有。
1.在验证卡的横线上写出两组算式。
探索新知
乘法分配律能用字母表示吗?
(12+ 8 )× 9 = 12 × 9 + 8 × 9
+
=
你知道为什么可以这样表示吗?
(15+10)× 8 = 15 × 8 +10× 8
ɑ
c
+
b
( )
·
ɑ
·
c
b
·
c
探索新知
(2+4)×3= 2×3 +4×3
3
5
4
(3+5)×4= 3×4 +5×4
行与列各增加1排,你还能用算式表示吗?
你能用算式表示一共有多少个圆片吗?
探索新知
(3+5)×4=3×4+5×4
4
6
5
(4+6)×5=4×5+6×5
(2+4)×3=2×3 +4×3
探索新知
(3+5)×4=3×4+5×4
(4+6)×5=4×5+6×5
(2+4)×3=2×3+4×3
探索新知
a
c
b
(ɑ +b )·c=ɑ·c+b·c
(3+5)×4=3×4+5×4
(4+6)×5=4×5+6×5
(2+4)×3=2×3+4×3
探索新知
运用乘法分配律能使运算结果简便吗?
135×6 + 65×6
=(135+65)×6
= 200×6
= 1200
12×105
= 12×(100+5)
= 12×100+12×5
= 1260
135×6+65×6
12×105
典型例题
1. 不计算,在 里填上“>”“<”或“=”,并填空。
(15+28)×6 15×6+28×6
20×(17+35) 20×17+35×20
由以上结果,可发现两个数的和乘一个数,可以把它们分别乘这个数,再把所得的积相加,这个规律叫作( ),用字母表示为( )。
=
=
乘法分配律
(a+b) c=a c+b c
典型例题
2、填一填。
1.45×a+a×55=(____+____)×a
2.(a+b) c=______+______
3.____×(____+____)=25×15+25×5
4.18×(____+____)=____×5+____×3
以上四个等式的依据是 ( )律。
45
55
a c
b c
25
15
5
5
3
18
18
乘法分配
典型例题
3、连一连。
(35+65)×x 7×(25×4)
7×25×4 35×x+65×x
36×b (c+b)×34
c×34+b×34 b×36
判断对错,错的请改正。
(1)(25+36)×4 改正:
=25×4+36
=100+36
=136 ( )
(2)68×101 改正:
=68×100+1
=6800+1
=6801 ( )
×
(25+36)×4
=25×4+36×4
=100+144
=244
68×101
=68×100+68
=6800+68
=6868
×
易错提醒
(3)89×99+89 改正:
=89×100+89
=8900+89
=8989 ( )
×
89×99+89
=89×(99+1)
=89×100
=8900
辨析:正确运用乘法分配律进行简算。
易错提醒
学以致用
小试牛刀
① 236×3+236×7= ×( + )
②(125 + 60)× = 125×8 + 60×8
1.想一想,做一做。
8
236
3
7
2、用简便方法计算。
37×9+9×63 25×(10+4)
(25+8)×40 32×65+32×35
=(37+63)×9
=100×9
=900
=25×10+25×4
=250+100
=350
=25×40+8×40
=1000+320
=1320
=32×(65+35)
=32×100
=3200
小试牛刀
小试牛刀
3.
(1)这列火车最多能乘坐多少乘客?
(2)你还能提出什么问题?
102×12+98×12
= 200 ×12
= 2400 (人)
(102+98)×12
= 102×12+ 98×12
= 1224+ 1176
= 2400 (人)
课堂小结
归纳总结:
乘法分配律:
两个数的和与一个数相乘等于这两个数分别与这个数相乘,再把所得的积相加。用字母表示为:(a+b)·c=a·c+b·c。
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
乘法分配律
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
从图中,你知道了哪些数学信息?
有9行。
根据这些信息,你能提出什么问题?
牡丹每行8棵。
芍药每行12棵。
芍药每行12棵,
芍药和牡丹一共有多少棵?
牡丹每行8棵,
有9行。
芍药地长15米,
牡丹地长10米,
芍药和牡丹的种植面积一共是多少平方米?
宽8米。
宽8米。
新课精讲
探索新知
芍药和牡丹一共多少棵?
想一想:
1.要解决这个问题,可以先求什么,再求什么?
2.你会列综合算式解答吗?
探索新知
(12 + 8)×9
芍药和牡丹一共多少棵?
=180(棵)
=20×9
先求每行有多少棵花。
再求9行一共
有多少棵花。
探索新知
芍药和牡丹一共多少棵?
先分别求出芍药和牡丹的棵数。
再求一共
有多少棵花。
12×9 + 8×9
=180(棵)
=108 + 72
探索新知
比较两种解答方法,你发现了什么?
(12 + 8)×9
= 20×9
= 180(棵)
你能把这两道算式写成一个等式吗?
(12+8)×9 = 12×9+8×9
12×9 + 8×9
= 108 + 72
= 180(棵)
探索新知
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
(15+10)×8 =15×8+10×8
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探索新知
芍药和牡丹的种植面积一共是多少平方米?
(15 + 10)×8
15×8 + 10×8
15×8+10×8
(15+10)×8
=
你能把这两道算式写成一个等式吗?
= 120 + 80
= 200(平方米)
= 25 ×8
= 200(平方米)
探索新知
15×8+10×8
(15+10)×8 =
12×9+8×9
(12+8)×9 =
观察下面两组算式,你发现了什么?
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
这是不是一个规律呢?
探索新知
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加 这个规律叫作乘法分配律。
通过验证,你得出了什么结论?
能举例验证一下吗?你想怎样验证?
探索活动要求
3.如果数据较大,计算时可以使用计算器。
2.为确保结论的可靠性,举例验证时,较大数、较小数及特殊数(如1、0等)的例子都要有。
1.在验证卡的横线上写出两组算式。
探索新知
乘法分配律能用字母表示吗?
(12+ 8 )× 9 = 12 × 9 + 8 × 9
+
=
你知道为什么可以这样表示吗?
(15+10)× 8 = 15 × 8 +10× 8
ɑ
c
+
b
( )
·
ɑ
·
c
b
·
c
探索新知
(2+4)×3= 2×3 +4×3
3
5
4
(3+5)×4= 3×4 +5×4
行与列各增加1排,你还能用算式表示吗?
你能用算式表示一共有多少个圆片吗?
探索新知
(3+5)×4=3×4+5×4
4
6
5
(4+6)×5=4×5+6×5
(2+4)×3=2×3 +4×3
探索新知
(3+5)×4=3×4+5×4
(4+6)×5=4×5+6×5
(2+4)×3=2×3+4×3
探索新知
a
c
b
(ɑ +b )·c=ɑ·c+b·c
(3+5)×4=3×4+5×4
(4+6)×5=4×5+6×5
(2+4)×3=2×3+4×3
探索新知
运用乘法分配律能使运算结果简便吗?
135×6 + 65×6
=(135+65)×6
= 200×6
= 1200
12×105
= 12×(100+5)
= 12×100+12×5
= 1260
135×6+65×6
12×105
典型例题
1. 不计算,在 里填上“>”“<”或“=”,并填空。
(15+28)×6 15×6+28×6
20×(17+35) 20×17+35×20
由以上结果,可发现两个数的和乘一个数,可以把它们分别乘这个数,再把所得的积相加,这个规律叫作( ),用字母表示为( )。
=
=
乘法分配律
(a+b) c=a c+b c
典型例题
2、填一填。
1.45×a+a×55=(____+____)×a
2.(a+b) c=______+______
3.____×(____+____)=25×15+25×5
4.18×(____+____)=____×5+____×3
以上四个等式的依据是 ( )律。
45
55
a c
b c
25
15
5
5
3
18
18
乘法分配
典型例题
3、连一连。
(35+65)×x 7×(25×4)
7×25×4 35×x+65×x
36×b (c+b)×34
c×34+b×34 b×36
判断对错,错的请改正。
(1)(25+36)×4 改正:
=25×4+36
=100+36
=136 ( )
(2)68×101 改正:
=68×100+1
=6800+1
=6801 ( )
×
(25+36)×4
=25×4+36×4
=100+144
=244
68×101
=68×100+68
=6800+68
=6868
×
易错提醒
(3)89×99+89 改正:
=89×100+89
=8900+89
=8989 ( )
×
89×99+89
=89×(99+1)
=89×100
=8900
辨析:正确运用乘法分配律进行简算。
易错提醒
学以致用
小试牛刀
① 236×3+236×7= ×( + )
②(125 + 60)× = 125×8 + 60×8
1.想一想,做一做。
8
236
3
7
2、用简便方法计算。
37×9+9×63 25×(10+4)
(25+8)×40 32×65+32×35
=(37+63)×9
=100×9
=900
=25×10+25×4
=250+100
=350
=25×40+8×40
=1000+320
=1320
=32×(65+35)
=32×100
=3200
小试牛刀
小试牛刀
3.
(1)这列火车最多能乘坐多少乘客?
(2)你还能提出什么问题?
102×12+98×12
= 200 ×12
= 2400 (人)
(102+98)×12
= 102×12+ 98×12
= 1224+ 1176
= 2400 (人)
课堂小结
归纳总结:
乘法分配律:
两个数的和与一个数相乘等于这两个数分别与这个数相乘,再把所得的积相加。用字母表示为:(a+b)·c=a·c+b·c。
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
