【班海精品】苏教版(新)五下-第六单元 7.1解决问题的策略(一)【优质课件】
文档属性
| 名称 | 【班海精品】苏教版(新)五下-第六单元 7.1解决问题的策略(一)【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
解决问题的策略(一)
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
请欣赏下面,生活中的错觉图片。
02
新课精讲
探索新知
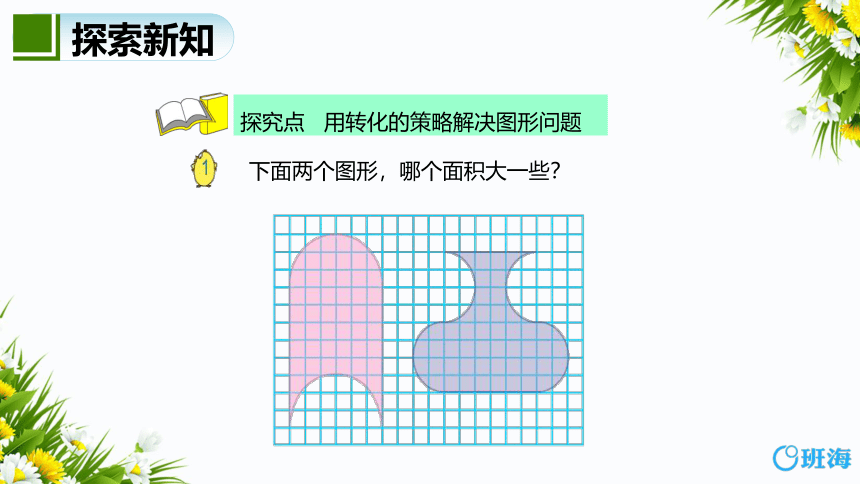
下面两个图形,哪个面积大一些?
探究点 用转化的策略解决图形问题
探索新知
可以数方格比较它们的面积。
把它们转化成规则图形进行比较。
你打算怎样比较这两个图形的面积?
探索新知
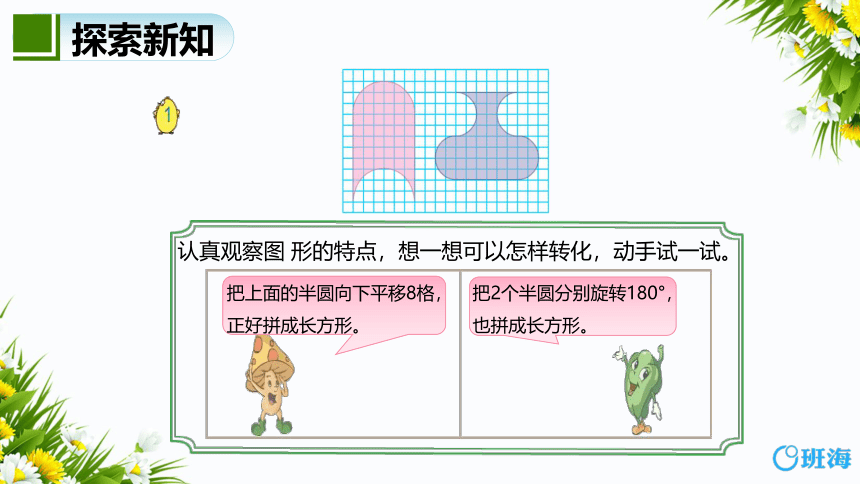
把2个半圆分别旋转180°,也拼成长方形。
把上面的半圆向下平移8格,正好拼成长方形。
认真观察图 形的特点,想一想可以怎样转化,动手试一试。
探索新知
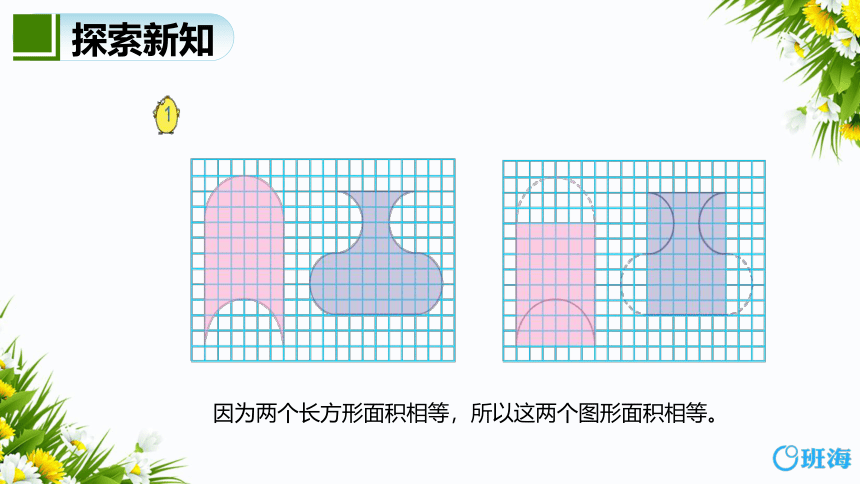
因为两个长方形面积相等,所以这两个图形面积相等。
探索新知
回顾解决问题的过程,你有什么体会?
图形转化时可以运用平移、旋转等方法。
有些不规则的图形可以转化成熟悉的简单的图形。
转化后的图形与转化前相比,形状变了,大小没有变。
探索新知
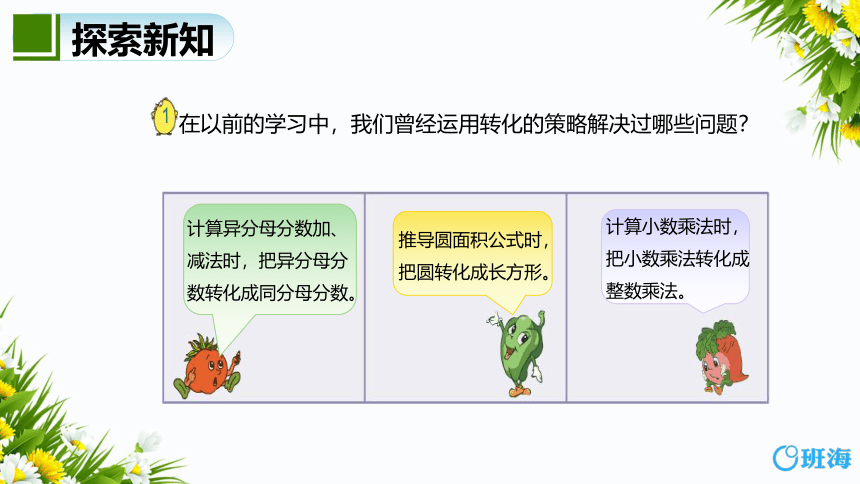
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
探索新知
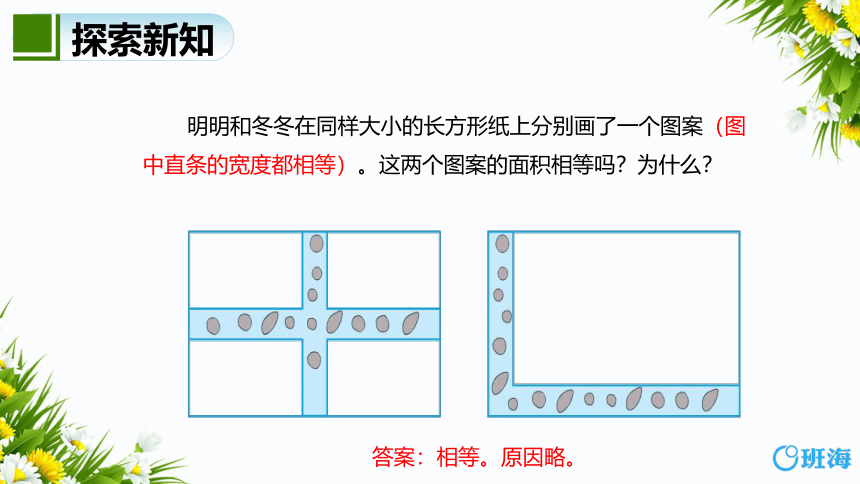
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
答案:相等。原因略。
典题精讲
1. 下面的两个图形,哪个面积大一些?
答:两个图形的面积一样大。
典题精讲
2. 小林和小军在同样大小的正方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
答:相等,因为左图中的两个平行四边形可以转化成右图中的两个长方形。
典题精讲
3. 用分数表示下列各图中的涂色部分。
1
4
1
4
17
25
典题精讲
4.观察下面的两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
转化成长方形,求长方形的周长比较简便。
(6+4)×2=20(厘米)
答:右边图形的周长是20厘米。
易错提醒
在一个长15米,宽12米的菜地中间有两条宽1米的小路,求小路的面积。
15×1+12×1-1×1=26(平方米)
答:小路的面积是26平方米。
易错点:忽略重合部分的面积。
03
学以致用
小试牛刀
1.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
将右边图形中的某些线经过平移可以得到左边图形,所以它的周长与左边图形的周长相等,为(5+3)×2=16(厘米)。
小试牛刀
2.用分数表示各图中的涂色部分。
1
4
1
2
1
8
小试牛刀
3.一块草坪倍4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
(45-2)×(27-2)=1075(平方米)
把小路平移到左边或下边计算比较简便。
小试牛刀
4.计算下面各图的周长。
1×4=4(m)
3.14×4+3.14×4=25.12(cm)
小试牛刀
5.
相等。因为经过旋转和平移,可以把左边图形变成右边图形。
小试牛刀
6.求涂色部分的面积。(单位:cm)
(1)3.14×(4÷2)2+4×4-3.14×(4÷2)2=16(cm2)
(2)涂色部分的面积可看成一个三角形的面积:
2
1
×12×12=72(cm )
(1)
(2)
小试牛刀
7.明光小学有一个花坛(如下图)。图中正方形的边长为10米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。
花坛可看成由一个正方形和3个相等的圆组成的。
10×10+3.14×32×3=184.78(平方米)
小试牛刀
8.
左图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
整个图形的周长等于两个涂色正方形周长的和。
(40÷4) =100(平方厘米)
小试牛刀
(27+19)×2=92(cm)
9.
04
课堂小结
用转化的策略解决面积问题:
运用转化策略可以把不规则的图形转化成规则的图形,转化后的图形与转化前的图形相比,形状变了,大小不变。
归纳总结:
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
解决问题的策略(一)
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目 录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
请欣赏下面,生活中的错觉图片。
02
新课精讲
探索新知
下面两个图形,哪个面积大一些?
探究点 用转化的策略解决图形问题
探索新知
可以数方格比较它们的面积。
把它们转化成规则图形进行比较。
你打算怎样比较这两个图形的面积?
探索新知
把2个半圆分别旋转180°,也拼成长方形。
把上面的半圆向下平移8格,正好拼成长方形。
认真观察图 形的特点,想一想可以怎样转化,动手试一试。
探索新知
因为两个长方形面积相等,所以这两个图形面积相等。
探索新知
回顾解决问题的过程,你有什么体会?
图形转化时可以运用平移、旋转等方法。
有些不规则的图形可以转化成熟悉的简单的图形。
转化后的图形与转化前相比,形状变了,大小没有变。
探索新知
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
推导圆面积公式时,把圆转化成长方形。
计算小数乘法时,把小数乘法转化成整数乘法。
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
探索新知
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
答案:相等。原因略。
典题精讲
1. 下面的两个图形,哪个面积大一些?
答:两个图形的面积一样大。
典题精讲
2. 小林和小军在同样大小的正方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
答:相等,因为左图中的两个平行四边形可以转化成右图中的两个长方形。
典题精讲
3. 用分数表示下列各图中的涂色部分。
1
4
1
4
17
25
典题精讲
4.观察下面的两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
转化成长方形,求长方形的周长比较简便。
(6+4)×2=20(厘米)
答:右边图形的周长是20厘米。
易错提醒
在一个长15米,宽12米的菜地中间有两条宽1米的小路,求小路的面积。
15×1+12×1-1×1=26(平方米)
答:小路的面积是26平方米。
易错点:忽略重合部分的面积。
03
学以致用
小试牛刀
1.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
将右边图形中的某些线经过平移可以得到左边图形,所以它的周长与左边图形的周长相等,为(5+3)×2=16(厘米)。
小试牛刀
2.用分数表示各图中的涂色部分。
1
4
1
2
1
8
小试牛刀
3.一块草坪倍4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米?
(45-2)×(27-2)=1075(平方米)
把小路平移到左边或下边计算比较简便。
小试牛刀
4.计算下面各图的周长。
1×4=4(m)
3.14×4+3.14×4=25.12(cm)
小试牛刀
5.
相等。因为经过旋转和平移,可以把左边图形变成右边图形。
小试牛刀
6.求涂色部分的面积。(单位:cm)
(1)3.14×(4÷2)2+4×4-3.14×(4÷2)2=16(cm2)
(2)涂色部分的面积可看成一个三角形的面积:
2
1
×12×12=72(cm )
(1)
(2)
小试牛刀
7.明光小学有一个花坛(如下图)。图中正方形的边长为10米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。
花坛可看成由一个正方形和3个相等的圆组成的。
10×10+3.14×32×3=184.78(平方米)
小试牛刀
8.
左图中两个涂色正方形周长的和是40厘米,求整个图形的面积。
整个图形的周长等于两个涂色正方形周长的和。
(40÷4) =100(平方厘米)
小试牛刀
(27+19)×2=92(cm)
9.
04
课堂小结
用转化的策略解决面积问题:
运用转化策略可以把不规则的图形转化成规则的图形,转化后的图形与转化前的图形相比,形状变了,大小不变。
归纳总结:
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
