第二节直角三角形练习(有答案)

北师版数学八年级下册第一章三角形的证明
第二节直角三角形练习
　
一．选择题（共9小题）
1．（2013 西宁）使两个直角三角形全等的条件是（　　）
　 A．一个锐角对应相等 B． 两个锐角对应相等
　 C．一条边对应相等 D． 两条边对应相等
2．（2009 江西）如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）
　 A． CB=CD B． ∠BAC=∠DAC C． ∠BCA=∠DCA D． ∠B=∠D=90°
3．在△ABC和△DEF中，∠A=∠D=90°，则下列条件中不能判定△ABC和△DEF全等的是（　　）
A． AB=DE，AC=DF B． AC=EF，BC=DF
C． AB=DE，BC=EF D． ∠C=∠F，BC=EF
4．如果两个直角三角形的两条直角边对应相等，那么这两个直角三角形全等的依据是（　　）
　 A． SSS B． AAS C． SAS D． HL
5．（2013 铁岭）如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（　　）
A． BC=EC，∠B=∠E B． BC=EC，AC=DC
C． BC=DC，∠A=∠D D． ∠B=∠E，∠A=∠D
6．（2013 台州）已知△A1B1C1，△A2B2C2的周长相等，现有两个判断：
①若A1B1=A2B2，A1C1=A2C2，则△A1B1C1≌△A2B2C2；
②若∠A1=∠A2，∠B1=∠B2，则△A1B1C1≌△A2B2C2，
对于上述的两个判断，下列说法正确的是（　　）
A． ①正确，②错误 B． ①错误，②正确 C． ①，②都错误 D． ①，②都正确
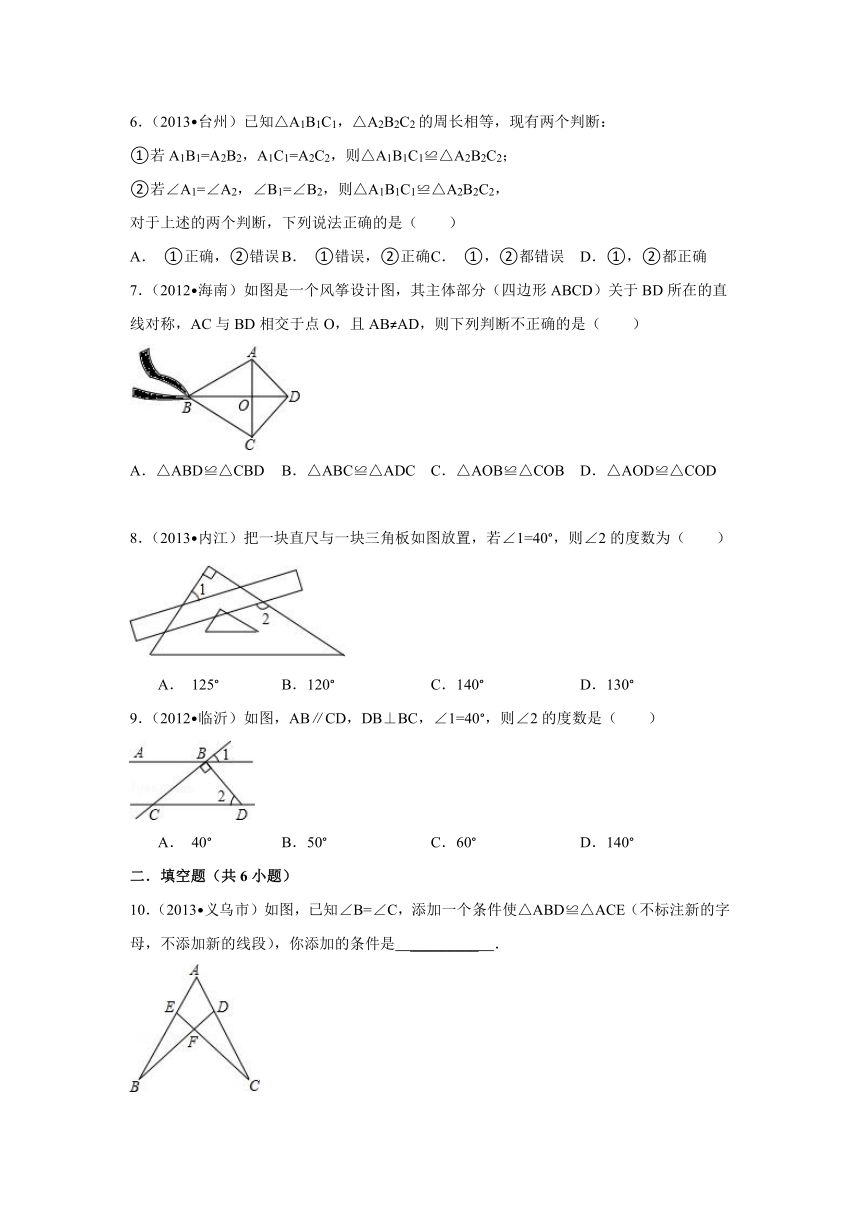
7．（2012 海南）如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD相交于点O，且AB≠AD，则下列判断不正确的是（　　）
A．△ABD≌△CBD B．△ABC≌△ADC C．△AOB≌△COB D． △AOD≌△COD
　
8．（2013 内江）把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（　　）
　 A． 125° B． 120° C． 140° D． 130°
9．（2012 临沂）如图，AB∥CD，DB⊥BC，∠1=40°，则∠2的度数是（　　）
　 A． 40° B． 50° C． 60° D． 140°
二．填空题（共6小题）
10．（2013 义乌市）如图，已知∠B=∠C，添加一个条件使△ABD≌△ACE（不标注新的字母，不添加新的线段），你添加的条件是　_________　．
11．（2013 天津）如图，已知∠C=∠D，∠ABC=∠BAD，AC与BD相交于点O，请写出图中一组相等的线段　_________　．
12．如图，AC⊥BC，AD⊥DB，要使△ABC≌△BAD，还需添加条件　_________　．（只需写出符合条件一种情况）
13．如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，线段PQ=AB，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP=　_________　时，△ABC和△PQA全等．
14．如图，∠A=∠D=90°，再添加一个条件　_________　，即可使Rt△ABC≌Rt△DCB，理由是　_________　．
15．如图，AB⊥CF，垂足为B，AB∥DE，点E在CF上，CE=FB，AC=DF，依据以上条件可以判定△ABC≌△DEF，这种判定三角形全等的方法，可以简写为　_________　．
　
三．解答题（共7小题）
16．（2012 肇庆）如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
求证：（1）BC=AD；
（2）△OAB是等腰三角形．
　
17．如图，点C在BE上，AB⊥BE，DE⊥BE，且AB=BE，BC=DE，AC交BD于F．
（1）求证：△ABC≌△BED；
（2）求∠BFC的度数．
　
18．如图，已知CE⊥AB，DF⊥AB，AC=BD，CE=DF，求证：AC∥BD．
　
19．如图，在△ABC中，AC=BC，直线l经过顶点C，过A，B两点分别作l的垂线AE，BF，E，F为垂足．AE=CF，求证：∠ACB=90°．
　
20．如图，AC⊥BC，BD⊥AD，AC=BD．求证：∠ABC=∠BAD．
　
21．如图，∠A=∠B=90°，E是AB上的一点，且AE=BC，∠1=∠2．
（1）Rt△ADE与Rt△BEC全等吗？并说明理由；
（2）△CDE是不是直角三角形？并说明理由．
　
22．已知：如图，Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°试判断CF和EF的关系，并说明你的理由．
　
参考答案
一．选择题
1． D．2． C．3． B．4． C．5． C．6． D．7． B．8． D．9． B．
二．填空题（共6小题）
10． AB=AC．11． AC=BD（答案不唯一）．12．AC=BD或BC=AD或∠DAB=∠CBA或∠CAB=∠DBA13． 5或10．14． AB=CD，HL．15． HL．
三．解答题（共7小题）
16． 证明：（1）∵AC⊥BC，BD⊥AD，∴∠ADB=∠ACB=90°，
在Rt△ABC和Rt△BAD中，∵，∴Rt△ABC≌Rt△BAD（HL），∴BC=AD，
（2）∵Rt△ABC≌Rt△BAD，∴∠CAB=∠DBA，∴OA=OB，∴△OAB是等腰三角形．
17．（1）证明：∵AB⊥BE，DE⊥BE，∴∠ABC=∠BED=90°，
在△ABC和△BED中，∴△ABC≌△BED（SAS）；
（2）解：∵△ABC≌△BED，∴∠DBE=∠CAB，∵∠ABC=90°，∴∠CAB+∠ACB=90°．∴∠DBE+∠ACB=90°．∴在△BFC中，∠BFC=90°．
18．证明：∵CE⊥AB，DF⊥AB，∴∠CEA=∠DFB=90°．又∵AC=BD，CE=DF，∴Rt△ACE≌Rt△BDF（HL）．∴∠A=∠B，∴AC∥BD．
19．证明：如图，在Rt△ACE和Rt△CBF中，
，∴Rt△ACE≌Rt△CBF（HL），∴∠EAC=∠BCF，∵∠EAC+∠ACE=90°，∴∠ACE+∠BCF=90°，∴∠ACB=180°﹣90°=90°．
20．解：∵AC⊥BC，BD⊥AD，∴在Rt△ABC和Rt△BAD中，AC=BD，AB=BA，∴Rt△ABC≌Rt△BAD（HL）∴∠ABC=∠BAD．
21．解：（1）全等，理由是：∵∠1=∠2，∴DE=CE，∵∠A=∠B=90°，AE=BC，∴Rt△ADE≌Rt△BEC（HL）；
（2）是直角三角形，理由是：∵Rt△ADE≌Rt△BEC，∴∠3=∠4，∵∠3+∠5=90°，∴∠4+∠5=90°，∴∠DEC=90°，∴△CDE是直角三角形．
22．解：CF=EF，
理由是：连接AF，∵Rt△ABC≌Rt△ADE，∴CB=DE，AB=AD，在Rt△ADF和Rt△ABF中，∴Rt△ADF≌Rt△ABF，∴DF=BF，∵BC=DE，∴BC﹣BF=DE﹣DF，
即CF=EF．