数学人教A版(2019)必修第二册6.1平面向量的概念及表示(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.1平面向量的概念及表示(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-29 18:48:07 | ||
图片预览






文档简介
(共27张PPT)
平面向量及其应用
章前语
向量是近代数学中重要和基本概念之一,向量理论具有丰富的物理背景、深刻的数学内涵。向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥着重要作用。
本章我们将通过实际背景引入向量的概念,类比数的运算,学习向量的运算及性质,建立向量的运算体系。在此基础上,用向量的语言、方法表述和解决现实生活、数学和物理中的一些问题。
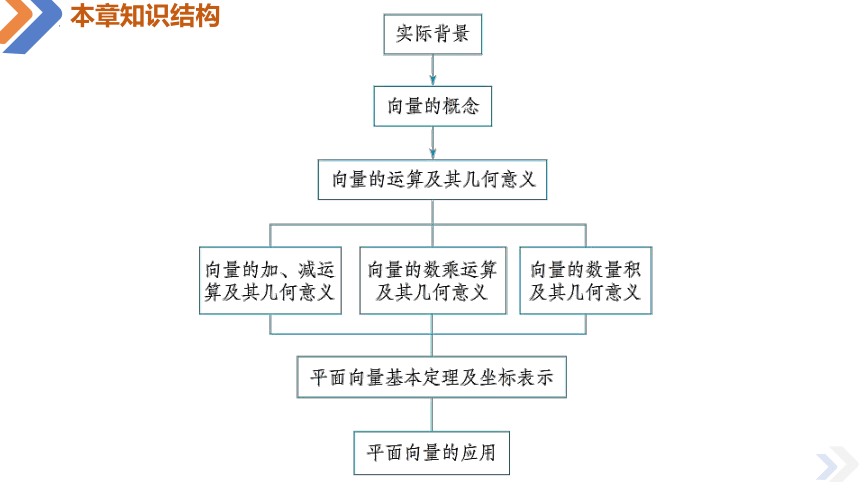
本章知识结构
平面向量的概念
§6.1
向量的实际背景与概念
向量的几何表示
相等向量与共线向量
小结及随堂练习
向量的实际背景与概念
01
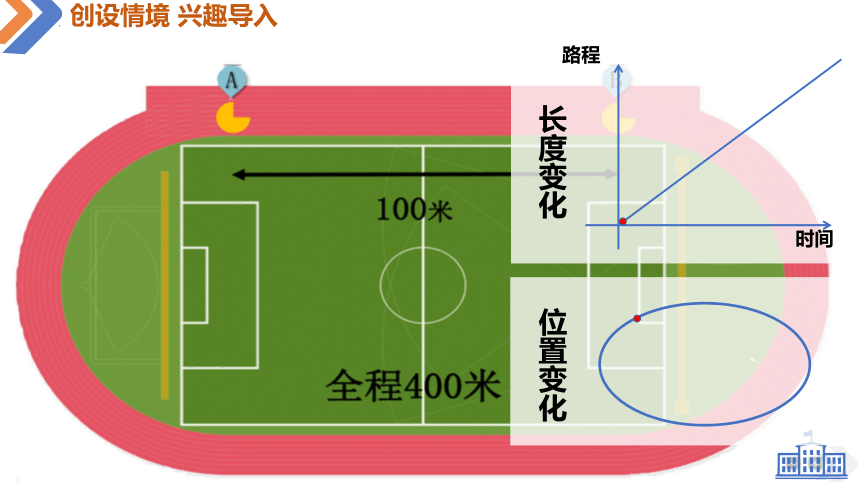
创设情境 兴趣导入
选题的背景
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Donec luctus nibh sit amet sem vulputate venenatis bibendum orci pulvinar.
长度变化
位置变化
时间
路程
观察对比 归纳共性
观察下列各“量”的共同特点:
位移:小船由A地向东南方向航行到达B地
大小:方向:东南方向
速度:小船航行的速度是,速度方向是东南方向
大小:方向:东南方向
重力:物体受到的重力是竖直向下的
物体质量越大,它受到的重力也越大。
大小:方向:竖直向下
浮力:物体在液体中受到的浮力是竖直向上的
物体寝在液体的体积越大,它受到的浮力也越大。
大小:方向:竖直向上
共同特点:“既有大小”、“又有方向”的量
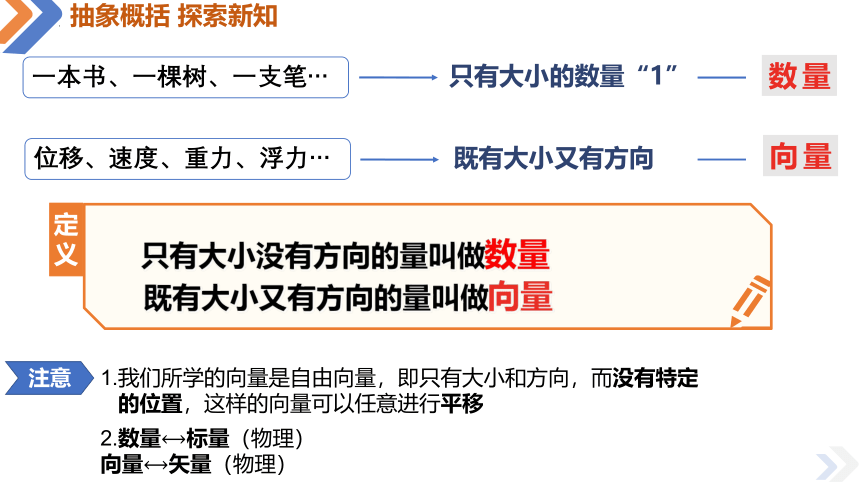
抽象概括 探索新知
选题的背景
一本书、一棵树、一支笔…
只有大小的数量“1”
数量
既有大小又有方向
向量
位移、速度、重力、浮力…
只有大小没有方向的量叫做数量
既有大小又有方向的量叫做向量
定义
注意
1.我们所学的向量是自由向量,即只有大小和方向,而没有特定
的位置,这样的向量可以任意进行平移
2.数量标量(物理)
向量矢量(物理)
数量可由数轴上的点表示,那如何表示一个向量呢?
举例辨析 理解新知
例2.判断下列说法是否正确,并说明理由:
①.由于零上温度可以用正数来表示,零下温度可以用负数来表示,所以温度是向量.
错误,因为温度没有方向。
②.坐标平面上的x轴和y轴是向量.
错误,因为无法刻画x轴和y轴的大小。
例1.举例:根据向量与数量的定义,将学过的 量 进行分类
数量:路程、面积、身高、体重、功、功率……
向量:位移、速度、重力、……
向量的几何表示
02
理解识记 向量表示
数量
向量
用实数表示:如……;
几何表示:
实数
数轴上点
一一对应
以位移为例:
小船以为起点,为终点,我们可以用连接 两点的线段长度代表小船行进的距离,并在终点处加上箭头表示小船行驶的方向.
于是,这条“带有方向的线段”可以表示位移。
受此启发,我们可以用带箭头的线段来表示向量
(终点)
(起点)
在线段的两个端点中,规定一个顺序,
假设是起点,是终点,我们就说线段具有方向(如图)
具有方向的线段叫做有向线段
线段的长度也就是有向线段的大小
理解识记 向量表示
向量的几何表示:
向量常用一条有向线段来表示
有向线段的长度表示向量的大小.
箭头所指的方向表示向量的方向
(终点)
(起点)
向量的符号表示:
向量可以用有向线段的起点和终点字母表示
比如:以点A为起点,点B为终点的向量记作,读作向量AB
在印刷时,常用粗黑体小写字母表示;
手写时,则可用带箭头的小写字母,,来表示.
注意
有向线段三要素:起点、方向、长度
注意
符号表示向量时,起点必须写在终点的前面。
理解识记 相关概念
向量的模:
定义:向量的大小称为向量的长度,或向量的模
表示:在向量符号的两端加上短竖:
如:向量的长度表示成,读作向量的模
特殊向量: ①零向量:模为零的向量叫做零向量,记作
②单位向量:模为1的向量叫做单位向量
注意
1.向量不能比较大小,但向量的模可以比大小;
2.零向量的长度为0,方向不确定,它的方向是任意的;
3.单位向量长度为1,每个单位向量的方向是确定的(由题设规定)
牛刀小试 运用新知
例3:任取不共线的三个点,观察能构成哪些向量?分别用有向线段和字母表示这些向量
B
A
C
例4:如图,分别用向量表示地至、两地的位移,并根据图中的比例尺求出地至、两地的实际距离(精确到)
解: 表示地至地的位移,且
表示地至地的位移, 且
牛刀小试 运用新知
例5:说出下图中各向量的模,并指出其中的单位向量 (小方格边长为1).
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
解: 、、
、 、
、
向量与向量之间有怎样的关系呢?
相等向量与共线向量
03
动脑思考 再探新知
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
观察例5中的向量,它们有什么异同点:
图中的向量、所在的直线平行,方向相同。
向量 ,所在的直线平行,方向相反。
平行向量:
定义:方向相同或相反的非零向量叫做平行向量.
表示:如图,用有向线段表示与是两个平行向量
向量与平行,记作
规定:零向量与任意向量平行,即对于任意向量,都有
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
动脑思考 再探新知
观察例5中的向量,它们有什么异同点:
图中的向量、 平行,方向相同,模相等。
向量 、平行,方向相反,模相等。
相等向量:
定义:长度相等且方向相同的向量叫做相等向量.
长度相等且方向相反的向量叫做相反向量
表示:如图,用有向线段表示与相等,记作
动脑思考 再探新知
如图,是一组平行向量,任作一条与所在直线平行的直线,在上任取一点,则可在上分别做出,,
这就是说,任一组平行向量都可以平移到同一直线上
因此,平行向量也叫做共线向量
任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;同时,两条方向相同且长度相等的有向线段表示同一个向量,因为向量完全由它的模与方向确定。
理解新知 牛刀小试
例6.如图,设是正六边形的中心.
(1)写出图中的共线向量;
(2)分别写出图中与,,相等的向量.
解:(1),,,是共线向量;
,,,是共线向量;
,,,是共线向量.
(2)=
;
.
辨析:①共线向量也就是平行向量,向量“共线”的含义不同于几何中“共线”含义;
② 相等向量一定是共线 (平行) 向量,而共线 (平行) 向量不一定是相等向量
小结与随堂练习
04
典型例题 巩固新知
1.如图所示,是正六边形的中心,且
(1)与的长度相等、方向相反的向量有哪些?
(2)与共线的向量有哪些?
解:(1)与的长度相等、方向相反的向量有,,
(2)与共线的向量有,,,,,,,,
2.判断下列结论是否正确,并说明理由
(1)若与都是单位向量,则。
(2) 方向为南偏西的向量与北偏东的向量是共线向量.
(3)单位向量都相等.
(4)若与是平行向量,则 .
(5)若用有向线段表示的向量与不相等,则点 与不重合
(6)海拔、温度、角度都不是向量
典型例题 巩固新知
3.如图,在矩形中,,,分别为边,的中点,在以、、、、、为起点和终点的所有有向线段表示的向量中,相等的向量共有多少对?
解:长度为1的向量共有18对,其中与同向的有6对,反向的也有6对
与同向的有3对,反向的也有3对
长度为的向量共有4对;
长度为的向量共有2对。
4.已知为平行四边形两条对角线的交点,则的值为( )
...1 .2
C
课时达标检测1(必做)
课本P6《阅读与思考》(选做)
平面向量及其应用
章前语
向量是近代数学中重要和基本概念之一,向量理论具有丰富的物理背景、深刻的数学内涵。向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥着重要作用。
本章我们将通过实际背景引入向量的概念,类比数的运算,学习向量的运算及性质,建立向量的运算体系。在此基础上,用向量的语言、方法表述和解决现实生活、数学和物理中的一些问题。
本章知识结构
平面向量的概念
§6.1
向量的实际背景与概念
向量的几何表示
相等向量与共线向量
小结及随堂练习
向量的实际背景与概念
01
创设情境 兴趣导入
选题的背景
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Donec luctus nibh sit amet sem vulputate venenatis bibendum orci pulvinar.
长度变化
位置变化
时间
路程
观察对比 归纳共性
观察下列各“量”的共同特点:
位移:小船由A地向东南方向航行到达B地
大小:方向:东南方向
速度:小船航行的速度是,速度方向是东南方向
大小:方向:东南方向
重力:物体受到的重力是竖直向下的
物体质量越大,它受到的重力也越大。
大小:方向:竖直向下
浮力:物体在液体中受到的浮力是竖直向上的
物体寝在液体的体积越大,它受到的浮力也越大。
大小:方向:竖直向上
共同特点:“既有大小”、“又有方向”的量
抽象概括 探索新知
选题的背景
一本书、一棵树、一支笔…
只有大小的数量“1”
数量
既有大小又有方向
向量
位移、速度、重力、浮力…
只有大小没有方向的量叫做数量
既有大小又有方向的量叫做向量
定义
注意
1.我们所学的向量是自由向量,即只有大小和方向,而没有特定
的位置,这样的向量可以任意进行平移
2.数量标量(物理)
向量矢量(物理)
数量可由数轴上的点表示,那如何表示一个向量呢?
举例辨析 理解新知
例2.判断下列说法是否正确,并说明理由:
①.由于零上温度可以用正数来表示,零下温度可以用负数来表示,所以温度是向量.
错误,因为温度没有方向。
②.坐标平面上的x轴和y轴是向量.
错误,因为无法刻画x轴和y轴的大小。
例1.举例:根据向量与数量的定义,将学过的 量 进行分类
数量:路程、面积、身高、体重、功、功率……
向量:位移、速度、重力、……
向量的几何表示
02
理解识记 向量表示
数量
向量
用实数表示:如……;
几何表示:
实数
数轴上点
一一对应
以位移为例:
小船以为起点,为终点,我们可以用连接 两点的线段长度代表小船行进的距离,并在终点处加上箭头表示小船行驶的方向.
于是,这条“带有方向的线段”可以表示位移。
受此启发,我们可以用带箭头的线段来表示向量
(终点)
(起点)
在线段的两个端点中,规定一个顺序,
假设是起点,是终点,我们就说线段具有方向(如图)
具有方向的线段叫做有向线段
线段的长度也就是有向线段的大小
理解识记 向量表示
向量的几何表示:
向量常用一条有向线段来表示
有向线段的长度表示向量的大小.
箭头所指的方向表示向量的方向
(终点)
(起点)
向量的符号表示:
向量可以用有向线段的起点和终点字母表示
比如:以点A为起点,点B为终点的向量记作,读作向量AB
在印刷时,常用粗黑体小写字母表示;
手写时,则可用带箭头的小写字母,,来表示.
注意
有向线段三要素:起点、方向、长度
注意
符号表示向量时,起点必须写在终点的前面。
理解识记 相关概念
向量的模:
定义:向量的大小称为向量的长度,或向量的模
表示:在向量符号的两端加上短竖:
如:向量的长度表示成,读作向量的模
特殊向量: ①零向量:模为零的向量叫做零向量,记作
②单位向量:模为1的向量叫做单位向量
注意
1.向量不能比较大小,但向量的模可以比大小;
2.零向量的长度为0,方向不确定,它的方向是任意的;
3.单位向量长度为1,每个单位向量的方向是确定的(由题设规定)
牛刀小试 运用新知
例3:任取不共线的三个点,观察能构成哪些向量?分别用有向线段和字母表示这些向量
B
A
C
例4:如图,分别用向量表示地至、两地的位移,并根据图中的比例尺求出地至、两地的实际距离(精确到)
解: 表示地至地的位移,且
表示地至地的位移, 且
牛刀小试 运用新知
例5:说出下图中各向量的模,并指出其中的单位向量 (小方格边长为1).
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
解: 、、
、 、
、
向量与向量之间有怎样的关系呢?
相等向量与共线向量
03
动脑思考 再探新知
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
观察例5中的向量,它们有什么异同点:
图中的向量、所在的直线平行,方向相同。
向量 ,所在的直线平行,方向相反。
平行向量:
定义:方向相同或相反的非零向量叫做平行向量.
表示:如图,用有向线段表示与是两个平行向量
向量与平行,记作
规定:零向量与任意向量平行,即对于任意向量,都有
A
B
C
D
E
F
H
G
M
N
Q
P
L
Z
K
T
动脑思考 再探新知
观察例5中的向量,它们有什么异同点:
图中的向量、 平行,方向相同,模相等。
向量 、平行,方向相反,模相等。
相等向量:
定义:长度相等且方向相同的向量叫做相等向量.
长度相等且方向相反的向量叫做相反向量
表示:如图,用有向线段表示与相等,记作
动脑思考 再探新知
如图,是一组平行向量,任作一条与所在直线平行的直线,在上任取一点,则可在上分别做出,,
这就是说,任一组平行向量都可以平移到同一直线上
因此,平行向量也叫做共线向量
任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;同时,两条方向相同且长度相等的有向线段表示同一个向量,因为向量完全由它的模与方向确定。
理解新知 牛刀小试
例6.如图,设是正六边形的中心.
(1)写出图中的共线向量;
(2)分别写出图中与,,相等的向量.
解:(1),,,是共线向量;
,,,是共线向量;
,,,是共线向量.
(2)=
;
.
辨析:①共线向量也就是平行向量,向量“共线”的含义不同于几何中“共线”含义;
② 相等向量一定是共线 (平行) 向量,而共线 (平行) 向量不一定是相等向量
小结与随堂练习
04
典型例题 巩固新知
1.如图所示,是正六边形的中心,且
(1)与的长度相等、方向相反的向量有哪些?
(2)与共线的向量有哪些?
解:(1)与的长度相等、方向相反的向量有,,
(2)与共线的向量有,,,,,,,,
2.判断下列结论是否正确,并说明理由
(1)若与都是单位向量,则。
(2) 方向为南偏西的向量与北偏东的向量是共线向量.
(3)单位向量都相等.
(4)若与是平行向量,则 .
(5)若用有向线段表示的向量与不相等,则点 与不重合
(6)海拔、温度、角度都不是向量
典型例题 巩固新知
3.如图,在矩形中,,,分别为边,的中点,在以、、、、、为起点和终点的所有有向线段表示的向量中,相等的向量共有多少对?
解:长度为1的向量共有18对,其中与同向的有6对,反向的也有6对
与同向的有3对,反向的也有3对
长度为的向量共有4对;
长度为的向量共有2对。
4.已知为平行四边形两条对角线的交点,则的值为( )
...1 .2
C
课时达标检测1(必做)
课本P6《阅读与思考》(选做)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
