17.1勾股定理(1) 课件(26张PPT)
文档属性
| 名称 | 17.1勾股定理(1) 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 19:15:05 | ||
图片预览






文档简介
(共26张PPT)
17.1勾股定理(1)
人教版八年级下册
教学目标
1. 了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.
2. 能用勾股定理解决一些简单问题.
3. 通过用多种方法证明勾股定理,培养学生发散思维能力.
温故知新
1、任意三角形三边满足怎样的关系?
2、对于等腰三角形,三边之间存在怎样的特殊关系?等边三角形呢?
3、对于直角三角形,三边之间存在怎样的特殊关系?
新知讲解
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
知识点 1
勾股定理的发现及证明
新知讲解
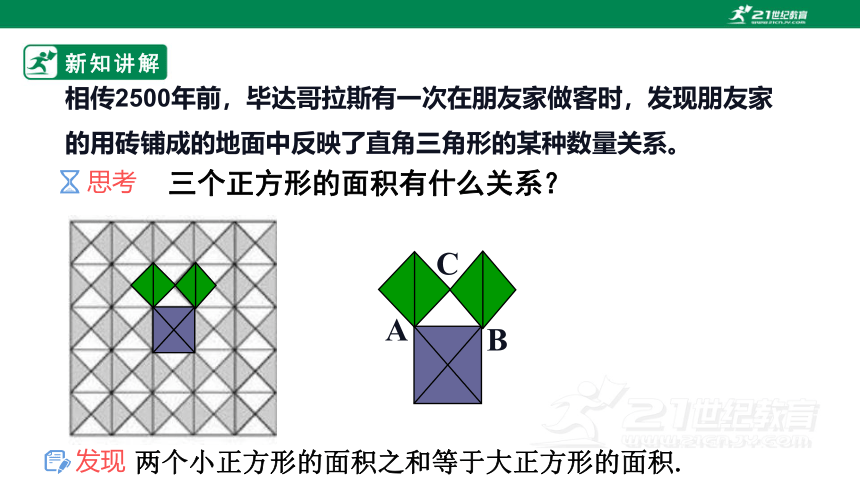
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系。
C
B
A
思考
三个正方形的面积有什么关系?
发现
两个小正方形的面积之和等于大正方形的面积.
新知讲解
思考
等腰直角三角形三条边长度之间有怎样的特殊关系?
S
S1
S2
小结
等腰直角三角形斜边的平方等于两直角边的平方和.
S=S1+S2,
即c2=a2+b2.
a b
c
新知讲解
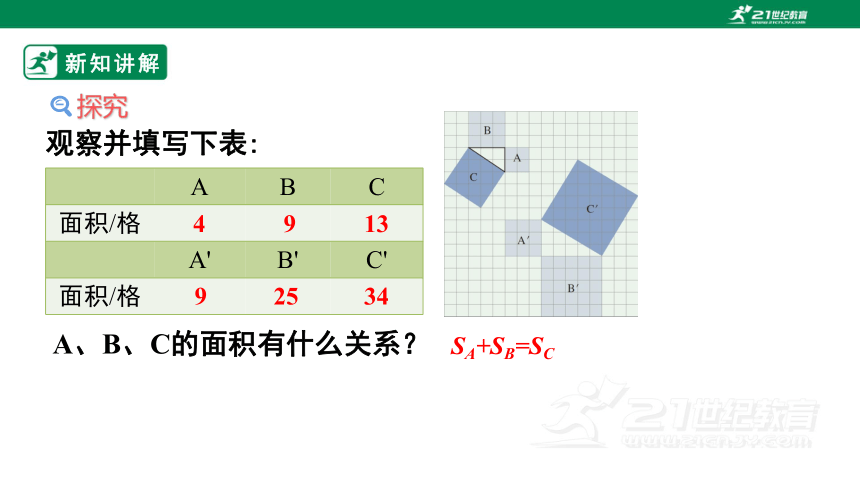
观察并填写下表:
A B C
面积/格
A' B' C'
面积/格
A、B、C的面积有什么关系?
SA+SB=SC
9
25
34
4
9
13
探究
新知讲解
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
提问
规律
a
b
c
是不是所有的直角三角形都具有这样的结论呢?
新知讲解
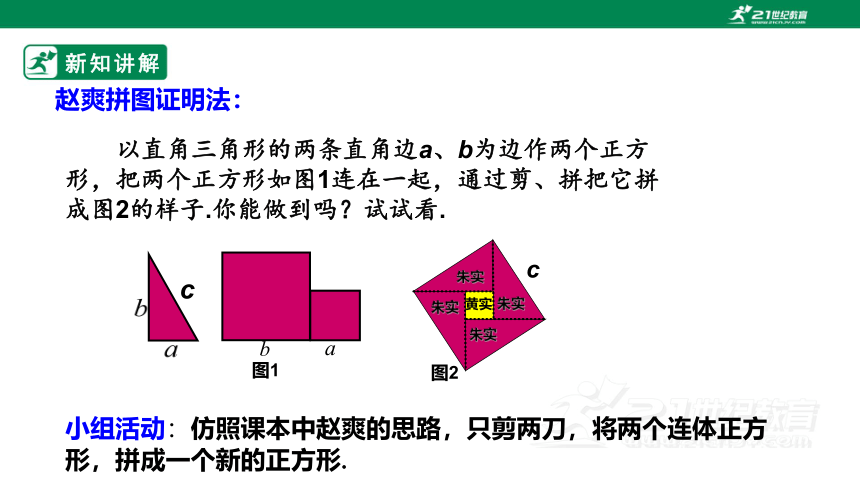
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
赵爽拼图证明法:
c
图1
黄实
朱实
朱实
朱实
朱实
图2
c
小组活动:仿照课本中赵爽的思路,只剪两刀,将两个连体正方
形,拼成一个新的正方形.
新知讲解
“赵爽弦图”
黄实
朱实
朱实
朱实
朱实
c
a
b
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
证明:
新知讲解
毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
新知讲解
a
a
b
b
c
c
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
证明:
∵
,
,
新知讲解
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
a
b
c
符号语言:Rt△ABC中,∠C=90°,
则 .
A
B
C
巩固练习
1.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:根据图形正方形E 的边长为:
故E的面积为:252=625.
教材同步练习
巩固练习
2.作 8 个全等的直角三角形(2 条直角边长分别为 a、b斜边长为 c)再作3个边长分别为 a、b、c 的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗 写出你的验证过程.
解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4× ab,
由右图可得(a+b)2=c2+4× ab.
所以a2+b2=c2.
新知讲解
知识点 2
勾股定理的变形
A
B
C
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方.
c
b
a
a2 + b2 =c2
a2=c2-b2
b2 =c2-a2
例题讲解
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
例1 在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
提示:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
(舍去)
(舍去)
变式练习
3.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
b=8
c=13
a=20
教材同步练习
新知讲解
例2
变式练习
4、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
拓展提高
1. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,
那么正方形ABCD的面积为( )
A. B.3
C. D.5
B
E
拓展提高
2、在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
提示:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
拓展提高
3、已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
提示:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
17.1勾股定理(1)
人教版八年级下册
教学目标
1. 了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.
2. 能用勾股定理解决一些简单问题.
3. 通过用多种方法证明勾股定理,培养学生发散思维能力.
温故知新
1、任意三角形三边满足怎样的关系?
2、对于等腰三角形,三边之间存在怎样的特殊关系?等边三角形呢?
3、对于直角三角形,三边之间存在怎样的特殊关系?
新知讲解
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
知识点 1
勾股定理的发现及证明
新知讲解
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系。
C
B
A
思考
三个正方形的面积有什么关系?
发现
两个小正方形的面积之和等于大正方形的面积.
新知讲解
思考
等腰直角三角形三条边长度之间有怎样的特殊关系?
S
S1
S2
小结
等腰直角三角形斜边的平方等于两直角边的平方和.
S=S1+S2,
即c2=a2+b2.
a b
c
新知讲解
观察并填写下表:
A B C
面积/格
A' B' C'
面积/格
A、B、C的面积有什么关系?
SA+SB=SC
9
25
34
4
9
13
探究
新知讲解
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过前面的探究活动,你发现了直角三角形三边之间的关系规律了吗?
提问
规律
a
b
c
是不是所有的直角三角形都具有这样的结论呢?
新知讲解
以直角三角形的两条直角边a、b为边作两个正方形,把两个正方形如图1连在一起,通过剪、拼把它拼成图2的样子.你能做到吗?试试看.
赵爽拼图证明法:
c
图1
黄实
朱实
朱实
朱实
朱实
图2
c
小组活动:仿照课本中赵爽的思路,只剪两刀,将两个连体正方
形,拼成一个新的正方形.
新知讲解
“赵爽弦图”
黄实
朱实
朱实
朱实
朱实
c
a
b
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
证明:
新知讲解
毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图示进行拼图,然后分析其面积关系后证明吧.
a
a
a
a
b
b
b
b
c
c
c
c
∴a2+b2+2ab=c2+2ab,
∴a2 +b2 =c2.
证明:∵S大正方形=(a+b)2=a2+b2+2ab,
S大正方形=4S直角三角形+ S小正方形
=4× ab+c2
=c2+2ab,
新知讲解
a
a
b
b
c
c
∴a2 + b2 = c2.
美国第二十任总统伽菲尔德的“总统证法”.
如图,图中的三个三角形都是直角三角形,求证:a2 + b2 = c2.
证明:
∵
,
,
新知讲解
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
即直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
a
b
c
符号语言:Rt△ABC中,∠C=90°,
则 .
A
B
C
巩固练习
1.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.
解:根据图形正方形E 的边长为:
故E的面积为:252=625.
教材同步练习
巩固练习
2.作 8 个全等的直角三角形(2 条直角边长分别为 a、b斜边长为 c)再作3个边长分别为 a、b、c 的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗 写出你的验证过程.
解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4× ab,
由右图可得(a+b)2=c2+4× ab.
所以a2+b2=c2.
新知讲解
知识点 2
勾股定理的变形
A
B
C
勾股定理给出了直角三角形三边之间的关系,即两直角边的平方和等于斜边的平方.
c
b
a
a2 + b2 =c2
a2=c2-b2
b2 =c2-a2
例题讲解
(1)若a:b=1:2 ,c=5,求a;
(2)若b=15,∠A=30°,求a,c.
例1 在Rt△ABC中, ∠C=90°.
解:
(1)设a=x,b=2x,根据勾股定理建立方程得
x2+(2x)2=52,
解得
(2)
因此设a=x,c=2x,根据勾股定理建立方程得
(2x)2-x2=152,
解得
提示:已知直角三角形两边关系和第三边的长求未知两边时,要运用方程思想设未知数,根据勾股定理列方程求解.
(舍去)
(舍去)
变式练习
3.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
b=8
c=13
a=20
教材同步练习
新知讲解
例2
变式练习
4、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
课堂小结
勾股定理
内容
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意
在直角三角形中
看清哪个角是直角
已知两边没有指明是直角边还是斜边时一定要分类讨论
证明
拓展提高
1. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,
那么正方形ABCD的面积为( )
A. B.3
C. D.5
B
E
拓展提高
2、在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
提示:当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易丢解.
拓展提高
3、已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
提示:由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
