6.1.3 平方根 教学课件(共20张PPT)
文档属性
| 名称 | 6.1.3 平方根 教学课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 21:52:27 | ||
图片预览








文档简介
(共20张PPT)
第六章 实数
6.1 平方根
第3课时 平方根
学习目标
1.理解平方根的概念,明确平方根与算术平方根之间的联系与区别.
2.能用符号正确地表示一个数的平方根,理解开方运算和平方运算之间的互逆关系.会求一个非负数的平方根.
重点:平方根的概念和求一个非负数的平方根.
难点:理解并运用 的双重非负性.
课前预习
阅读课本第P44-46页内容,学习本节主要内容.
平方根
两
开平方
二次方根
互为相反数
没有平方根
0
新课导入
什么数的平方是49?平方得81的数有几个?分别是什么?
一对互为相反数的平方有什么关系?
7是前面学习过的49的算术平方根,
-7与49的算术平方根有什么关系?
1. 如果一个数的平方等于 9,这个数是多少?
∵32 = 9,(-3)2 = 9
2. 完成左侧
表格:
1
3
4
6
思考:一对互为相反数的两个数的平方,结果是什么关系?你从中得出什么结论?
∴这个数是 3 或 -3.
探究新知
平方根的概念、开平方
(1)一般地,如果一个数的平方等于 a,那么这个数叫做
a 的平方根或二次方根.
●这就是说 x2 = a,那么 x 叫做 a 的平方根.
(2)求一个数 a 的平方根的运算,叫做开平方.
知识归纳
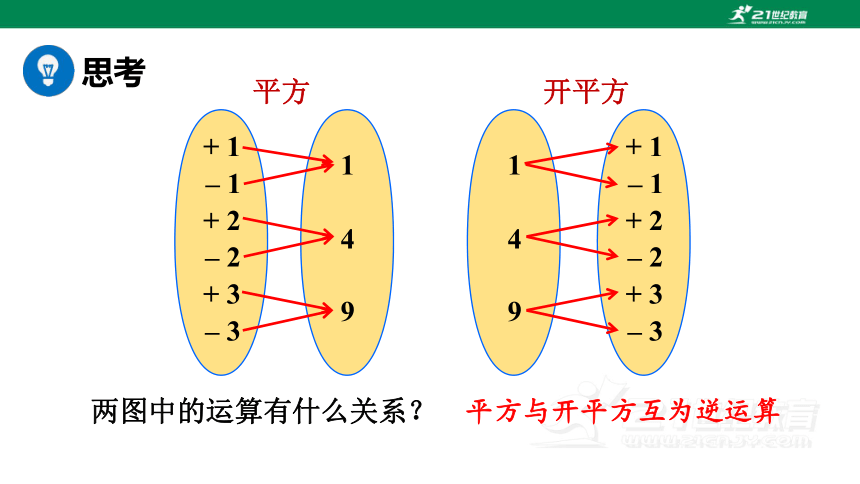
思考
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
平方
开平方
两图中的运算有什么关系?
平方与开平方互为逆运算
(1) 1. 144的平方根是什么?
(2) 的平方根是什么?
(3) 0的平方根是什么?
(4) -4有没有平方根?为什么?
没有,因为一个数的平方不可能是负数.
±12
±
0
课堂练习
思考
正数有几个平方根?
0有几个平方根?
负数有平方根吗?为什么?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为 02 = 0,并且任何一个不为 0 的数的平方都不等于 0,所以 0 的平方根是 0.
在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
平方根的性质
(1) 正数有两个平方根,它们互为相反数;
(2) 0 的平方根是 0;
(3) 负数没有平方根.
知识归纳
例1 求下列各式的值:
(1) ; (2) ; (3) .
解:(1) = 6 ;
(2) = -0.9 ;
(3) = ± ;
例题分析
例2 一个正数的两个平方根分别是2a+1和a-4,求这个数.
解:由于一个正数的两个平方根是 2a+1 和 a-4,
则有 2a+1+a-4=0,
即 3a-3=0,
解得 a=1.
所以这个数为 (2a+1)2=(2+1)2=9.
一个正数有两个平方根,它们互为相反数.
提示
例3 求下列各式中 x 的值:
(1) x2=361; (2) 81x2-49=0;
(3) 49(x2+1)=50; (4) (3x-1)2=(-5)2.
解:(1)∵x2=361,
∴开平方得x=± =±19;
(2)整理81x2-49=0,得x2= ,
∴开平方得x=± =± ;
解:(3)整理49(x2+1)=50,得x2= ,
∴开平方得x=± =± ;
(4)∵(3x-1)=(-5)2,∴开平方得3x-1=±5,
当3x-1=5时,x=2,
当3x-1=-5时,x=- ,
综上所述,x=2或- .
1.求下列各数的平方根:
(1)49 ;(2) ;(3) ;(4)0.0016 .
解:(1)±7;
(2)± ;
(3)± ;
(4)±0.04 .
课堂练习
2.判断下列说法是否正确:
(1) 5是25的算术平方根;
(2) 是 的一个平方根;
(3) (-4)2的平方根是-4;
(4) 0的平方根与算术平方根都是0.
解:(1) (2) (4)正确,(3)错误,因为(-4)2的平方根是±4.
D
2
4
16
3.下列计算正确的是( )
A. =±5 B.± =3
C. =±3 D.± =±4
4.(1)若 x 的平方根是±2,则 =_____;
(2)若 =2,则 x=_____;
(3)若 的平方根是±2,则 x=_____.
解:∵2a-1的平方根为± ,
∴2a-1=3,∴a=2.
∵3a-2b+1的平方根为±3,
∴3×2-2b+1=9,∴b=-1,
∴4a-b=9,
∴4a-b的平方根为±3.
5.2a-1的平方根为± ,3a-2b+1的平方根为±3,求4a-b的平方根.
平方根
平方根的概念、开平方
平方根的性质
运用平方根的概念和性质解决问题
课堂小结
1.教材P47~48习题6.1第3,4,8,11题;
2.完成对应课时练习.
作业布置
第六章 实数
6.1 平方根
第3课时 平方根
学习目标
1.理解平方根的概念,明确平方根与算术平方根之间的联系与区别.
2.能用符号正确地表示一个数的平方根,理解开方运算和平方运算之间的互逆关系.会求一个非负数的平方根.
重点:平方根的概念和求一个非负数的平方根.
难点:理解并运用 的双重非负性.
课前预习
阅读课本第P44-46页内容,学习本节主要内容.
平方根
两
开平方
二次方根
互为相反数
没有平方根
0
新课导入
什么数的平方是49?平方得81的数有几个?分别是什么?
一对互为相反数的平方有什么关系?
7是前面学习过的49的算术平方根,
-7与49的算术平方根有什么关系?
1. 如果一个数的平方等于 9,这个数是多少?
∵32 = 9,(-3)2 = 9
2. 完成左侧
表格:
1
3
4
6
思考:一对互为相反数的两个数的平方,结果是什么关系?你从中得出什么结论?
∴这个数是 3 或 -3.
探究新知
平方根的概念、开平方
(1)一般地,如果一个数的平方等于 a,那么这个数叫做
a 的平方根或二次方根.
●这就是说 x2 = a,那么 x 叫做 a 的平方根.
(2)求一个数 a 的平方根的运算,叫做开平方.
知识归纳
思考
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
平方
开平方
两图中的运算有什么关系?
平方与开平方互为逆运算
(1) 1. 144的平方根是什么?
(2) 的平方根是什么?
(3) 0的平方根是什么?
(4) -4有没有平方根?为什么?
没有,因为一个数的平方不可能是负数.
±12
±
0
课堂练习
思考
正数有几个平方根?
0有几个平方根?
负数有平方根吗?为什么?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为 02 = 0,并且任何一个不为 0 的数的平方都不等于 0,所以 0 的平方根是 0.
在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
平方根的性质
(1) 正数有两个平方根,它们互为相反数;
(2) 0 的平方根是 0;
(3) 负数没有平方根.
知识归纳
例1 求下列各式的值:
(1) ; (2) ; (3) .
解:(1) = 6 ;
(2) = -0.9 ;
(3) = ± ;
例题分析
例2 一个正数的两个平方根分别是2a+1和a-4,求这个数.
解:由于一个正数的两个平方根是 2a+1 和 a-4,
则有 2a+1+a-4=0,
即 3a-3=0,
解得 a=1.
所以这个数为 (2a+1)2=(2+1)2=9.
一个正数有两个平方根,它们互为相反数.
提示
例3 求下列各式中 x 的值:
(1) x2=361; (2) 81x2-49=0;
(3) 49(x2+1)=50; (4) (3x-1)2=(-5)2.
解:(1)∵x2=361,
∴开平方得x=± =±19;
(2)整理81x2-49=0,得x2= ,
∴开平方得x=± =± ;
解:(3)整理49(x2+1)=50,得x2= ,
∴开平方得x=± =± ;
(4)∵(3x-1)=(-5)2,∴开平方得3x-1=±5,
当3x-1=5时,x=2,
当3x-1=-5时,x=- ,
综上所述,x=2或- .
1.求下列各数的平方根:
(1)49 ;(2) ;(3) ;(4)0.0016 .
解:(1)±7;
(2)± ;
(3)± ;
(4)±0.04 .
课堂练习
2.判断下列说法是否正确:
(1) 5是25的算术平方根;
(2) 是 的一个平方根;
(3) (-4)2的平方根是-4;
(4) 0的平方根与算术平方根都是0.
解:(1) (2) (4)正确,(3)错误,因为(-4)2的平方根是±4.
D
2
4
16
3.下列计算正确的是( )
A. =±5 B.± =3
C. =±3 D.± =±4
4.(1)若 x 的平方根是±2,则 =_____;
(2)若 =2,则 x=_____;
(3)若 的平方根是±2,则 x=_____.
解:∵2a-1的平方根为± ,
∴2a-1=3,∴a=2.
∵3a-2b+1的平方根为±3,
∴3×2-2b+1=9,∴b=-1,
∴4a-b=9,
∴4a-b的平方根为±3.
5.2a-1的平方根为± ,3a-2b+1的平方根为±3,求4a-b的平方根.
平方根
平方根的概念、开平方
平方根的性质
运用平方根的概念和性质解决问题
课堂小结
1.教材P47~48习题6.1第3,4,8,11题;
2.完成对应课时练习.
作业布置
