第二节《直角三角形》能力测试(附答案)
文档属性
| 名称 | 第二节《直角三角形》能力测试(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 257.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-25 23:22:48 | ||
图片预览


文档简介
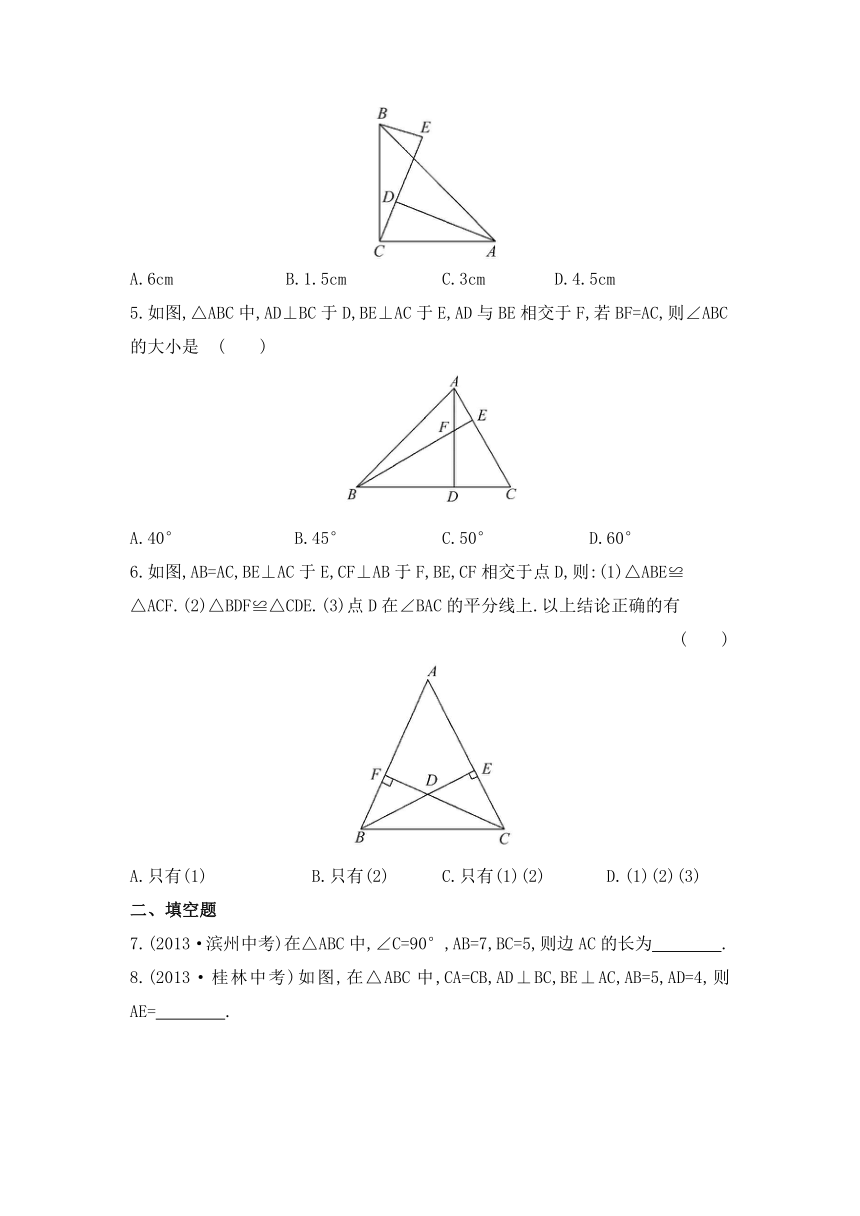
北师版数学第一章《三角形的证明》
第二节《直角三角形》能力测试
一、选择题
1.(2013·济南中考)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆的高度(滑轮上方的部分忽略不计)为 ( )
A.12m B.13 m C.16 m D.17 m
2.下列命题的逆命题不正确的是 ( )
A.线段垂直平分线上的点到线段两个端点的距离相等
B.两直线平行,内错角相等
C.等腰三角形的两个底角相等
D.对顶角相等
3.如图,小明在广场上先向东走10m,又向南走40m,再向西走20m,又向南走40m,再向东走70m.则小明到达的终止点与出发点的距离是 ( )
A.90m B.100m C.120m D.150m
4.如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是 ( )
A.6cm B.1.5cm C.3cm D.4.5cm
5.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是 ( )
A.40° B.45° C.50° D.60°
6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF相交于点D,则:(1)△ABE≌
△ACF.(2)△BDF≌△CDE.(3)点D在∠BAC的平分线上.以上结论正确的有
( )
A.只有(1) B.只有(2) C.只有(1)(2) D.(1)(2)(3)
二、填空题
7.(2013·滨州中考)在△ABC中,∠C=90°,AB=7,BC=5,则边AC的长为 .
8.(2013·桂林中考)如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE= .
9.图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长是 .
10.如图,AB⊥AC,DC⊥AC,AD=BC,则AD和BC的位置关系是 .
11.如图所示,AB=CD,AE⊥BD于E,CF⊥BD于F,AE=CF,则图中全等三角形有
对.
12.如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
三、解答题(共26分)
13.(8分)如图所示,在△ABC中,AB=13,BC=14,AC=15,求BC边上的高线AD的长.
14.(8分)已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3.求:四边形ABCD的面积.
15.(12分)如图,已知∠ABC=∠ADC=90°,E是AC上一点,AB=AD,求证:EB=ED.
【拓展延伸】
16.(10分)阅读下面的情景对话,然后解答问题:
(1)根据“奇异三角形”的定义,请你判断小华提出的命题“等边三角形一定是奇异三角形”是真命题还是假命题.
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c.
17.(14分)如图,等腰直角三角形ACB,∠ACB=90°,CA=CB.
操作:如图1,过点A任作一条直线(不经过点C和点B)交BC所在直线于点D,过点B作BF⊥AD交AD于点F,交AC所在直线于点E,连接DE.
(1)猜想△CDE的形状(直接写出猜想,不需证明).
(2)请你利用图2,图3作与上述位置不同的直线,然后按上述方法操作.画出相应的图形.
(3)在经历(2)之后,若你认为(1)中的结论是成立的,请你利用图2加以证明;若你认为不成立,请你利用其中一图说明理由.
答案解析
1. D.2. D. 3. B.4. C.5. B.6. D.
7. 2 8. 3 9. 76 10.平行 11. 3 12. 5cm或10cm
13.在Rt△ABD和Rt△ACD中,关系式有AD2+BD2=AB2,AD2+CD2=AC2.
因为AD是Rt△ABD和Rt△ACD的公共边,所以可以得AD2=AB2-BD2,
AD2=AC2-CD2.AB2-BD2=AC2-CD2.
设BD=x,则CD=14-x,可得方程132-x2=152-(14-x)2,解方程得x=5,再由勾股定理得AD=12.
14.作DE∥AB,连接BD,
∴∠ABD=∠EDB,同理,∠ADB=∠EBD,又因BD=DB,∴△ABD≌△EDB,
∴DE=AB=4,BE=AD=3.∵BC=6,∴EC=EB=3.
∵DE2+CE2=32+42=25=CD2,∴△DEC为直角三角形.又∵EC=EB=3,∴△DBC为等腰三角形,DB=DC=5.在△BDA中AD2+AB2=32+42=25=BD2,∴△BDA是直角三角形.它们的面积分别为S△BDA=×3×4=6;S△DBC=×6×4=12.∴S四边形ABCD=S△BDA+S△DBC=6+12=18.
15.在Rt△ADC和Rt△ABC中,∴Rt△ABC≌Rt△ADC(HL),∴∠DCE=∠BCE,DC=BC,∴在△DCE和△BCE中,∴△DCE≌△BCE(SAS),∴EB=ED.
【拓展延伸】
16. (1)设等边三角形的边长为a,则a2+a2=2a2,∴符合“奇异三角形”的定义.∴小华提出的命题是真命题.
(2)∵∠C=90°,则a2+b2=c2 ①,∵Rt△ABC是奇异三角形,且b>a,∴a2+c2=2b2 ②,由①②得:b=a,c=a,∴a∶b∶c=1∶∶.
17.(1)△CDE是等腰直角三角形.(2)据要求画出图形如下:
(3)结论成立.
证明:∵∠ACB=90°,AF⊥BE,
∴∠ADC+∠CBE=90°,∠CBE+∠CEB=90°,∴∠ADC=∠CEB.
∵在Rt△ACD和Rt△BCE中,CA=CB,∠ADC=∠CEB,∠ACD=∠BCE=90°,
∴△ACD≌△BCE.∴CD=CE,∴△CDE是等腰直角三角形.
第二节《直角三角形》能力测试
一、选择题
1.(2013·济南中考)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆的高度(滑轮上方的部分忽略不计)为 ( )
A.12m B.13 m C.16 m D.17 m
2.下列命题的逆命题不正确的是 ( )
A.线段垂直平分线上的点到线段两个端点的距离相等
B.两直线平行,内错角相等
C.等腰三角形的两个底角相等
D.对顶角相等
3.如图,小明在广场上先向东走10m,又向南走40m,再向西走20m,又向南走40m,再向东走70m.则小明到达的终止点与出发点的距离是 ( )
A.90m B.100m C.120m D.150m
4.如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.DE=6cm,AD=9cm,则BE的长是 ( )
A.6cm B.1.5cm C.3cm D.4.5cm
5.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是 ( )
A.40° B.45° C.50° D.60°
6.如图,AB=AC,BE⊥AC于E,CF⊥AB于F,BE,CF相交于点D,则:(1)△ABE≌
△ACF.(2)△BDF≌△CDE.(3)点D在∠BAC的平分线上.以上结论正确的有
( )
A.只有(1) B.只有(2) C.只有(1)(2) D.(1)(2)(3)
二、填空题
7.(2013·滨州中考)在△ABC中,∠C=90°,AB=7,BC=5,则边AC的长为 .
8.(2013·桂林中考)如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE= .
9.图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图乙所示的“数学风车”,则这个风车的外围周长是 .
10.如图,AB⊥AC,DC⊥AC,AD=BC,则AD和BC的位置关系是 .
11.如图所示,AB=CD,AE⊥BD于E,CF⊥BD于F,AE=CF,则图中全等三角形有
对.
12.如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P,Q两点分别在AC和AC的垂线AX上移动,则当AP= 时,才能使△ABC和△APQ全等.
三、解答题(共26分)
13.(8分)如图所示,在△ABC中,AB=13,BC=14,AC=15,求BC边上的高线AD的长.
14.(8分)已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3.求:四边形ABCD的面积.
15.(12分)如图,已知∠ABC=∠ADC=90°,E是AC上一点,AB=AD,求证:EB=ED.
【拓展延伸】
16.(10分)阅读下面的情景对话,然后解答问题:
(1)根据“奇异三角形”的定义,请你判断小华提出的命题“等边三角形一定是奇异三角形”是真命题还是假命题.
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c.
17.(14分)如图,等腰直角三角形ACB,∠ACB=90°,CA=CB.
操作:如图1,过点A任作一条直线(不经过点C和点B)交BC所在直线于点D,过点B作BF⊥AD交AD于点F,交AC所在直线于点E,连接DE.
(1)猜想△CDE的形状(直接写出猜想,不需证明).
(2)请你利用图2,图3作与上述位置不同的直线,然后按上述方法操作.画出相应的图形.
(3)在经历(2)之后,若你认为(1)中的结论是成立的,请你利用图2加以证明;若你认为不成立,请你利用其中一图说明理由.
答案解析
1. D.2. D. 3. B.4. C.5. B.6. D.
7. 2 8. 3 9. 76 10.平行 11. 3 12. 5cm或10cm
13.在Rt△ABD和Rt△ACD中,关系式有AD2+BD2=AB2,AD2+CD2=AC2.
因为AD是Rt△ABD和Rt△ACD的公共边,所以可以得AD2=AB2-BD2,
AD2=AC2-CD2.AB2-BD2=AC2-CD2.
设BD=x,则CD=14-x,可得方程132-x2=152-(14-x)2,解方程得x=5,再由勾股定理得AD=12.
14.作DE∥AB,连接BD,
∴∠ABD=∠EDB,同理,∠ADB=∠EBD,又因BD=DB,∴△ABD≌△EDB,
∴DE=AB=4,BE=AD=3.∵BC=6,∴EC=EB=3.
∵DE2+CE2=32+42=25=CD2,∴△DEC为直角三角形.又∵EC=EB=3,∴△DBC为等腰三角形,DB=DC=5.在△BDA中AD2+AB2=32+42=25=BD2,∴△BDA是直角三角形.它们的面积分别为S△BDA=×3×4=6;S△DBC=×6×4=12.∴S四边形ABCD=S△BDA+S△DBC=6+12=18.
15.在Rt△ADC和Rt△ABC中,∴Rt△ABC≌Rt△ADC(HL),∴∠DCE=∠BCE,DC=BC,∴在△DCE和△BCE中,∴△DCE≌△BCE(SAS),∴EB=ED.
【拓展延伸】
16. (1)设等边三角形的边长为a,则a2+a2=2a2,∴符合“奇异三角形”的定义.∴小华提出的命题是真命题.
(2)∵∠C=90°,则a2+b2=c2 ①,∵Rt△ABC是奇异三角形,且b>a,∴a2+c2=2b2 ②,由①②得:b=a,c=a,∴a∶b∶c=1∶∶.
17.(1)△CDE是等腰直角三角形.(2)据要求画出图形如下:
(3)结论成立.
证明:∵∠ACB=90°,AF⊥BE,
∴∠ADC+∠CBE=90°,∠CBE+∠CEB=90°,∴∠ADC=∠CEB.
∵在Rt△ACD和Rt△BCE中,CA=CB,∠ADC=∠CEB,∠ACD=∠BCE=90°,
∴△ACD≌△BCE.∴CD=CE,∴△CDE是等腰直角三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
