四则混合运算(2)课件(共20张PPT)西师大版四年级下册数学
文档属性
| 名称 | 四则混合运算(2)课件(共20张PPT)西师大版四年级下册数学 |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-14 14:51:47 | ||
图片预览







文档简介
(共20张PPT)
四则混合运算(2)
复习导入
3.在四则混合运算中,只有加减法或只有乘除法,运算顺序是( )。
2.算式中带有括号的,应先算( ),再算( )。
1.在四则混合运算中,既有加减法又有乘除法,运算顺序是( )。
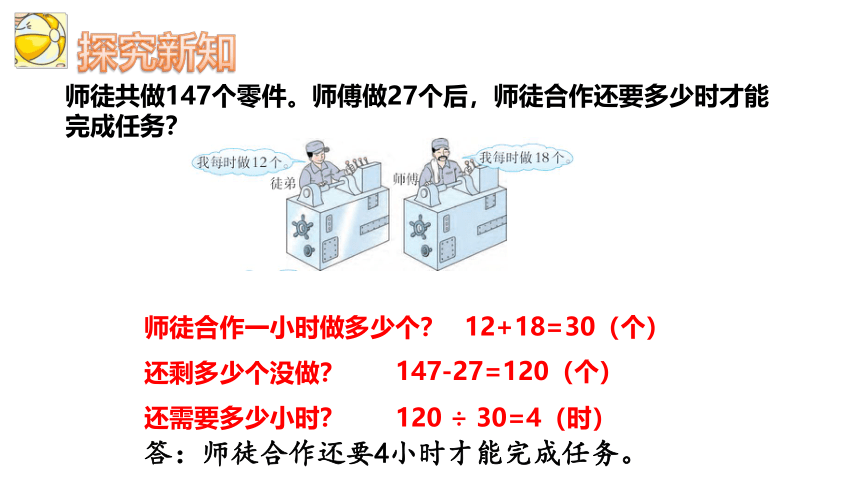
探究新知
师徒合作一小时做多少个?
还剩多少个没做?
还需要多少小时?
12+18=30(个)
147-27=120(个)
120 ÷ 30=4(时)
答:师徒合作还要4小时才能完成任务。
师徒共做147个零件。师傅做27个后,师徒合作还要多少时才能完成任务?
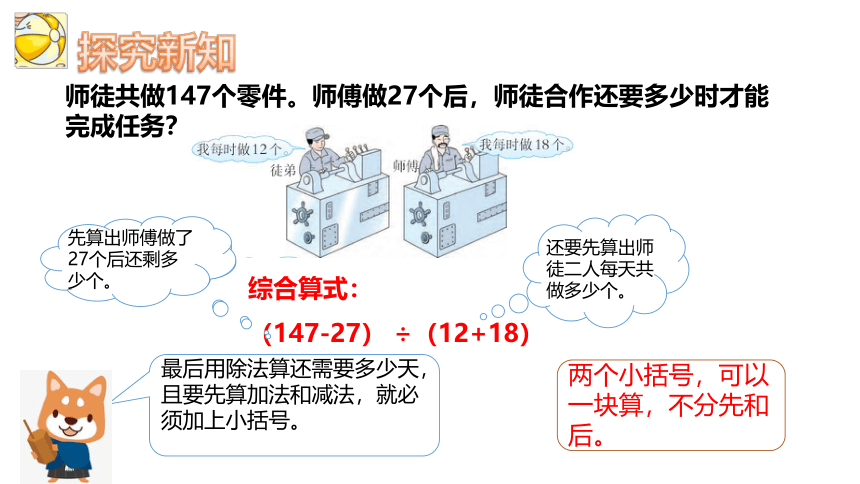
探究新知
综合算式:
(147-27) ÷(12+18)
师徒共做147个零件。师傅做27个后,师徒合作还要多少时才能完成任务?
算式中为什么要加两个小括号?
先算出师傅做了27个后还剩多少个。
还要先算出师徒二人每天共做多少个。
两个小括号,可以一块算,不分先和后。
最后用除法算还需要多少天,且要先算加法和减法,就必须加上小括号。
探究新知
1.说一说运算顺序,并计算。
(32+48)×(12 × 14)
(32+48)×(12 × 14)
=80 ×168
=13440
①
②
①
先算两个小括号里的加法和乘法,最后算括号外面的乘法。
探究新知
1.说一说运算顺序,并计算。
630 ÷ (15+15 × 5)
630 ÷ (15+15 × 5)
=630 ÷(15+75)
=630 ÷90
=7
①
②
先算小括号里的乘法和加法,最后算括号外面的除法。
③
探究新知
1.说一说运算顺序,并计算。
225-45 ×4
=225-180
=45
(225-45)×4
=180 ×4
=720
①
②
①
②
没有括号时,要先算乘法再算减法,当减法上加了小括号,就要先算减法再算乘法。运算顺序不同,计算的结果也不同。
254-250=4
22+29=51
4×51=
要想先算减法和加法,必须要加上小括号。
(254-250)×(22+29)
=4 × 51
=204
把下面的算式改写成一个综合算式。
探究新知
“[]”叫中括号。计算时要先算小括号里面的,再算中括号里面的。
450÷[(17+8)×3]
=450÷[25×3]
=450÷75
=6
“[ ]”是什么符号?有什么作用呢?
探究新知
课堂练习
游戏(“凑24”)
6×(3-2)×4=24
(6+4-2)×3=24
(6+4÷2)×3=24
2×6+3×4=24
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
90-60÷15
(90-60)÷15
先算除法,60÷15的商是一位数,90减去这个数,差是80多
先算括号里的减法,90-60的差是30,再算除法,30除以15,商是2。
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
320÷40+20×2
320÷(40+20×2)
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
450÷(10+20)×3
450÷[(10+20)×3 ]
运算顺序是:加法→除法→乘法,括号里加法的计算结果是除数,除法的商再乘3,才是最后结果。
先算小括号里的加法,再算中括号里的乘法,用所得的积做除数,计算除法,除数大于前面的算式,商一定会变小。
课堂练习
2.四(1)班图书角有故事书128本,科技书52本。
班上男女生各18人平均每人可以分得多少本书?
(128+52)÷(18×2)
= 180 ÷ 36
= 5(本)
答:平均每人分得5本图书。
课堂练习
3. 156减去51与46的和,所得的差乘3,积是多少?
运算顺序该是怎样的?
答:积是177。
我知道,先算加法,再算减法,最后算乘法。
[156-(51+46)]×3
= [156-97]×3
= 59×3
= 177
先算小括号里面的加法,再算中括号里面的减法,最后算括号外面的乘法。
( )
[ ]
{ }
同学们,回忆下面这些符号,他们分别叫什么?
知识拓展
小括号
中括号
大括号
活动1 探究括号的由来
最早将“( )”印刷在书籍中,像现在一样使用的是德国数学家克拉维乌斯,他于1608年开始使用。
知识拓展
公元17世纪,“[ ]”第一次出现在英国人瓦里斯(1616-1703)的著作中。
活动1 探究括号的由来
知识拓展
大括号与小括号、中括号大概是同时出现的,以后我们会学习大括号,大括号用“{ }”表示。
活动1 探究括号的由来
知识拓展
课堂小结
1.只有加减法或者只有乘除法,从左向右依次计算。
2.既有加减又有乘除的算式,要先算乘除,后算加减。
3.有括号要先算括号里面的,如果既有小括号又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
四则混合运算(2)
复习导入
3.在四则混合运算中,只有加减法或只有乘除法,运算顺序是( )。
2.算式中带有括号的,应先算( ),再算( )。
1.在四则混合运算中,既有加减法又有乘除法,运算顺序是( )。
探究新知
师徒合作一小时做多少个?
还剩多少个没做?
还需要多少小时?
12+18=30(个)
147-27=120(个)
120 ÷ 30=4(时)
答:师徒合作还要4小时才能完成任务。
师徒共做147个零件。师傅做27个后,师徒合作还要多少时才能完成任务?
探究新知
综合算式:
(147-27) ÷(12+18)
师徒共做147个零件。师傅做27个后,师徒合作还要多少时才能完成任务?
算式中为什么要加两个小括号?
先算出师傅做了27个后还剩多少个。
还要先算出师徒二人每天共做多少个。
两个小括号,可以一块算,不分先和后。
最后用除法算还需要多少天,且要先算加法和减法,就必须加上小括号。
探究新知
1.说一说运算顺序,并计算。
(32+48)×(12 × 14)
(32+48)×(12 × 14)
=80 ×168
=13440
①
②
①
先算两个小括号里的加法和乘法,最后算括号外面的乘法。
探究新知
1.说一说运算顺序,并计算。
630 ÷ (15+15 × 5)
630 ÷ (15+15 × 5)
=630 ÷(15+75)
=630 ÷90
=7
①
②
先算小括号里的乘法和加法,最后算括号外面的除法。
③
探究新知
1.说一说运算顺序,并计算。
225-45 ×4
=225-180
=45
(225-45)×4
=180 ×4
=720
①
②
①
②
没有括号时,要先算乘法再算减法,当减法上加了小括号,就要先算减法再算乘法。运算顺序不同,计算的结果也不同。
254-250=4
22+29=51
4×51=
要想先算减法和加法,必须要加上小括号。
(254-250)×(22+29)
=4 × 51
=204
把下面的算式改写成一个综合算式。
探究新知
“[]”叫中括号。计算时要先算小括号里面的,再算中括号里面的。
450÷[(17+8)×3]
=450÷[25×3]
=450÷75
=6
“[ ]”是什么符号?有什么作用呢?
探究新知
课堂练习
游戏(“凑24”)
6×(3-2)×4=24
(6+4-2)×3=24
(6+4÷2)×3=24
2×6+3×4=24
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
90-60÷15
(90-60)÷15
先算除法,60÷15的商是一位数,90减去这个数,差是80多
先算括号里的减法,90-60的差是30,再算除法,30除以15,商是2。
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
320÷40+20×2
320÷(40+20×2)
课堂练习
1.不计算,判断每组中哪个算式的得数答,说说自己的想法。
450÷(10+20)×3
450÷[(10+20)×3 ]
运算顺序是:加法→除法→乘法,括号里加法的计算结果是除数,除法的商再乘3,才是最后结果。
先算小括号里的加法,再算中括号里的乘法,用所得的积做除数,计算除法,除数大于前面的算式,商一定会变小。
课堂练习
2.四(1)班图书角有故事书128本,科技书52本。
班上男女生各18人平均每人可以分得多少本书?
(128+52)÷(18×2)
= 180 ÷ 36
= 5(本)
答:平均每人分得5本图书。
课堂练习
3. 156减去51与46的和,所得的差乘3,积是多少?
运算顺序该是怎样的?
答:积是177。
我知道,先算加法,再算减法,最后算乘法。
[156-(51+46)]×3
= [156-97]×3
= 59×3
= 177
先算小括号里面的加法,再算中括号里面的减法,最后算括号外面的乘法。
( )
[ ]
{ }
同学们,回忆下面这些符号,他们分别叫什么?
知识拓展
小括号
中括号
大括号
活动1 探究括号的由来
最早将“( )”印刷在书籍中,像现在一样使用的是德国数学家克拉维乌斯,他于1608年开始使用。
知识拓展
公元17世纪,“[ ]”第一次出现在英国人瓦里斯(1616-1703)的著作中。
活动1 探究括号的由来
知识拓展
大括号与小括号、中括号大概是同时出现的,以后我们会学习大括号,大括号用“{ }”表示。
活动1 探究括号的由来
知识拓展
课堂小结
1.只有加减法或者只有乘除法,从左向右依次计算。
2.既有加减又有乘除的算式,要先算乘除,后算加减。
3.有括号要先算括号里面的,如果既有小括号又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的。
