§ 17 .1 勾股定理(2)
文档属性
| 名称 | § 17 .1 勾股定理(2) |
|
|
| 格式 | zip | ||
| 文件大小 | 31.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-28 00:00:00 | ||
图片预览

文档简介
§ 17.1 勾股定理(2)
备课人:
一、学习目标
通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
二、自助探究
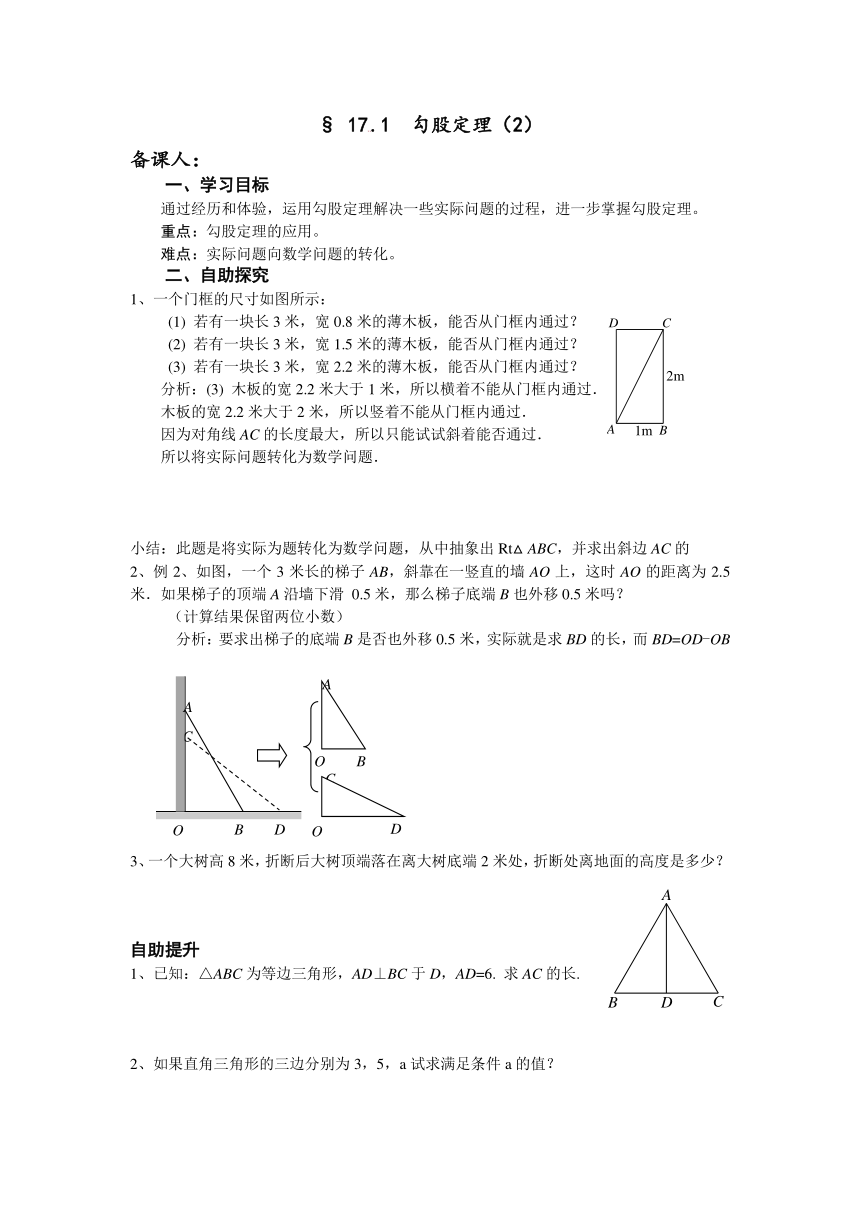
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.
木板的宽2.2米大于2米,所以竖着不能从门框内通过.
因为对角线AC的长度最大,所以只能试试斜着能否通过.
所以将实际问题转化为数学问题.
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的
2、例2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?
(计算结果保留两位小数)
分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB
3、一个大树高8米,折断后大树顶端落在离大树底端2米处,折断处离地面的高度是多少?
自助提升
1、已知:△ABC为等边三角形,AD⊥BC于D,AD=6. 求AC的长.
2、如果直角三角形的三边分别为3,5,a试求满足条件a的值?
3、以知正三角形ABC的边长为a,求△ABC的面积?
自助检测
1、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上
的高为 ( )
A、12 cm B、10 cm C、8 cm D、6 cm
2、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D。
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
3、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点
B处吃食,要爬行的最短路程(取3)是( )
A、20cm; B、10cm; C、14cm; D、无法确定.
4、若等腰直角三角形的斜边长为2,则它的直角边的长为 ,斜边上的高的长为 。
5、要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m,至少需要多长的梯子?(画出示意图)
6、小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
7、有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。谁的深度和这根芦苇的长度分别是多少?
O
B
D
CC
A
C
A
O
B
O
D
A
B
备课人:
一、学习目标
通过经历和体验,运用勾股定理解决一些实际问题的过程,进一步掌握勾股定理。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
二、自助探究
1、一个门框的尺寸如图所示:
(1) 若有一块长3米,宽0.8米的薄木板,能否从门框内通过?
(2) 若有一块长3米,宽1.5米的薄木板,能否从门框内通过?
(3) 若有一块长3米,宽2.2米的薄木板,能否从门框内通过?
分析:(3) 木板的宽2.2米大于1米,所以横着不能从门框内通过.
木板的宽2.2米大于2米,所以竖着不能从门框内通过.
因为对角线AC的长度最大,所以只能试试斜着能否通过.
所以将实际问题转化为数学问题.
小结:此题是将实际为题转化为数学问题,从中抽象出Rt△ABC,并求出斜边AC的
2、例2、如图,一个3米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5米.如果梯子的顶端A沿墙下滑 0.5米,那么梯子底端B也外移0.5米吗?
(计算结果保留两位小数)
分析:要求出梯子的底端B是否也外移0.5米,实际就是求BD的长,而BD=OD-OB
3、一个大树高8米,折断后大树顶端落在离大树底端2米处,折断处离地面的高度是多少?
自助提升
1、已知:△ABC为等边三角形,AD⊥BC于D,AD=6. 求AC的长.
2、如果直角三角形的三边分别为3,5,a试求满足条件a的值?
3、以知正三角形ABC的边长为a,求△ABC的面积?
自助检测
1、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上
的高为 ( )
A、12 cm B、10 cm C、8 cm D、6 cm
2、如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D。
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
3、如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点
B处吃食,要爬行的最短路程(取3)是( )
A、20cm; B、10cm; C、14cm; D、无法确定.
4、若等腰直角三角形的斜边长为2,则它的直角边的长为 ,斜边上的高的长为 。
5、要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m,至少需要多长的梯子?(画出示意图)
6、小明的叔叔家承包了一个矩形鱼池,已知其面积为48m2,其对角线长为10m,为建栅栏,要计算这个矩形鱼池的周长,你能帮助小明算一算吗?
7、有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。谁的深度和这根芦苇的长度分别是多少?
O
B
D
CC
A
C
A
O
B
O
D
A
B
