10.1.2 全等三角形性质与判定的综合应用同步练习(含答案)
文档属性
| 名称 | 10.1.2 全等三角形性质与判定的综合应用同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 13:35:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
1 全等三角形
第2课时 全等三角形性质与判定的综合应用
夯基础
1.如图,AB=DE,AC=DF,BC=EF,则∠D 等于 ( )
A.30° B.50° C.60° D.100°
2.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于 ( )
A.2.5 B.3 C.3.5 D.4
3.如图,已知AB=12,AB⊥BC于点B,AB⊥AD于点A,点E是CD的中点,连接AE并延长交BC于点F,AD=5,BC=10.则AE的长为( )
B.6 C.5
4.如图,点A,B,C,D在同一条直线上,△ACE≌△DBF,AD=11,BC=3,则AC= .
5.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
练能力
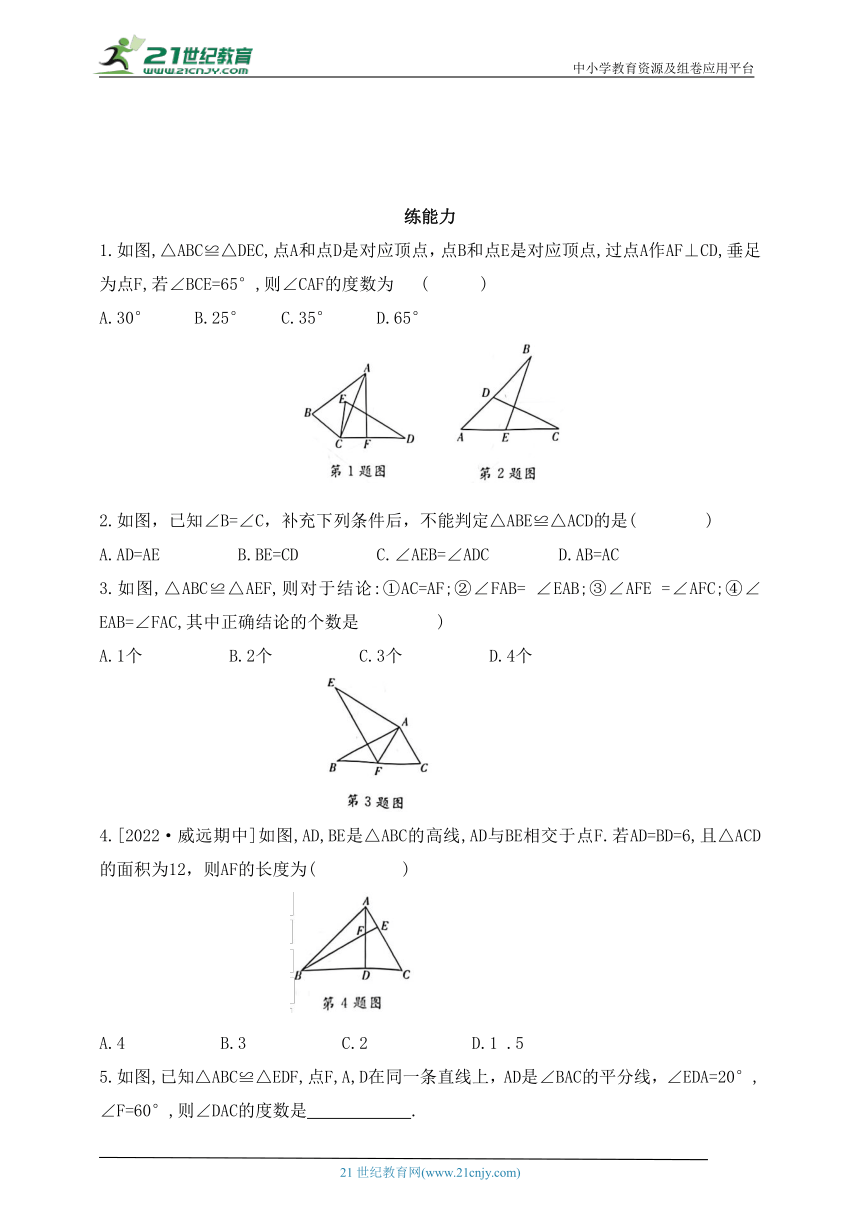
1.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为 ( )
A.30° B.25° C.35° D.65°
2.如图,已知∠B=∠C,补充下列条件后,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠AEB=∠ADC D.AB=AC
3.如图,△ABC≌△AEF,则对于结论:①AC=AF;②∠FAB= ∠EAB;③∠AFE =∠AFC;④∠EAB=∠FAC,其中正确结论的个数是 )
A.1个 B.2个 C.3个 D.4个
4.[2022·威远期中]如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1 .5
5.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是 .
6.如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),C的坐标为(4,3),如果存在点D,要使△ABD与△ABC全等,那么点D的坐标是 ___.
7.我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a,高为h的三角形的面积公式为想法是:以BC为边作矩形BCFE,点A在边FE上,再过点A作BC的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:
证明:用直尺和圆规过点A作BC的垂线AD交BC于点D.(只保留作图痕迹)
在△ADC和△CFA中,
∵AD⊥BC,∴∠ADC=90°.
∵∠F=90°,∴① .
∵EF∥BC,∴② .
又∵③ .∴△ADC≌△CFA(AAS).
同理可得④ .
8.已知:如图,AD,BF相交于O点,OA=OD,AB∥DF,点E,C在BF上,BE=CF.
(1)求证:△ABO≌△DFO;
(2)判断线段AC,DE的关系,并说明理由.
参考答案
夯基础
1 .D 2.B 3.A 4.7
5.解:∵∠BAD=∠EAC,∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD,
在△BAC与△EAD中, ∴△BAC≌△EAD(SAS),
∴∠D=∠C=50°.
练能力
1.B 2.C 3.C 4.C 5.50° 6.(4,-1)或(-1,3)或(-1,-1)
7.解:如图,AD即为所求.
在△ADC和△CFA中,
∵AD ⊥BC,∴∠ADC=90°.
∵∠F=90°,∴∠ADC=∠F.
∵EF∥BC,∴∠1=∠2.
又∵AC=CA.∴△ADC≌△CFA(AAS).
同理可得△ABD≌△BAE.
故答案为:∠ADC=∠F;∠1=∠2;AC=CA;△ABD≌△BAE.
8.解:(1)证明:∵AB∥DF,∴∠B=∠F,∠BAO=∠FDO,
在△ABO和△DFO中, ∴△ABO≌△DFO(AAS).
(2)AC=DE,AC∥DE.理由如下:
∵△ABO≌△DFO,∵BE=O/F,∴EO=CO,
在△AOC和△DOE中, ∴△AOC≌△DOE(SAS),
∴AC=DE,∠DAC=∠ADE,∴AC∥DE.
综上所述,AC=DE且AC∥DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
1 全等三角形
第2课时 全等三角形性质与判定的综合应用
夯基础
1.如图,AB=DE,AC=DF,BC=EF,则∠D 等于 ( )
A.30° B.50° C.60° D.100°
2.如图,AC⊥BE,DE⊥BE,若△ABC≌△BDE,AC=5,DE=2,则CE等于 ( )
A.2.5 B.3 C.3.5 D.4
3.如图,已知AB=12,AB⊥BC于点B,AB⊥AD于点A,点E是CD的中点,连接AE并延长交BC于点F,AD=5,BC=10.则AE的长为( )
B.6 C.5
4.如图,点A,B,C,D在同一条直线上,△ACE≌△DBF,AD=11,BC=3,则AC= .
5.如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
练能力
1.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为 ( )
A.30° B.25° C.35° D.65°
2.如图,已知∠B=∠C,补充下列条件后,不能判定△ABE≌△ACD的是( )
A.AD=AE B.BE=CD C.∠AEB=∠ADC D.AB=AC
3.如图,△ABC≌△AEF,则对于结论:①AC=AF;②∠FAB= ∠EAB;③∠AFE =∠AFC;④∠EAB=∠FAC,其中正确结论的个数是 )
A.1个 B.2个 C.3个 D.4个
4.[2022·威远期中]如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.4 B.3 C.2 D.1 .5
5.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是 .
6.如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(3,1),C的坐标为(4,3),如果存在点D,要使△ABD与△ABC全等,那么点D的坐标是 ___.
7.我们知道,矩形的面积等于这个矩形的长乘宽,小明想用其验证一个底为a,高为h的三角形的面积公式为想法是:以BC为边作矩形BCFE,点A在边FE上,再过点A作BC的垂线,将其转化为证三角形全等,由全等图形面积相等来得到验证.按以上思路完成下面的作图与填空:
证明:用直尺和圆规过点A作BC的垂线AD交BC于点D.(只保留作图痕迹)
在△ADC和△CFA中,
∵AD⊥BC,∴∠ADC=90°.
∵∠F=90°,∴① .
∵EF∥BC,∴② .
又∵③ .∴△ADC≌△CFA(AAS).
同理可得④ .
8.已知:如图,AD,BF相交于O点,OA=OD,AB∥DF,点E,C在BF上,BE=CF.
(1)求证:△ABO≌△DFO;
(2)判断线段AC,DE的关系,并说明理由.
参考答案
夯基础
1 .D 2.B 3.A 4.7
5.解:∵∠BAD=∠EAC,∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD,
在△BAC与△EAD中, ∴△BAC≌△EAD(SAS),
∴∠D=∠C=50°.
练能力
1.B 2.C 3.C 4.C 5.50° 6.(4,-1)或(-1,3)或(-1,-1)
7.解:如图,AD即为所求.
在△ADC和△CFA中,
∵AD ⊥BC,∴∠ADC=90°.
∵∠F=90°,∴∠ADC=∠F.
∵EF∥BC,∴∠1=∠2.
又∵AC=CA.∴△ADC≌△CFA(AAS).
同理可得△ABD≌△BAE.
故答案为:∠ADC=∠F;∠1=∠2;AC=CA;△ABD≌△BAE.
8.解:(1)证明:∵AB∥DF,∴∠B=∠F,∠BAO=∠FDO,
在△ABO和△DFO中, ∴△ABO≌△DFO(AAS).
(2)AC=DE,AC∥DE.理由如下:
∵△ABO≌△DFO,∵BE=O/F,∴EO=CO,
在△AOC和△DOE中, ∴△AOC≌△DOE(SAS),
∴AC=DE,∠DAC=∠ADE,∴AC∥DE.
综上所述,AC=DE且AC∥DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
