第十章 三角形的有关证明专项训练 全等三角形的常见模型(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明专项训练 全等三角形的常见模型(含答案) | 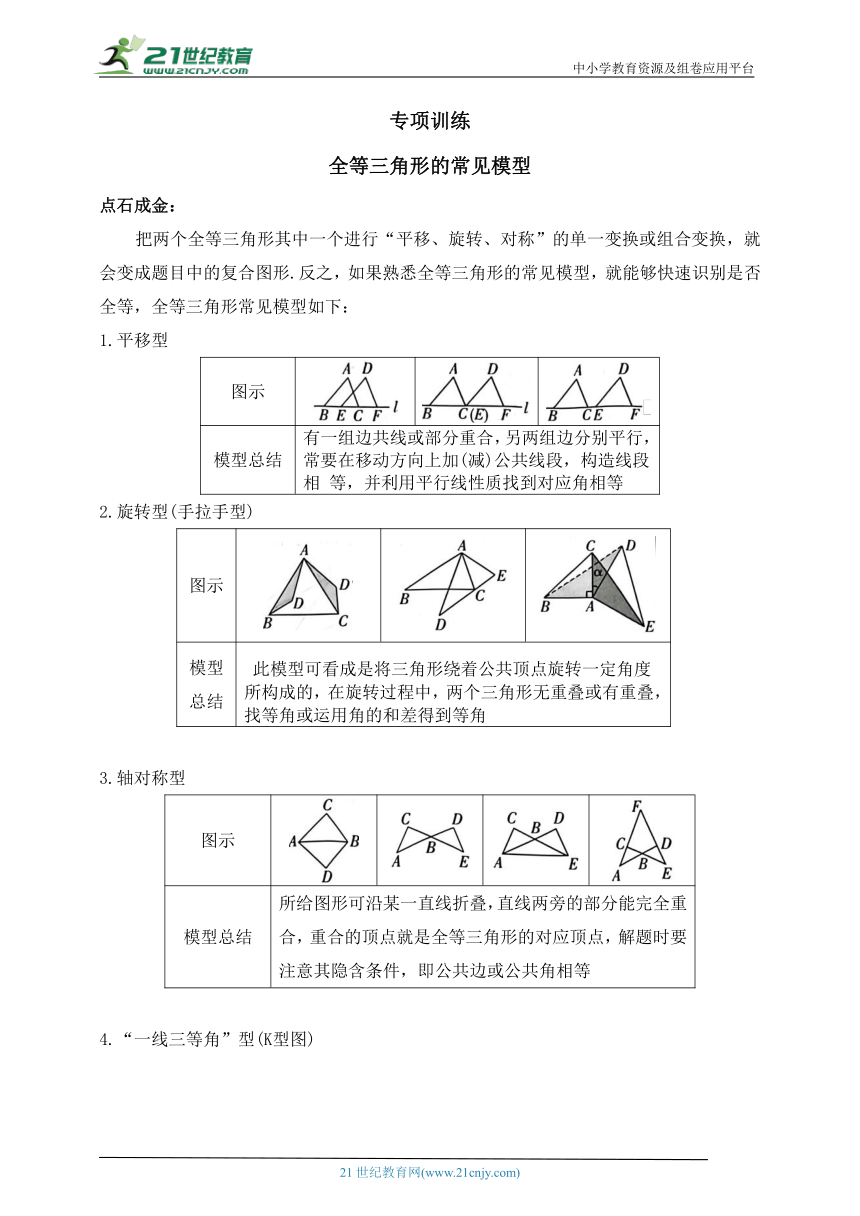 | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 13:35:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
全等三角形的常见模型
点石成金:
把两个全等三角形其中一个进行“平移、旋转、对称”的单一变换或组合变换,就会变成题目中的复合图形.反之,如果熟悉全等三角形的常见模型,就能够快速识别是否全等,全等三角形常见模型如下:
1.平移型
图示
模型总结 有一组边共线或部分重合,另两组边分别平行,常要在移动方向上加(减)公共线段,构造线段相 等,并利用平行线性质找到对应角相等
2.旋转型(手拉手型)
图示
模型 总结 此模型可看成是将三角形绕着公共顶点旋转一定角度所构成的,在旋转过程中,两个三角形无重叠或有重叠,找等角或运用角的和差得到等角
3.轴对称型
图示
模型总结 所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等
4.“一线三等角”型(K型图)
图示
模型 总结 三个等角(∠A=∠CPD=∠B),称“一线三等角”模型(角度为锐角、钝角),若等角为直角称“一线三垂直”
模型① 平移型
1.如图,AB∥CD,点C是BE 的中点,直接应用“ASA”定理证明△ABC≌△DCE 还需要的条件是 ( )
A.AB=CD B.∠ACB=∠E C.∠A=∠D D.AC=DE
2.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF.有下列三个条件:①AC=DF,②∠ABC=∠DEF,③∠ACB=∠DFE.
(1)请在上述三个条件中选取一个条件,使得△ABC≌△DEF.
你选取的条件为(填写序号) (只需选一个条件,多选不得分),你判定△ABC≌△DEF的依据是 .(填“SSS”或“SAS”或“ASA”或“AAS”)
(2)利用(1)的结论△ABC≌△DEF.求证:AB∥DE.
模型② 旋转型
3.如图,CA=CD,∠ACD=∠BCE,请添加一个条件 ,使△ABC≌△DEC.
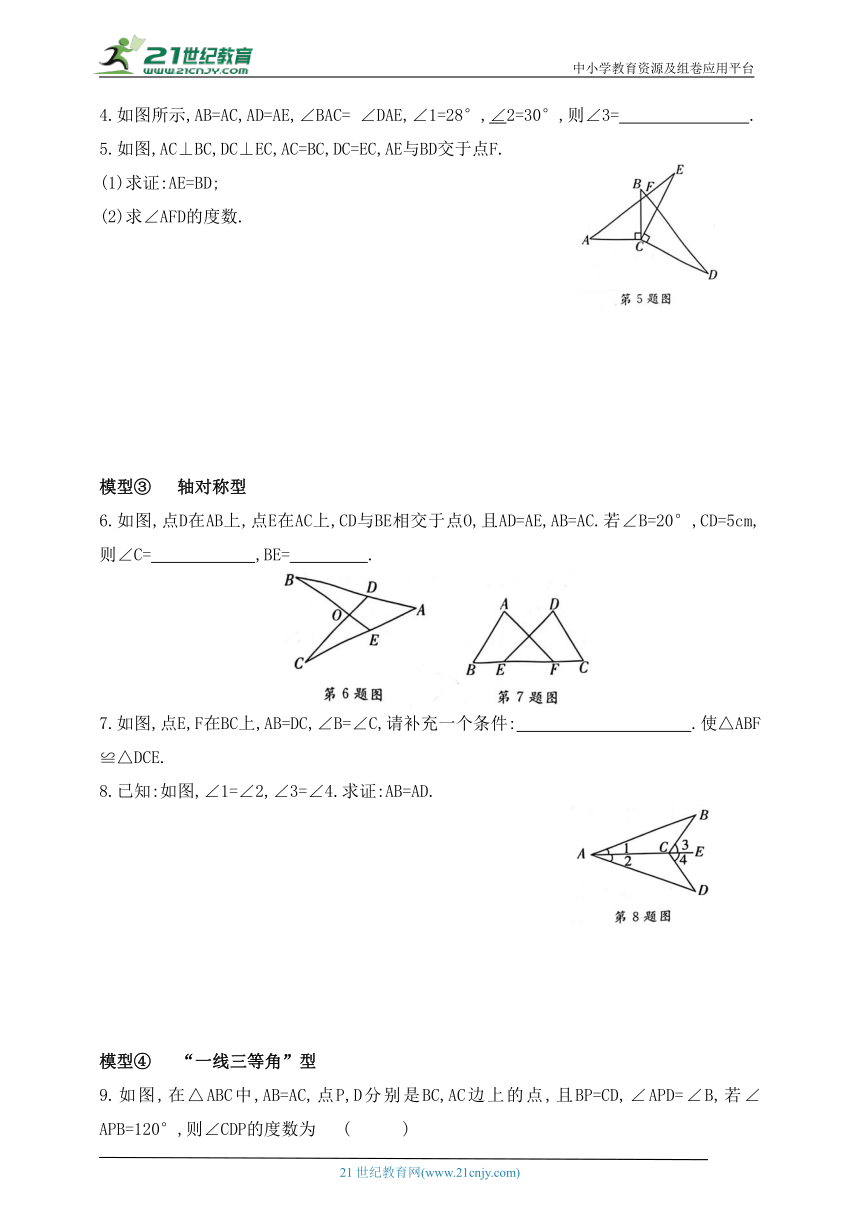
4.如图所示,AB=AC,AD=AE,∠BAC= ∠DAE,∠1=28°,∠2=30°,则∠3= .
5.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
模型③ 轴对称型
6.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .
7.如图,点E,F在BC上,AB=DC,∠B=∠C,请补充一个条件: .使△ABF≌△DCE.
8.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.
模型④ “一线三等角”型
9.如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且BP=CD,∠APD=∠B,若∠APB=120°,则∠CDP的度数为 ( )
A.30° B.60° C.120° D.150°
10.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A 和B,AD,BC的长表示两个工厂到河岸的距离,其中E是进水口,D,C为污水净化后的出口.已知AE=BE,∠AEB=90°,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
参考答案
1.B
2.解:(1)(示例)在△ABC和△DEF中, ∴△ABC≌△DEF(SSS),
故答案为:①,SSS;
(2)证明:∵△ABC≌△DEF,∴∠A=∠EDF,∴AB∥DE.
3.(示例)∠A=∠D 4.58°
5.解:(1)∵AC⊥BC,DC⊥EC,∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.即∠ACE=∠BCD.
又∵AC=BC,EC=DC,
在△ACE与△BCD中 ∴△ACE≌△BCD(SAS).
∴AE=BD.
(2)设AE与BC交于O点,则∠AOC=∠BOF,
∵△ACE≌△BCD,∴∠A=∠B.
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°.
∴∠BFO=∠ACO=90°.∴∠AFD=180°-∠BFO=90°.
6.20° 5cm 7.(示例)BE=CF
8.证明:∵∠3=∠4,∴∠ACB=∠ACD,
在△ACB和△ACD中, ∴△ACB≌△ACD(ASA),
∴AB=AD.
9.C
10.解:由题意,得AD⊥CD,BC⊥CD,∴∠ADE=∠ECB=90°,∴∠AED+∠DAE=90°,
∵∠AEB=90°,∴∠AED+∠CEB=90°,∴∠DAE=∠CEB,
在△ADE与△ECB中, ∴△ADE≌△ECB(AAS),∴AD=CE,DE=BC,
∵AD=150米,BC=350米,∴DC=DE+CE=BC+AD=350+150=500(米),
答:两个排污口之间的水平距离DC为500米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
全等三角形的常见模型
点石成金:
把两个全等三角形其中一个进行“平移、旋转、对称”的单一变换或组合变换,就会变成题目中的复合图形.反之,如果熟悉全等三角形的常见模型,就能够快速识别是否全等,全等三角形常见模型如下:
1.平移型
图示
模型总结 有一组边共线或部分重合,另两组边分别平行,常要在移动方向上加(减)公共线段,构造线段相 等,并利用平行线性质找到对应角相等
2.旋转型(手拉手型)
图示
模型 总结 此模型可看成是将三角形绕着公共顶点旋转一定角度所构成的,在旋转过程中,两个三角形无重叠或有重叠,找等角或运用角的和差得到等角
3.轴对称型
图示
模型总结 所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等
4.“一线三等角”型(K型图)
图示
模型 总结 三个等角(∠A=∠CPD=∠B),称“一线三等角”模型(角度为锐角、钝角),若等角为直角称“一线三垂直”
模型① 平移型
1.如图,AB∥CD,点C是BE 的中点,直接应用“ASA”定理证明△ABC≌△DCE 还需要的条件是 ( )
A.AB=CD B.∠ACB=∠E C.∠A=∠D D.AC=DE
2.如图,点A,D,C,F在同一条直线上,AB=DE,BC=EF.有下列三个条件:①AC=DF,②∠ABC=∠DEF,③∠ACB=∠DFE.
(1)请在上述三个条件中选取一个条件,使得△ABC≌△DEF.
你选取的条件为(填写序号) (只需选一个条件,多选不得分),你判定△ABC≌△DEF的依据是 .(填“SSS”或“SAS”或“ASA”或“AAS”)
(2)利用(1)的结论△ABC≌△DEF.求证:AB∥DE.
模型② 旋转型
3.如图,CA=CD,∠ACD=∠BCE,请添加一个条件 ,使△ABC≌△DEC.
4.如图所示,AB=AC,AD=AE,∠BAC= ∠DAE,∠1=28°,∠2=30°,则∠3= .
5.如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)求证:AE=BD;
(2)求∠AFD的度数.
模型③ 轴对称型
6.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .
7.如图,点E,F在BC上,AB=DC,∠B=∠C,请补充一个条件: .使△ABF≌△DCE.
8.已知:如图,∠1=∠2,∠3=∠4.求证:AB=AD.
模型④ “一线三等角”型
9.如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且BP=CD,∠APD=∠B,若∠APB=120°,则∠CDP的度数为 ( )
A.30° B.60° C.120° D.150°
10.如图是一个工业开发区局部的设计图,河的同一侧有两个工厂A 和B,AD,BC的长表示两个工厂到河岸的距离,其中E是进水口,D,C为污水净化后的出口.已知AE=BE,∠AEB=90°,AD=150米,BC=350米,求两个排污口之间的水平距离DC.
参考答案
1.B
2.解:(1)(示例)在△ABC和△DEF中, ∴△ABC≌△DEF(SSS),
故答案为:①,SSS;
(2)证明:∵△ABC≌△DEF,∴∠A=∠EDF,∴AB∥DE.
3.(示例)∠A=∠D 4.58°
5.解:(1)∵AC⊥BC,DC⊥EC,∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE.即∠ACE=∠BCD.
又∵AC=BC,EC=DC,
在△ACE与△BCD中 ∴△ACE≌△BCD(SAS).
∴AE=BD.
(2)设AE与BC交于O点,则∠AOC=∠BOF,
∵△ACE≌△BCD,∴∠A=∠B.
∴∠A+∠AOC+∠ACO=∠B+∠BOF+∠BFO=180°.
∴∠BFO=∠ACO=90°.∴∠AFD=180°-∠BFO=90°.
6.20° 5cm 7.(示例)BE=CF
8.证明:∵∠3=∠4,∴∠ACB=∠ACD,
在△ACB和△ACD中, ∴△ACB≌△ACD(ASA),
∴AB=AD.
9.C
10.解:由题意,得AD⊥CD,BC⊥CD,∴∠ADE=∠ECB=90°,∴∠AED+∠DAE=90°,
∵∠AEB=90°,∴∠AED+∠CEB=90°,∴∠DAE=∠CEB,
在△ADE与△ECB中, ∴△ADE≌△ECB(AAS),∴AD=CE,DE=BC,
∵AD=150米,BC=350米,∴DC=DE+CE=BC+AD=350+150=500(米),
答:两个排污口之间的水平距离DC为500米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
