3.6.2 圆的切线判定和三角形的内切圆 课件(共30张PPT)
文档属性
| 名称 | 3.6.2 圆的切线判定和三角形的内切圆 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-15 13:18:53 | ||
图片预览






文档简介
(共30张PPT)
3.6.2 圆的切线判定和三角形的内切圆
北师大版 九年级 下册
教学目标
教学目标:1.理解并掌握切线的判定定理,能够熟练运用切线的性质和判定
解决有关的证明和计算.
2.了解三角形的内切圆的有关概念及性质并能灵活应用.
教学重点:1.探索圆的切线的判定方法,并能运用.
2.作三角形内切圆的方法.
教学难点:探索圆的切线的判定方法.
新知讲解
情境引入
当你在下雨天快速转动雨伞时,水滴是顺着伞的什么方向飞出去的?
砂轮打磨零件时,溅出火星沿着砂轮的什么方向飞出去的
均沿着圆的切线的方向飞出.
B
●O
A
┓
d
α
┏
d
α
d
┓
l
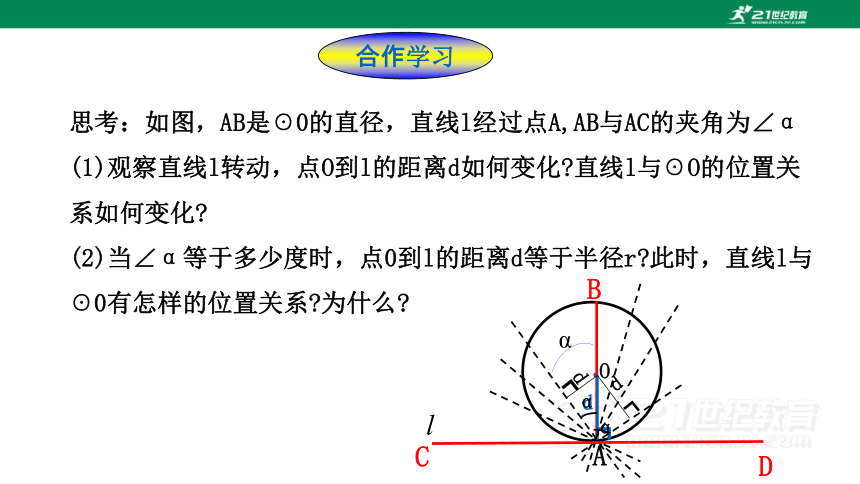
思考:如图,AB是☉0的直径,直线l经过点A,AB与AC的夹角为∠α
(1)观察直线l转动,点O到l的距离d如何变化 直线l与☉O的位置关系如何变化
(2)当∠α等于多少度时,点0到l的距离d等于半径r 此时,直线l与☉0有怎样的位置关系 为什么
C
D
α
合作学习
(1)随着∠α的变化,点O到l的距离d如何变
化?直线l 与⊙O的位置关系如何变化?
∠α 越小,点O到 l 的距离d越小;
∠α=90°时,直线 l 与⊙O相切;
∠α<90°时,直线 l 与⊙O相交.
(2)当∠α等于多少度时,点O到l的距离d等
于半径r?此时,直线l与⊙O有怎样的位置关系?为什么?
∠α=90°时,点O到l的距离d等于半径 r;
此时,直线l与⊙O相切.
由此可得到一个结论:
过半径外端且垂直于半径的直线是圆的切线.
提炼概念
O
A
B
C
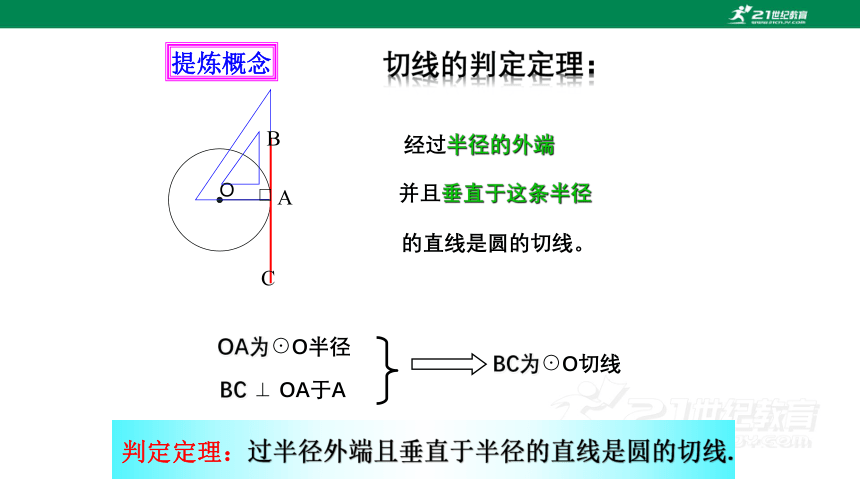
经过半径的外端
并且垂直于这条半径
的直线是圆的切线。
切线的判定定理:
OA为⊙O半径
BC ⊥ OA于A
BC为⊙O切线
判定定理:过半径外端且垂直于半径的直线是圆的切线.
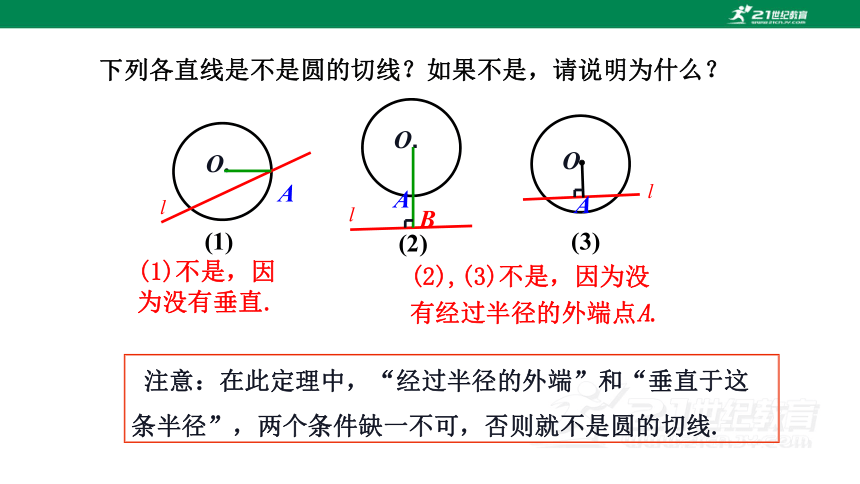
下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
注意:在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
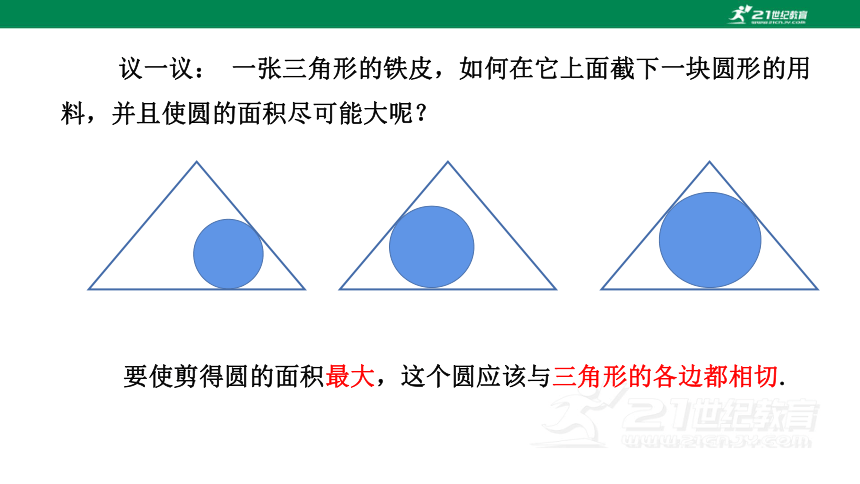
议一议: 一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
要使剪得圆的面积最大,这个圆应该与三角形的各边都相切.
典例精讲
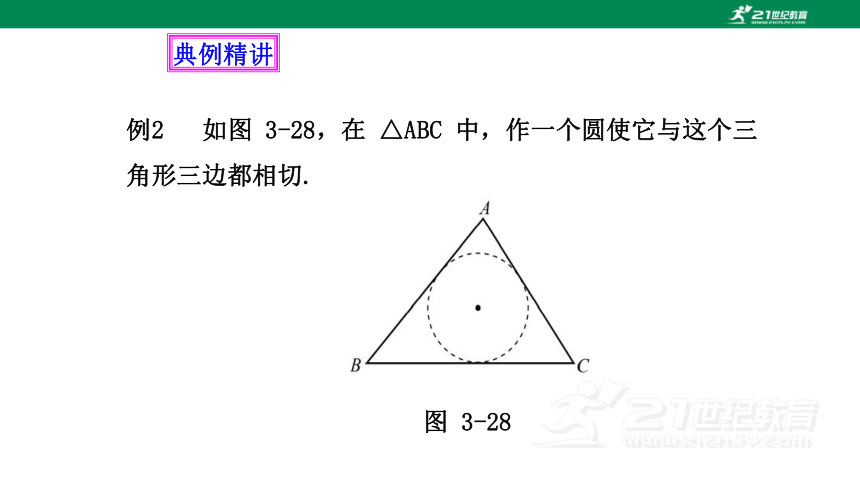
例2 如图 3-28,在 △ABC 中,作一个圆使它与这个三角形三边都相切.
图 3-28
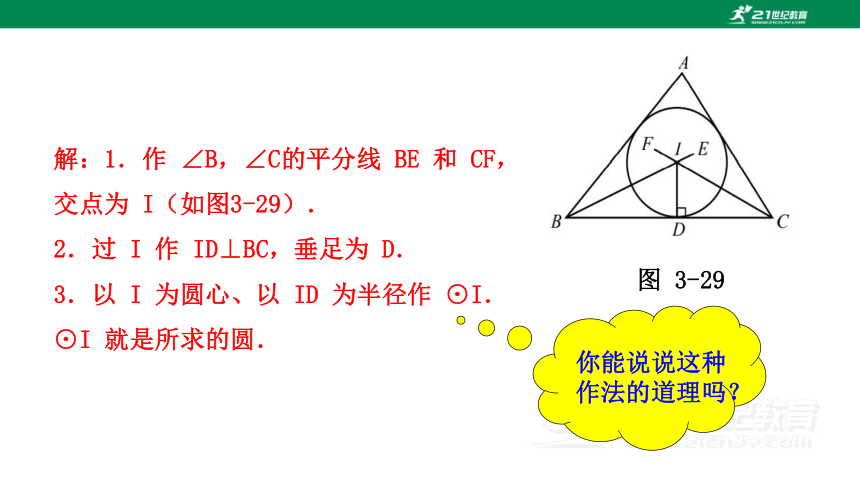
图 3-29
解:1.作 ∠B,∠C的平分线 BE 和 CF,交点为 I(如图3-29).
2.过 I 作 ID⊥BC,垂足为 D.
3.以 I 为圆心、以 ID 为半径作 ⊙I.
⊙I 就是所求的圆.
你能说说这种作法的道理吗?
由例 2 的作图过程可知,BE 和 CF 只有一个
交点 I,并且 I 到△ABC 三边的距离相等,因此
和三角形三边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆(inscribed circle of triangle),
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心(incenter).
归纳概念
图形 ⊙O 的名称 △ABC 的名称 圆心O 的确定 “心”的性质 “心”的位置
△ABC的内切圆 ⊙O 的外切三角形 三角形三条角平分线的交点 到三角形的三条边的距离相等 一定在三角形内部
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
课堂练习
1、下列命题中正确的是( )
A. 与圆有公共点的直线是圆的切线
B. 经过半径外端点且与这条半径垂直的直线是圆的直径
C. 垂直于圆的半径的直线是圆的切线
D. 到圆心的距离等于圆的半径的直线是圆的切线
D
2.如图,△ABC是⊙O的内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠EAB=∠BAC
C.EF⊥AC
D.AC是⊙O的直径
A
3.如图,已知锐角三角形、直角三角形、钝角三角形,分别作出它们的内切圆.三角形的内心是否都在三角形内部?
解:图略.三角形的内心都在三角形的内部.
锐角三角形
直角三角形
钝角三角形
4.△ABC中,☉O是△ABC的内切圆,∠A=70°,求∠BOC的度数.
A
B
C
O
解:∵∠ A=70°
∴∠ABC+∠ACB=180°-∠ A=110°
∵☉O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
即∠ OBC= ∠ABC ∠OCB= ∠ACB
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- ( ∠ABC +∠ACB)
=180°- ×110°
= 125°.
A
B
C
O
·
B
D
E
F
O
C
A
5.如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
解:设△ABC的内切圆与三边相切于D、E、F,
连接OA、OB、OC、OD、OE、OF,
则OD⊥AB,OE⊥BC,OF⊥AC.
∴S△ABC=S△AOB+S△BOC +S△AOC
= AB·OD+ BC·OE+ AC·OF
= l·r
6.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB延长线交于点F,若∠CDE=∠DAC,AC=12.
(1)求⊙O半径;
(2)求证:DE为⊙O的切线.
解:(1)∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵BD=CD,
∴AB=AC=12,
∴⊙O半径为6;
(2)证明:连接OD,
∵∠CDE=∠DAC,
∴∠CDE+∠C=∠DAC+∠C,
∴∠AED=∠ADB,
由(1)知∠ADB=90°,
∴∠AED=90°,
∵DC=BD,OA=OB
∴OD//AC.
∴∠ODF=∠AED=90°,
∴半径OD⊥EF.
∴DE为⊙O的切线.
如果用小圆代表
你们学到的知识,
用大圆代表我学到
的知识,那么大圆
的面积是多一点,但
两圆之外的空白都
是我们的无知面.圆越
大其圆周接触的无知面就多.
——古希腊 芝诺
课堂总结
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
三角形内切圆
有关概念
内心概念及性质
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.6.2 圆的切线判定和三角形的内切圆
北师大版 九年级 下册
教学目标
教学目标:1.理解并掌握切线的判定定理,能够熟练运用切线的性质和判定
解决有关的证明和计算.
2.了解三角形的内切圆的有关概念及性质并能灵活应用.
教学重点:1.探索圆的切线的判定方法,并能运用.
2.作三角形内切圆的方法.
教学难点:探索圆的切线的判定方法.
新知讲解
情境引入
当你在下雨天快速转动雨伞时,水滴是顺着伞的什么方向飞出去的?
砂轮打磨零件时,溅出火星沿着砂轮的什么方向飞出去的
均沿着圆的切线的方向飞出.
B
●O
A
┓
d
α
┏
d
α
d
┓
l
思考:如图,AB是☉0的直径,直线l经过点A,AB与AC的夹角为∠α
(1)观察直线l转动,点O到l的距离d如何变化 直线l与☉O的位置关系如何变化
(2)当∠α等于多少度时,点0到l的距离d等于半径r 此时,直线l与☉0有怎样的位置关系 为什么
C
D
α
合作学习
(1)随着∠α的变化,点O到l的距离d如何变
化?直线l 与⊙O的位置关系如何变化?
∠α 越小,点O到 l 的距离d越小;
∠α=90°时,直线 l 与⊙O相切;
∠α<90°时,直线 l 与⊙O相交.
(2)当∠α等于多少度时,点O到l的距离d等
于半径r?此时,直线l与⊙O有怎样的位置关系?为什么?
∠α=90°时,点O到l的距离d等于半径 r;
此时,直线l与⊙O相切.
由此可得到一个结论:
过半径外端且垂直于半径的直线是圆的切线.
提炼概念
O
A
B
C
经过半径的外端
并且垂直于这条半径
的直线是圆的切线。
切线的判定定理:
OA为⊙O半径
BC ⊥ OA于A
BC为⊙O切线
判定定理:过半径外端且垂直于半径的直线是圆的切线.
下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
注意:在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
议一议: 一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
要使剪得圆的面积最大,这个圆应该与三角形的各边都相切.
典例精讲
例2 如图 3-28,在 △ABC 中,作一个圆使它与这个三角形三边都相切.
图 3-28
图 3-29
解:1.作 ∠B,∠C的平分线 BE 和 CF,交点为 I(如图3-29).
2.过 I 作 ID⊥BC,垂足为 D.
3.以 I 为圆心、以 ID 为半径作 ⊙I.
⊙I 就是所求的圆.
你能说说这种作法的道理吗?
由例 2 的作图过程可知,BE 和 CF 只有一个
交点 I,并且 I 到△ABC 三边的距离相等,因此
和三角形三边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆(inscribed circle of triangle),
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心(incenter).
归纳概念
图形 ⊙O 的名称 △ABC 的名称 圆心O 的确定 “心”的性质 “心”的位置
△ABC的内切圆 ⊙O 的外切三角形 三角形三条角平分线的交点 到三角形的三条边的距离相等 一定在三角形内部
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
l
A
l
O
l
r
d
课堂练习
1、下列命题中正确的是( )
A. 与圆有公共点的直线是圆的切线
B. 经过半径外端点且与这条半径垂直的直线是圆的直径
C. 垂直于圆的半径的直线是圆的切线
D. 到圆心的距离等于圆的半径的直线是圆的切线
D
2.如图,△ABC是⊙O的内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C
B.∠EAB=∠BAC
C.EF⊥AC
D.AC是⊙O的直径
A
3.如图,已知锐角三角形、直角三角形、钝角三角形,分别作出它们的内切圆.三角形的内心是否都在三角形内部?
解:图略.三角形的内心都在三角形的内部.
锐角三角形
直角三角形
钝角三角形
4.△ABC中,☉O是△ABC的内切圆,∠A=70°,求∠BOC的度数.
A
B
C
O
解:∵∠ A=70°
∴∠ABC+∠ACB=180°-∠ A=110°
∵☉O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
即∠ OBC= ∠ABC ∠OCB= ∠ACB
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- ( ∠ABC +∠ACB)
=180°- ×110°
= 125°.
A
B
C
O
·
B
D
E
F
O
C
A
5.如图,△ABC的内切圆的半径为r, △ABC的周长为l,求△ABC的面积S.
解:设△ABC的内切圆与三边相切于D、E、F,
连接OA、OB、OC、OD、OE、OF,
则OD⊥AB,OE⊥BC,OF⊥AC.
∴S△ABC=S△AOB+S△BOC +S△AOC
= AB·OD+ BC·OE+ AC·OF
= l·r
6.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,E为AC上一点,直线ED与AB延长线交于点F,若∠CDE=∠DAC,AC=12.
(1)求⊙O半径;
(2)求证:DE为⊙O的切线.
解:(1)∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又∵BD=CD,
∴AB=AC=12,
∴⊙O半径为6;
(2)证明:连接OD,
∵∠CDE=∠DAC,
∴∠CDE+∠C=∠DAC+∠C,
∴∠AED=∠ADB,
由(1)知∠ADB=90°,
∴∠AED=90°,
∵DC=BD,OA=OB
∴OD//AC.
∴∠ODF=∠AED=90°,
∴半径OD⊥EF.
∴DE为⊙O的切线.
如果用小圆代表
你们学到的知识,
用大圆代表我学到
的知识,那么大圆
的面积是多一点,但
两圆之外的空白都
是我们的无知面.圆越
大其圆周接触的无知面就多.
——古希腊 芝诺
课堂总结
切线的
判定方法
定义法
数量关系法
判定定理
1个公共点,则相切
d=r,则相切
经过半径的外端并且垂直于这条半径的直线是圆的切线
证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径.
三角形内切圆
有关概念
内心概念及性质
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
