2013---2014学年度第2学期期中 7年级数学试题检测三青岛版(无答案)
文档属性
| 名称 | 2013---2014学年度第2学期期中 7年级数学试题检测三青岛版(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-27 00:00:00 | ||
图片预览

文档简介
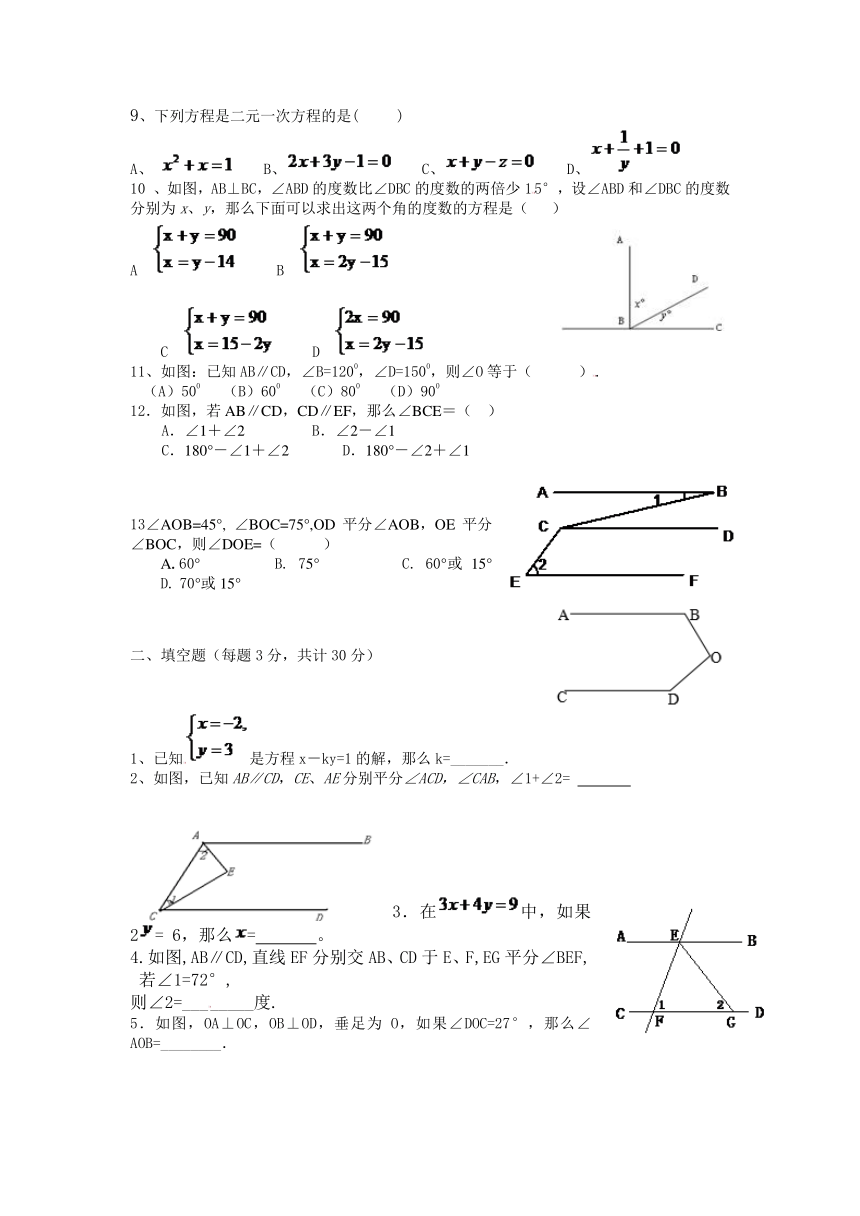
2013-2014学年度第二学期期中试题
七年级数学检测三
一、选择题(每小题3分,共计36分)请把正确答案的序号填入表中
1.下列图形中,可用么∠1,∠AOB,∠O三种方法表示同一个角的是( )
2.如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是( )
A.∠AOB>∠DOC B.∠AOB<∠DOC C.∠AOB=∠DOC D.无法比较
3、下面四个图形中,∠1与∠2是对顶角的图形( )
A、1个 B、2个 C、3个 D、4个
4.如图,下列说法中正确的是( )
A.∠1与∠C是同位角 B.∠1与∠3是同旁内角
C.∠3与∠C是内错角 D.∠1与∠3是对顶角
5.如图,根据下列条件,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
6.解方程组时,某同学把看错后得到,而正确的解是,那么的值是( )
A. B.不能确定,
C. D.的值不能确定
7.如图,AB∥CD,∠B=23°,∠D=42°,则∠E=( )
A.23° B.42° C.65° D.19°
8、如图,直线a∥b,直线c是截线,如果∠1=50°,
那么∠2等于( )
A、50°B、150° C、140° D、130°
9、下列方程是二元一次方程的是( )
A、 B、 C、 D、
10 、如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,设∠ABD和∠DBC的度数分别为x、y,那么下面可以求出这两个角的度数的方程是( )
A B
C D
11、如图:已知AB∥CD,∠B=1200,∠D=1500,则∠O等于( ).
(A)500 (B)600 (C)800 (D)900
12.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2-∠1
C.180°-∠1+∠2 D.180°-∠2+∠1
13∠AOB=45°, ∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE=( )
A.60° B. 75° C. 60°或15° D. 70°或15°
二、填空题(每题3分,共计30分)
1、已知是方程x-ky=1的解,那么k=_______.
2、如图,已知AB∥CD,CE、AE分别平分∠ACD,∠CAB,∠1+∠2=
3.在中,如果2= 6,那么= 。
4.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,
则∠2=________度.
5.如图,OA⊥OC,OB⊥OD,垂足为O,如果∠DOC=27°,那么∠AOB=________.
6.如图所示,若∠A+∠2+∠3=180°,则可以判定哪两条直线平行 __________
7.如图所示,直线a∥b,c∥d,∠1=106°,则∠3=________.
8.若方程组的解中与的值相等,则a的值为________.
9.已知方程组的解是,则的解是_______.
10、方程是二元一次方程,则,
三、解答题:(解答要求步骤完整,格式规范,共66分)
1、解下列方程组(每小题5分,共10分):
(1) (2)
2、(8分)如图,已知DF∥AC,∠C=∠D,你能判断CE∥BD吗?试说明理由。
3. (8分)如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°,求∠DAE的度数.
4、(10分)已知方程组 的解x、互为相反数,求m的值。
5(10分)一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表所示
第一次 第二次
甲种货车辆数(单位:辆) 2 5
乙种货车辆数(单位:辆) 3 6
累计运货物吨数(单位:吨) 15.5 35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
6 已知方程组的解能使等式成立,求的值.
7(本题满分8分)如下图所示,已知点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,
求证:∠A=∠F
8.(10分)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,若果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节的条件限制,公司必须在15天内将这些蔬菜全部销售或加工完毕,为此公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上销售;
方案三:将部分蔬菜进行粗加工,其余蔬菜进行精加工,并恰好在15天内完成。
你认为选择哪种方案获利最多?为什么?
七年级数学检测三
一、选择题(每小题3分,共计36分)请把正确答案的序号填入表中
1.下列图形中,可用么∠1,∠AOB,∠O三种方法表示同一个角的是( )
2.如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是( )
A.∠AOB>∠DOC B.∠AOB<∠DOC C.∠AOB=∠DOC D.无法比较
3、下面四个图形中,∠1与∠2是对顶角的图形( )
A、1个 B、2个 C、3个 D、4个
4.如图,下列说法中正确的是( )
A.∠1与∠C是同位角 B.∠1与∠3是同旁内角
C.∠3与∠C是内错角 D.∠1与∠3是对顶角
5.如图,根据下列条件,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
6.解方程组时,某同学把看错后得到,而正确的解是,那么的值是( )
A. B.不能确定,
C. D.的值不能确定
7.如图,AB∥CD,∠B=23°,∠D=42°,则∠E=( )
A.23° B.42° C.65° D.19°
8、如图,直线a∥b,直线c是截线,如果∠1=50°,
那么∠2等于( )
A、50°B、150° C、140° D、130°
9、下列方程是二元一次方程的是( )
A、 B、 C、 D、
10 、如图,AB⊥BC,∠ABD的度数比∠DBC的度数的两倍少15°,设∠ABD和∠DBC的度数分别为x、y,那么下面可以求出这两个角的度数的方程是( )
A B
C D
11、如图:已知AB∥CD,∠B=1200,∠D=1500,则∠O等于( ).
(A)500 (B)600 (C)800 (D)900
12.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2-∠1
C.180°-∠1+∠2 D.180°-∠2+∠1
13∠AOB=45°, ∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE=( )
A.60° B. 75° C. 60°或15° D. 70°或15°
二、填空题(每题3分,共计30分)
1、已知是方程x-ky=1的解,那么k=_______.
2、如图,已知AB∥CD,CE、AE分别平分∠ACD,∠CAB,∠1+∠2=
3.在中,如果2= 6,那么= 。
4.如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,
则∠2=________度.
5.如图,OA⊥OC,OB⊥OD,垂足为O,如果∠DOC=27°,那么∠AOB=________.
6.如图所示,若∠A+∠2+∠3=180°,则可以判定哪两条直线平行 __________
7.如图所示,直线a∥b,c∥d,∠1=106°,则∠3=________.
8.若方程组的解中与的值相等,则a的值为________.
9.已知方程组的解是,则的解是_______.
10、方程是二元一次方程,则,
三、解答题:(解答要求步骤完整,格式规范,共66分)
1、解下列方程组(每小题5分,共10分):
(1) (2)
2、(8分)如图,已知DF∥AC,∠C=∠D,你能判断CE∥BD吗?试说明理由。
3. (8分)如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=40°,∠C=60°,求∠DAE的度数.
4、(10分)已知方程组 的解x、互为相反数,求m的值。
5(10分)一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表所示
第一次 第二次
甲种货车辆数(单位:辆) 2 5
乙种货车辆数(单位:辆) 3 6
累计运货物吨数(单位:吨) 15.5 35
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
6 已知方程组的解能使等式成立,求的值.
7(本题满分8分)如下图所示,已知点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,
求证:∠A=∠F
8.(10分)某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,若果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节的条件限制,公司必须在15天内将这些蔬菜全部销售或加工完毕,为此公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上销售;
方案三:将部分蔬菜进行粗加工,其余蔬菜进行精加工,并恰好在15天内完成。
你认为选择哪种方案获利最多?为什么?
同课章节目录
