10.3.2 “HL”定理同步练习(含答案)
文档属性
| 名称 | 10.3.2 “HL”定理同步练习(含答案) | 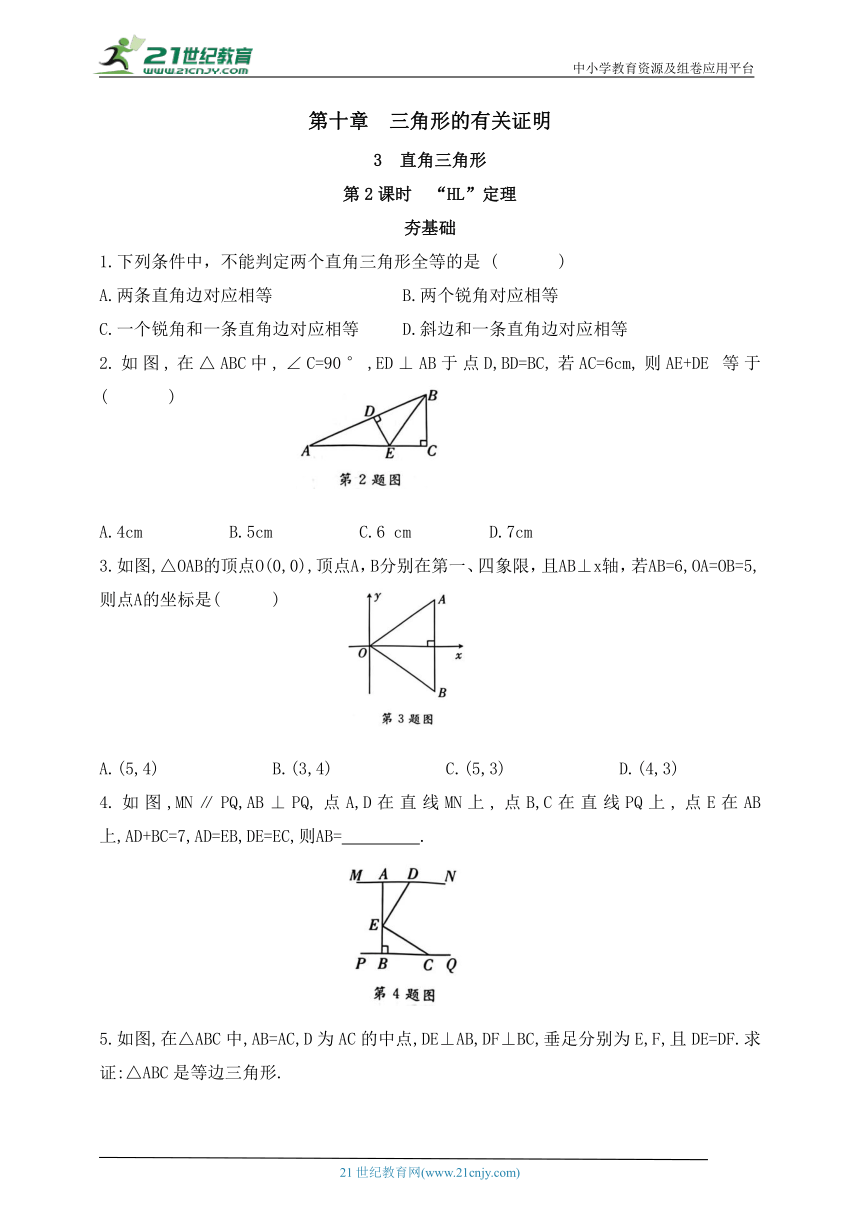 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 13:35:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
3 直角三角形
第2课时 “HL”定理
夯基础
1.下列条件中,不能判定两个直角三角形全等的是 ( )
A.两条直角边对应相等 B.两个锐角对应相等
C.一个锐角和一条直角边对应相等 D.斜边和一条直角边对应相等
2.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6cm,则AE+DE 等于 ( )
A.4cm B.5cm C.6 cm D.7cm
3.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A.(5,4) B.(3,4) C.(5,3) D.(4,3)
4.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB 上,AD+BC=7,AD=EB,DE=EC,则AB= .
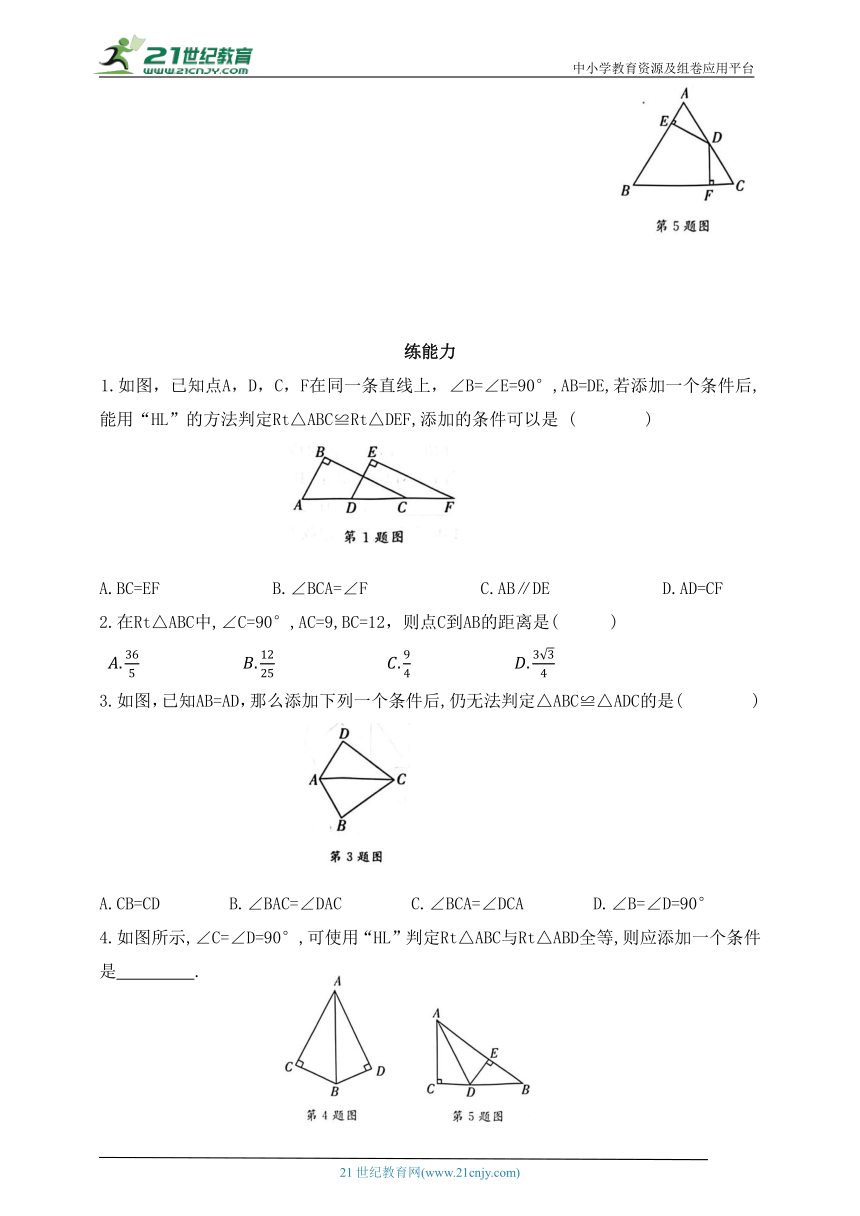
5.如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为E,F,且DE=DF.求证:△ABC是等边三角形.
练能力
1.如图,已知点A,D,C,F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是 ( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
2.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
3.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
4.如图所示,∠C=∠D=90°,可使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是 .
5.如图所示,已知在△ABC中,∠C=90°,AE=AC,DE⊥AB 交AB于点E,若∠B=40°,则∠ADE= .
6.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
7.如图,AD是△ABC的高,AD=BD=8,E是AD上的一点,BE=AC,AE=2,BE的延长线交AC于点F,则CD的长为 .
8.如图,已知Rt△ABC中.∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
9.如图,∠A=∠B=90°,E 是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形 并说明理由.
参考答案
夯基础
1.B 2.C 3.D 4.7
5.证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°,
∵D为AC的中点,∴AD=CD,
在Rt△ADE和Rt△CDF中, ∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,∴BA=BC,
∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.
练能力
1.D 2.A 3.C 4.(示例)AC=AD 5.65° 6.12 7.6
8.解:猜想:BF⊥AE.
理由:∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD= ∠CAE.
又∵∠CAE+∠E=90°.∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
9.解:(1)证明:∵∠1=∠2,∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,∴∠DEC=180°-90°=90°,
∴△DEC为直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
3 直角三角形
第2课时 “HL”定理
夯基础
1.下列条件中,不能判定两个直角三角形全等的是 ( )
A.两条直角边对应相等 B.两个锐角对应相等
C.一个锐角和一条直角边对应相等 D.斜边和一条直角边对应相等
2.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6cm,则AE+DE 等于 ( )
A.4cm B.5cm C.6 cm D.7cm
3.如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A.(5,4) B.(3,4) C.(5,3) D.(4,3)
4.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C在直线PQ上,点E在AB 上,AD+BC=7,AD=EB,DE=EC,则AB= .
5.如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为E,F,且DE=DF.求证:△ABC是等边三角形.
练能力
1.如图,已知点A,D,C,F在同一条直线上,∠B=∠E=90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是 ( )
A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF
2.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
3.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
4.如图所示,∠C=∠D=90°,可使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是 .
5.如图所示,已知在△ABC中,∠C=90°,AE=AC,DE⊥AB 交AB于点E,若∠B=40°,则∠ADE= .
6.如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
7.如图,AD是△ABC的高,AD=BD=8,E是AD上的一点,BE=AC,AE=2,BE的延长线交AC于点F,则CD的长为 .
8.如图,已知Rt△ABC中.∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.
9.如图,∠A=∠B=90°,E 是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形 并说明理由.
参考答案
夯基础
1.B 2.C 3.D 4.7
5.证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°,
∵D为AC的中点,∴AD=CD,
在Rt△ADE和Rt△CDF中, ∴Rt△ADE≌Rt△CDF(HL),
∴∠A=∠C,∴BA=BC,
∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.
练能力
1.D 2.A 3.C 4.(示例)AC=AD 5.65° 6.12 7.6
8.解:猜想:BF⊥AE.
理由:∵∠ACB=90°,∴∠ACE=∠BCD=90°.
又∵BC=AC,BD=AE,∴Rt△BDC≌Rt△AEC(HL).
∴∠CBD= ∠CAE.
又∵∠CAE+∠E=90°.∴∠EBF+∠E=90°.
∴∠BFE=90°,即BF⊥AE.
9.解:(1)证明:∵∠1=∠2,∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
∴Rt△ADE≌Rt△BEC(HL);
(2)△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,∴∠DEC=180°-90°=90°,
∴△DEC为直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
