3.7切线长定理 学案
图片预览



文档简介
中小学教育资源及组卷应用平台
3.7切线长定理 导学案
课题 3.7切线长定理 单元 第3单元 学科 数学 年级 九年级(下)
教材分析 理解切线长的概念,掌握切线长定理.利用切线长定理进行有关的计算;并在运用切线长定理的解题过程中,进一步渗透方程的思想.
核心素养分析 通过经历探索切线长定理的过程,发展探究意识和体会并实践“实验几何——论证几何”的探究方法,通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力.
学习目标 1、理解切线长的概念和定理,学会判定圆的切线,并且求出切线的长;2、利用切线长定理证明与圆切线相关的几何题;3、掌握切线长定理与圆其他知识点的综合应用.
重点 切线长定理及应用.
难点 切线长定理及应用、初步学会运用切线长定理进行计算与证明.
教学过程
课前预学 引入思考探究一: 过圆外一点画圆的切线,你能画出几条?试试看.如图 3-30,PA,PB 是 ⊙O 的两条切线,A, B 是切点. 这个图形是轴对称图形吗?如果是,它的对称轴是什么? (2)在这个图中你能找到相等的线段吗?说说你的理由.过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长(length of the tangent).切线长定理 过圆外一点所画的圆的两条切线的长相等.探究二: 已知:如图 3-31,PA,PB 是 ⊙O 的两条切线,A,B 是切点. 求证:PA = PB.图 3-31
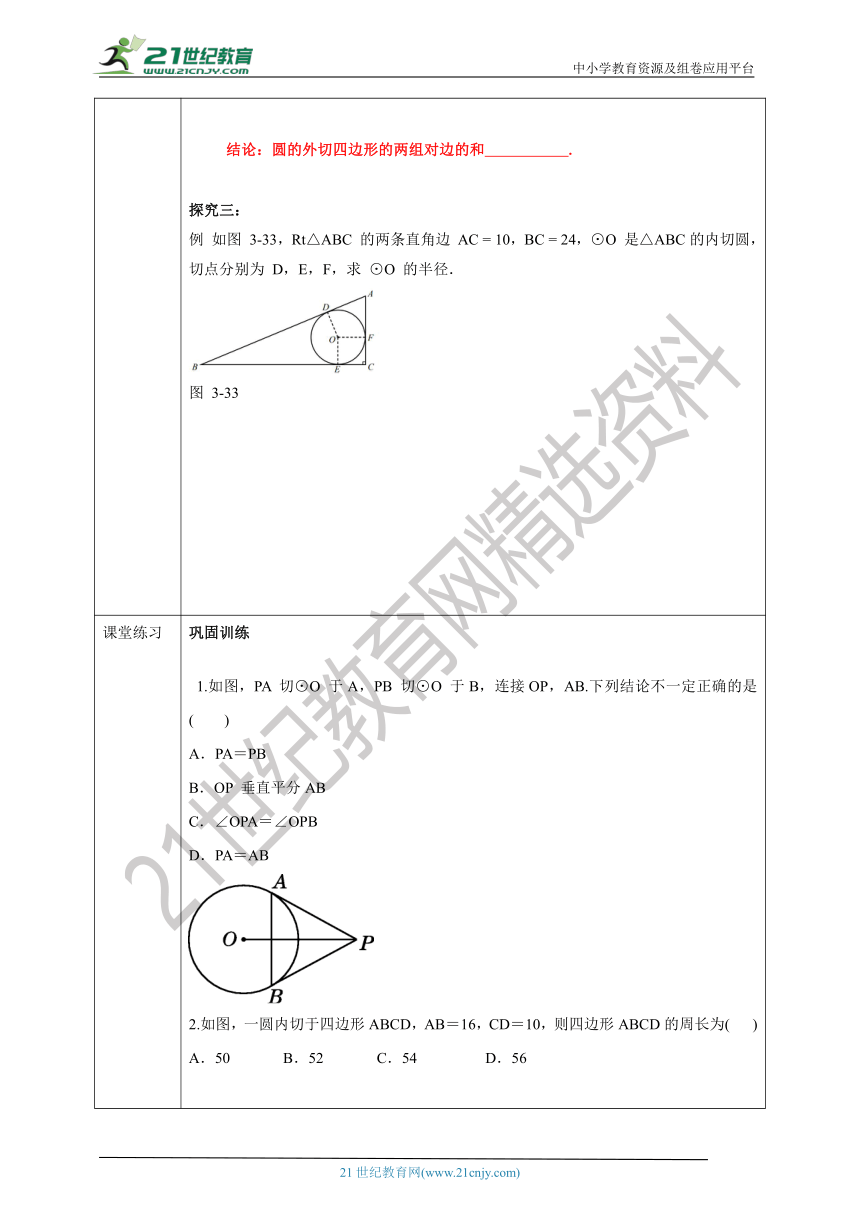
新知讲解 提炼概念切线长定理:从圆外一点所画的圆的两条切线长 .典例精讲 思考:如图 3-32,四边形 ABCD 的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.图 3-32结论:圆的外切四边形的两组对边的和 .探究三: 例 如图 3-33,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC的内切圆,切点分别为 D,E,F,求 ⊙O 的半径.图 3-33
课堂练习 巩固训练 1.如图,PA 切⊙O 于A,PB 切⊙O 于B,连接OP,AB.下列结论不一定正确的是( )A.PA=PB B.OP 垂直平分AB C.∠OPA=∠OPB D.PA=AB2.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )A.50 B.52 C.54 D.563.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= . 4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .5.如图,○O是三角形纸片ABC的内切圆,在○O的右侧沿着○O相切的直线MN剪下△AMN.若△ABC的周长为15cm,BC=4cm,则剪下的△AMN的周长为多少cm?6.△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长. 7.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.答案引入思考探究二:证明:连接OA,OB;∵PA,PB是⊙O的两条切线, ∴ ∠PAO=∠PBO=90.在Rt△PAO和Rt△PBO中 ,∵OA=OB,OP=OP,∴ Rt△PAO≌ Rt△PBO.∴PA=PB.提炼概念典例精讲 例:巩固训练D2. B3. 65 °或115 °4. 245. 解:∵○O是三角形纸片ABC的内切圆,MN与○O相切,∴BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,即剪下的△AMN的周长为7cm,故答案为:7.6.7.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
3.7切线长定理 导学案
课题 3.7切线长定理 单元 第3单元 学科 数学 年级 九年级(下)
教材分析 理解切线长的概念,掌握切线长定理.利用切线长定理进行有关的计算;并在运用切线长定理的解题过程中,进一步渗透方程的思想.
核心素养分析 通过经历探索切线长定理的过程,发展探究意识和体会并实践“实验几何——论证几何”的探究方法,通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力.
学习目标 1、理解切线长的概念和定理,学会判定圆的切线,并且求出切线的长;2、利用切线长定理证明与圆切线相关的几何题;3、掌握切线长定理与圆其他知识点的综合应用.
重点 切线长定理及应用.
难点 切线长定理及应用、初步学会运用切线长定理进行计算与证明.
教学过程
课前预学 引入思考探究一: 过圆外一点画圆的切线,你能画出几条?试试看.如图 3-30,PA,PB 是 ⊙O 的两条切线,A, B 是切点. 这个图形是轴对称图形吗?如果是,它的对称轴是什么? (2)在这个图中你能找到相等的线段吗?说说你的理由.过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长(length of the tangent).切线长定理 过圆外一点所画的圆的两条切线的长相等.探究二: 已知:如图 3-31,PA,PB 是 ⊙O 的两条切线,A,B 是切点. 求证:PA = PB.图 3-31
新知讲解 提炼概念切线长定理:从圆外一点所画的圆的两条切线长 .典例精讲 思考:如图 3-32,四边形 ABCD 的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.图 3-32结论:圆的外切四边形的两组对边的和 .探究三: 例 如图 3-33,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC的内切圆,切点分别为 D,E,F,求 ⊙O 的半径.图 3-33
课堂练习 巩固训练 1.如图,PA 切⊙O 于A,PB 切⊙O 于B,连接OP,AB.下列结论不一定正确的是( )A.PA=PB B.OP 垂直平分AB C.∠OPA=∠OPB D.PA=AB2.如图,一圆内切于四边形ABCD,AB=16,CD=10,则四边形ABCD的周长为( )A.50 B.52 C.54 D.563.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点C是⊙O上异于A、B的点,则∠ACB= . 4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3, BD+CE=12, 则△ABC的周长是 .5.如图,○O是三角形纸片ABC的内切圆,在○O的右侧沿着○O相切的直线MN剪下△AMN.若△ABC的周长为15cm,BC=4cm,则剪下的△AMN的周长为多少cm?6.△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长. 7.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.答案引入思考探究二:证明:连接OA,OB;∵PA,PB是⊙O的两条切线, ∴ ∠PAO=∠PBO=90.在Rt△PAO和Rt△PBO中 ,∵OA=OB,OP=OP,∴ Rt△PAO≌ Rt△PBO.∴PA=PB.提炼概念典例精讲 例:巩固训练D2. B3. 65 °或115 °4. 245. 解:∵○O是三角形纸片ABC的内切圆,MN与○O相切,∴BC+BD+CE=2BC=8,MN+MA+AN=AD+AE=15-8=7,即剪下的△AMN的周长为7cm,故答案为:7.6.7.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
