10.5 角平分线同步练习（含答案）

中小学教育资源及组卷应用平台
第十章 三角形的有关证明
5 角平分线
夯基础
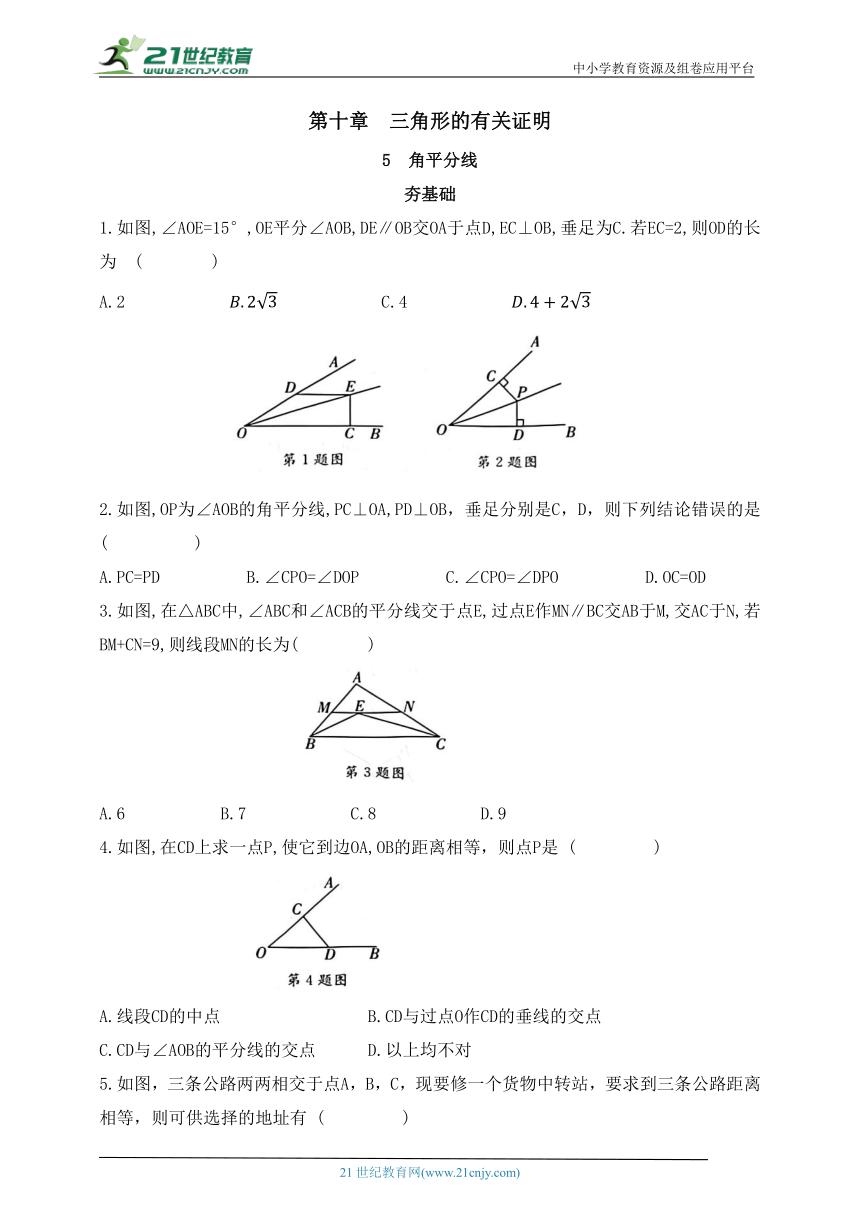
1.如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为 ( )
A.2 C.4
2.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB，垂足分别是C，D，则下列结论错误的是 ( )
A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
A.6 B.7 C.8 D.9
4.如图,在CD上求一点P,使它到边OA,OB的距离相等，则点P是 ( )
A.线段CD的中点 B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点 D.以上均不对
5.如图，三条公路两两相交于点A，B，C，现要修一个货物中转站，要求到三条公路距离相等，则可供选择的地址有 ( )
A.一处 B.两处 C.三处 D.四处
6.如图,在△ABC中,根据尺规作图痕迹，下列说法不一定正确的是 ( )
A.AF=BF C.∠DBF+∠DFB=90° D.∠BAF=∠EBC
练能力
1.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为 ( )
A.8 B.7.5 C.15 D.无法确定
2.如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点D，DE是AB的垂直平分线，垂足为E.若BC=3,则DE的长为 ( )
A.1 B.2 C.3 D.5
3.如图,在△ABC中,若∠BAC=80°,∠ACB=70°,根据图中尺规作图的痕迹推断，以下结论错误的是 ( )
A.∠BAQ=40° C.AF=AC D.∠EQF=25°
4.如图,在Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD；分别以D，E为圆心、以大于的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G.若CG=1,P为AB上一动点，则GP的最小值为( )
A.无法确定 C.1 D.2
5.如图,AB∥CD,BP和CP 分别平分∠ABC和∠BCD,AD过点P且与AB垂直,若AD=8,BC=10,则△BCP的面积为( )
A.16 B.20 C.40 D.80
6.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP= ( )
A.40° B.45° C.50° D.60°
7.如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上.若AB=3,BC=4,则BD= .
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则
9.如图，点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是射线OC上一动点,则PM的最小值为 .
10.如图,在△ABC中,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,若△ABC的周长是20,且△ABC的面积为60,则OD= .
11.如图,在△ABC中,∠C=90°,AC=BC.以点A为圆心,以任意长为半径作弧交AB，AC于D，E两点；分别以点D，E为圆心，以大于 长为半径作弧，在∠BAC内两弧相交于点P；作射线AP交BC于点F,过点F作FG⊥AB,垂足为G.若AB=8cm,则△BFG的周长等于 cm.
12.如图,点C,D在∠AOB的平分线上,DM⊥AC 于点M,DN⊥BC于点N,DM=DN.求证:OA=OB.
13.在公路同侧，异侧的两个城镇A，B，如图.电信部门要修建一座信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条公路的距离也必须相等，发射塔C应建在什么位置 请用尺规作图找出所有符合条件的点，注明点C的位置.(保留作图痕迹，不要求写出画法)
14.已知:Rt△ABC,∠B=90°.
求作:点P,使点P在△ABC内部,且PB=PC,∠PBC=45°.
参考答案
夯基础
1.C 2.B 3.D 4.C 5.D 6.B
练能力
1.B 2.A 3.D 4.C 5.B
6.C 解析:延长BA,BC,作PN⊥BC,PF⊥BA,PM ⊥AC,垂足分别为N,F,M.
设∠PCD=x°.
∵CP平分∠ACD, ∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,∴∠ABP=∠PBC=∠PCD-∠BPC=( x-40)°,
∴∠BAC=∠ACD-∠ABC=2x°-(x°-40°)-(x°-40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中, ∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.故选:C.
8.1 9.3 10.6 11.8
12.证明:∵DM⊥AC,DN⊥BC,DM=DN,∴CD是∠ACB的角平分线,
∴∠ACD=∠BCD,∴180°-∠ACD=180°-∠BCD,
即∠ACO=∠BCO,
∵点C,D在∠AOB的平分线上,∴∠AOC=∠BOC,
又∵OC=OC,∴△AOC≌△BOC(ASA),∴OA=OB.
13.解：作两条公路夹角的平分线OD，OE；作线段AB的垂直平分线FG；则射线OD，OE 与直线FG的交点C ，C 就是所求的位置.
14.解：如图，点P即为所求：
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)