第十章 三角形的有关证明章末复习题(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明章末复习题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十章 三角形的有关证明
章末复习
考点① 全等三角形
考查1 全等三角形的性质
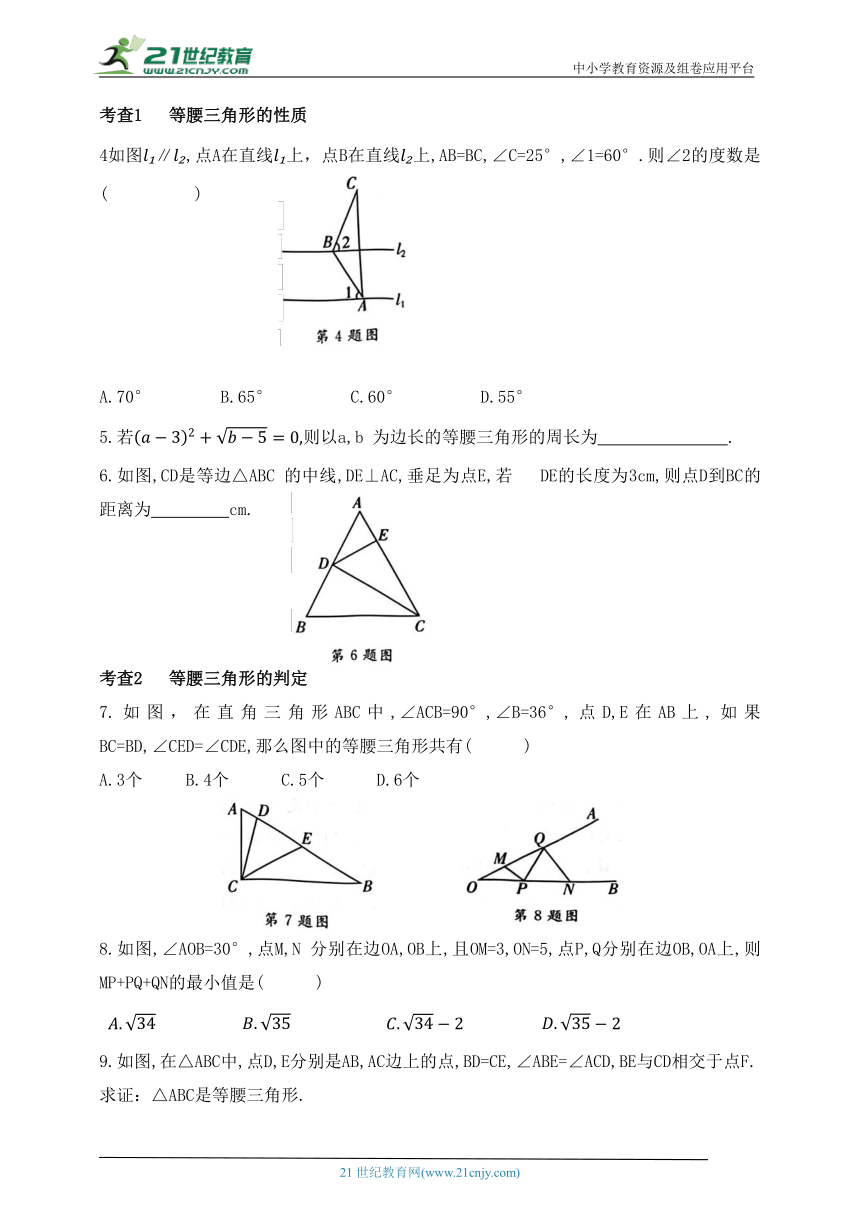
1.如图所示,△ABC ≌△AEF,在下列结论中,不正确的是 ( )
A.∠EAB=∠FAC B.BC=EF C.∠BAC=∠CAF D.CA平分∠BCF
考查2 全等三角形的判定
2.如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件 , 使Rt△ABC和Rt△EDF全等.
3.如图,B是线段AC的中点,AD∥BE,BD∥CE,求证:△ABD≌△BCE.
考点② 等腰三角形
考查1 等腰三角形的性质
4如图∥,点A在直线上,点B在直线上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是 ( )
A.70° B.65° C.60° D.55°
5.若则以a,b 为边长的等腰三角形的周长为 .
6.如图,CD是等边△ABC 的中线,DE⊥AC,垂足为点E,若 DE的长度为3cm,则点D到BC的距离为 cm.
考查2 等腰三角形的判定
7.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D,E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )
A.3个 B.4个 C.5个 D.6个
8.如图,∠AOB=30°,点M,N 分别在边OA,OB上,且OM=3,ON=5,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是( )
9.如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.
求证:△ABC是等腰三角形.
考点③ 直角三角形
考查1 勾股定理
10.直角三角形两边长为5和12,则第三边长为 .
11.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,弦隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25; ,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17; 若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 .(结果用含m的式子表示)
考查2 勾股定理的逆定理
12.下列各数,能构成直角三角形的是( )
A.0.3,0.4 ,0.5
考查3 含30°角的直角三角形的性质
13.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是 ( )
A.3 m B.4 m C.5 m D.6 m
14.如图,在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,AB=10,求BD的长.
考点④ 互逆命题
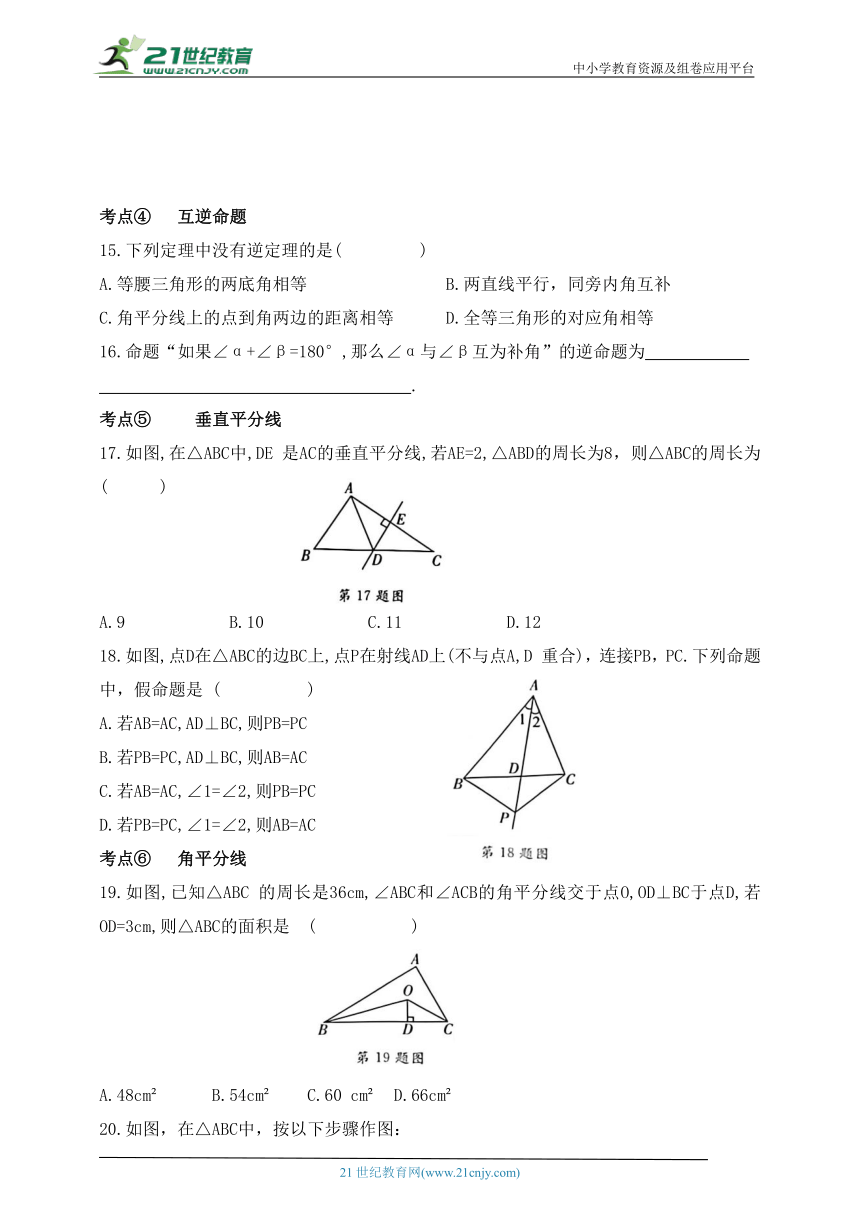
15.下列定理中没有逆定理的是( )
A.等腰三角形的两底角相等 B.两直线平行,同旁内角互补
C.角平分线上的点到角两边的距离相等 D.全等三角形的对应角相等
16.命题“如果∠α+∠β=180°,那么∠α与∠β互为补角”的逆命题为____________
____________________________________.
考点⑤ 垂直平分线
17.如图,在△ABC中,DE 是AC的垂直平分线,若AE=2,△ABD的周长为8,则△ABC的周长为 ( )
A.9 B.10 C.11 D.12
18.如图,点D在△ABC的边BC上,点P在射线AD上(不与点A,D 重合),连接PB,PC.下列命题中,假命题是 ( )
A.若AB=AC,AD⊥BC,则PB=PC
B.若PB=PC,AD⊥BC,则AB=AC
C.若AB=AC,∠1=∠2,则PB=PC
D.若PB=PC,∠1=∠2,则AB=AC
考点⑥ 角平分线
19.如图,已知△ABC 的周长是36cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是 ( )
A.48cm B.54cm C.60 cm D.66cm
20.如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交AB,BC于点D,E.
②分别以点D,E为圆心,大于的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果AB=8,BC=12,△ABG的面积为18,则△CBG的面积为 .21.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点O,OB=OC.求证:∠1=∠2.
考点⑦ 尺规作图
22.用尺规作一个角的角平分线,下列作法中错误的是( )
23.如图,在△ABC中,点P是AC 上一点,连接BP,求作一点M,使得点M 到AB和AC两边的距离相等,并且到点B 和点P的距离相等.(不写作法,保留作图痕迹)
参考答案
1.C 2.(示例)AB=ED
3.证明:∵B是AC中点,∴AB=BC,
∵AD∥BE,∴∠A=∠EBC,
∵BD∥EC,∴∠DBA=∠C,
在△ABD和△BCE中,
∴△ABD≌△BCE(ASA).
4.A 5.11或13 6.3 7.B
8.A 解析:作M关于OB的对称点作N关于OA的对称点如图所示.
连接M'N',即为MP+PQ+QN的最小值.
根据轴对称的定义可知
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴在中,
故选:A.
9.证明:∵∠ABE=∠ACD,∴∠DBF=∠ECF.
在△BDF和△CEF中, ∴△BDF≌△CEF(AAS).
∴BF=CF,DF=EF.∴BF+EF=CF+DF.即BE=CD.
在△ABE和△ACD中, ∴△ABE≌△ACD(AAS).
∴AB=AC.∴△ABC是等腰三角形.
10.13或
11.m +1 解析:∵m为正整数,∴2m为偶数,设其股是a,则弦为a+2,
根据勾股定理,得 (2m) +a =(a+2) ,解得a=m -1,
∴弦是a+2=m -1+2=m +1.
故答案为: m +1.
12.A 13.B
14.解:在△ABC中,
∵∠A:∠B:∠C=1:2:3,∴设∠A=β,∠B=2β,∠C=3β.
由内角和定理,得∠A+∠B+∠C=180°,∴∠A=30°,∠B=60°.
∵CD ⊥AB,∴∠BDC=90°,
在Rt△BCD中,∠B=60°,∴∠BCD=90°-60°=30°.
15.D
16.如果∠α与∠β互为补角,那么∠α+∠β=180°
17.D
18.D 解析:∵AB=AC,且AD⊥BC,得AP是BC的垂直平分线,∴PB=PC,则A是真命题;
∵PB=PC,且AD⊥BC,得AP是BC的垂直平分线,∴AB=AC,则B是真命题;
∵AB=AC,且∠1=∠2,得AP是BC的垂直平分线,∴PB=PC,则C是真命题;
∵PB=PC,△BCP是等腰三角形,∠1=∠2,不能判断AP是BC的垂直平分线,
∴AB 和AC不一定相等,则D是假命题.
故选:D.
19.B 20.27
21.证明:∵CD⊥AB于D点,BE⊥AC于点E,
∴∠BDO=∠CEO=90°,
在△BDO和△CEO中, △BDO≌△CEO(AAS),
∴OD=OE,
∵OD⊥AB,OE⊥AC,∴OA平分∠BAC,∴∠1=∠2.
22.D
23.解:如图所示,点M即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十章 三角形的有关证明
章末复习
考点① 全等三角形
考查1 全等三角形的性质
1.如图所示,△ABC ≌△AEF,在下列结论中,不正确的是 ( )
A.∠EAB=∠FAC B.BC=EF C.∠BAC=∠CAF D.CA平分∠BCF
考查2 全等三角形的判定
2.如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件 , 使Rt△ABC和Rt△EDF全等.
3.如图,B是线段AC的中点,AD∥BE,BD∥CE,求证:△ABD≌△BCE.
考点② 等腰三角形
考查1 等腰三角形的性质
4如图∥,点A在直线上,点B在直线上,AB=BC,∠C=25°,∠1=60°.则∠2的度数是 ( )
A.70° B.65° C.60° D.55°
5.若则以a,b 为边长的等腰三角形的周长为 .
6.如图,CD是等边△ABC 的中线,DE⊥AC,垂足为点E,若 DE的长度为3cm,则点D到BC的距离为 cm.
考查2 等腰三角形的判定
7.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D,E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )
A.3个 B.4个 C.5个 D.6个
8.如图,∠AOB=30°,点M,N 分别在边OA,OB上,且OM=3,ON=5,点P,Q分别在边OB,OA上,则MP+PQ+QN的最小值是( )
9.如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.
求证:△ABC是等腰三角形.
考点③ 直角三角形
考查1 勾股定理
10.直角三角形两边长为5和12,则第三边长为 .
11.勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,弦隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25; ,这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17; 若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 .(结果用含m的式子表示)
考查2 勾股定理的逆定理
12.下列各数,能构成直角三角形的是( )
A.0.3,0.4 ,0.5
考查3 含30°角的直角三角形的性质
13.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是 ( )
A.3 m B.4 m C.5 m D.6 m
14.如图,在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,AB=10,求BD的长.
考点④ 互逆命题
15.下列定理中没有逆定理的是( )
A.等腰三角形的两底角相等 B.两直线平行,同旁内角互补
C.角平分线上的点到角两边的距离相等 D.全等三角形的对应角相等
16.命题“如果∠α+∠β=180°,那么∠α与∠β互为补角”的逆命题为____________
____________________________________.
考点⑤ 垂直平分线
17.如图,在△ABC中,DE 是AC的垂直平分线,若AE=2,△ABD的周长为8,则△ABC的周长为 ( )
A.9 B.10 C.11 D.12
18.如图,点D在△ABC的边BC上,点P在射线AD上(不与点A,D 重合),连接PB,PC.下列命题中,假命题是 ( )
A.若AB=AC,AD⊥BC,则PB=PC
B.若PB=PC,AD⊥BC,则AB=AC
C.若AB=AC,∠1=∠2,则PB=PC
D.若PB=PC,∠1=∠2,则AB=AC
考点⑥ 角平分线
19.如图,已知△ABC 的周长是36cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是 ( )
A.48cm B.54cm C.60 cm D.66cm
20.如图,在△ABC中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交AB,BC于点D,E.
②分别以点D,E为圆心,大于的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果AB=8,BC=12,△ABG的面积为18,则△CBG的面积为 .21.如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD交于点O,OB=OC.求证:∠1=∠2.
考点⑦ 尺规作图
22.用尺规作一个角的角平分线,下列作法中错误的是( )
23.如图,在△ABC中,点P是AC 上一点,连接BP,求作一点M,使得点M 到AB和AC两边的距离相等,并且到点B 和点P的距离相等.(不写作法,保留作图痕迹)
参考答案
1.C 2.(示例)AB=ED
3.证明:∵B是AC中点,∴AB=BC,
∵AD∥BE,∴∠A=∠EBC,
∵BD∥EC,∴∠DBA=∠C,
在△ABD和△BCE中,
∴△ABD≌△BCE(ASA).
4.A 5.11或13 6.3 7.B
8.A 解析:作M关于OB的对称点作N关于OA的对称点如图所示.
连接M'N',即为MP+PQ+QN的最小值.
根据轴对称的定义可知
∴△ONN′为等边三角形,△OMM′为等边三角形,
∴在中,
故选:A.
9.证明:∵∠ABE=∠ACD,∴∠DBF=∠ECF.
在△BDF和△CEF中, ∴△BDF≌△CEF(AAS).
∴BF=CF,DF=EF.∴BF+EF=CF+DF.即BE=CD.
在△ABE和△ACD中, ∴△ABE≌△ACD(AAS).
∴AB=AC.∴△ABC是等腰三角形.
10.13或
11.m +1 解析:∵m为正整数,∴2m为偶数,设其股是a,则弦为a+2,
根据勾股定理,得 (2m) +a =(a+2) ,解得a=m -1,
∴弦是a+2=m -1+2=m +1.
故答案为: m +1.
12.A 13.B
14.解:在△ABC中,
∵∠A:∠B:∠C=1:2:3,∴设∠A=β,∠B=2β,∠C=3β.
由内角和定理,得∠A+∠B+∠C=180°,∴∠A=30°,∠B=60°.
∵CD ⊥AB,∴∠BDC=90°,
在Rt△BCD中,∠B=60°,∴∠BCD=90°-60°=30°.
15.D
16.如果∠α与∠β互为补角,那么∠α+∠β=180°
17.D
18.D 解析:∵AB=AC,且AD⊥BC,得AP是BC的垂直平分线,∴PB=PC,则A是真命题;
∵PB=PC,且AD⊥BC,得AP是BC的垂直平分线,∴AB=AC,则B是真命题;
∵AB=AC,且∠1=∠2,得AP是BC的垂直平分线,∴PB=PC,则C是真命题;
∵PB=PC,△BCP是等腰三角形,∠1=∠2,不能判断AP是BC的垂直平分线,
∴AB 和AC不一定相等,则D是假命题.
故选:D.
19.B 20.27
21.证明:∵CD⊥AB于D点,BE⊥AC于点E,
∴∠BDO=∠CEO=90°,
在△BDO和△CEO中, △BDO≌△CEO(AAS),
∴OD=OE,
∵OD⊥AB,OE⊥AC,∴OA平分∠BAC,∴∠1=∠2.
22.D
23.解:如图所示,点M即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
