沪科版数学七下6.2《实数》(第1课时)课件
文档属性
| 名称 | 沪科版数学七下6.2《实数》(第1课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 178.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-27 00:00:00 | ||
图片预览






文档简介
课件16张PPT。6.2 实数(一)
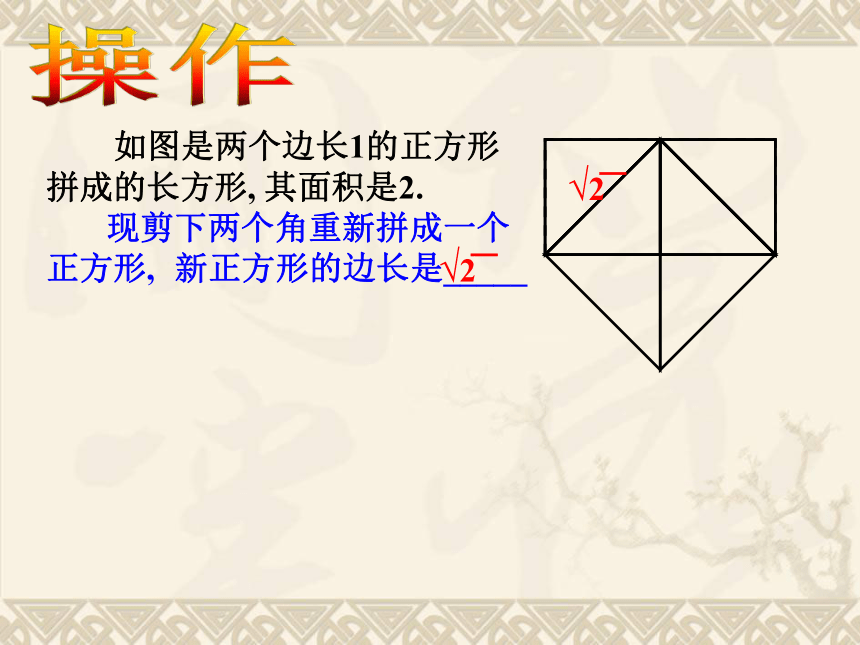
如图是两个边长1的正方形操作拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 是不是有理数?是不是整数?是不是分数?结论: 既不是整数,也不是分数。
所以, 不是有理数。议一议 用这种方法可以得到一系列越来越接近 的 近似值。 我们把这种无限不循环小数叫做无理数。圆周率 及一些含有 的数都是无理数例如:2)像 的数是无理数。1) 3) 有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
想一想:凡是带有根号的数都是无理数吗?判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:, , , ,超级演练
有理数集合 无理数集合 正数集合 负数集合实数可以分为正实数、0、负实数有理数和无理数统称实数。 实数有理数无理数正有理数零负有理数正无理数负无理数有限小数或
无限循环小数无限不循环小数 例1:把下列各数填入相应的集合里 , , 0.353353335…, , , ,cos60°, 0, tan45°, ,
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π0.353353335… , tan45°, ,0, ,π, cos60°,例2:最小的正整数与最大的负整数之和是_____.0练一练1.把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:ooo2.把下列各数分别填入相应的集合内:(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合1、判断下列说法是否正确:1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
7.平面直角坐标系中的点与有序实数对之间是
一一对应的。( ) √整数有
有理数有
无理数有
实数有二、填空6、在实数
中,
如图是两个边长1的正方形操作拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 是不是有理数?是不是整数?是不是分数?结论: 既不是整数,也不是分数。
所以, 不是有理数。议一议 用这种方法可以得到一系列越来越接近 的 近似值。 我们把这种无限不循环小数叫做无理数。圆周率 及一些含有 的数都是无理数例如:2)像 的数是无理数。1) 3) 有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
—234.232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
想一想:凡是带有根号的数都是无理数吗?判断下列数哪些是有理数?哪些是无理数? 有理数是:
无理数是:, , , ,超级演练
有理数集合 无理数集合 正数集合 负数集合实数可以分为正实数、0、负实数有理数和无理数统称实数。 实数有理数无理数正有理数零负有理数正无理数负无理数有限小数或
无限循环小数无限不循环小数 例1:把下列各数填入相应的集合里 , , 0.353353335…, , , ,cos60°, 0, tan45°, ,
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π0.353353335… , tan45°, ,0, ,π, cos60°,例2:最小的正整数与最大的负整数之和是_____.0练一练1.把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:ooo2.把下列各数分别填入相应的集合内:(相邻两个3之间的7的个数逐次加1) 有理数集合 无理数集合1、判断下列说法是否正确:1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
7.平面直角坐标系中的点与有序实数对之间是
一一对应的。( ) √整数有
有理数有
无理数有
实数有二、填空6、在实数
中,
