第一单元 扇形统计图( 知识通关练)-2022-2023学年六年级数学下册单元测试卷(苏教版) (2)(含解析)
文档属性
| 名称 | 第一单元 扇形统计图( 知识通关练)-2022-2023学年六年级数学下册单元测试卷(苏教版) (2)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 00:00:00 | ||
图片预览




文档简介
2022-2023学年六年级数学下册单元测试卷(苏教版)
第一单元 扇形统计图( 知识通关练)
考试时间:60分钟;试卷满分:100分
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共16分,每小题2分)
1.从下面两个统计图中可以看出,甲班男生人数与乙班男生人数比较,( )。
A.甲班男生人数多 B.乙班男生人数多 C.无法确定
2.2020年上半年兴义市生产总值为204.08亿元,如果想要表示劳动报酬、生产税净额、营业盈余等与生产总值的关系,选择( )更合适。
A.条形统计图 B.扇形统计图
C.折线统计图 D.统计表
3.下列信息中,最适合用扇形统计图表示的是( )。
A.小明6~12岁的身高变化 B.牛奶的营养成分
C.小红5次数学检测的成绩 D.某班男生的体重
4.如图是“百姓热线电话”一周内接到的热线电话情况统计图,其中关于环境保护问题的电话70个,本周“百姓热线电话”共接热线电话( )个。
A.180 B.190 C.200
5.育新小学六年级学生喜欢的运动项目统计如图所示,其中喜欢足球的有40人。下列说法正确的是( )。
A.喜欢踢毽子的人数最少
B.喜欢跳绳的有 30人
C.喜欢乒乓球的人数最多
6.下面各信息中,最适合用扇形统计图表示的是( )。
A.某校各学科教师人数占全校教师的百分比情况
B.小明家5年内旅游消费增减变化情况
C.华为手机和苹果手机2018年每月销售情况
D.5月份气温变化情况
7.条形统计图纵轴如果用2格表示20人,那么要表示120人需要画( )格。
A.6 B.7 C.12 D.13
8.六(1)班美术兴趣小组的人数是全班人数的27.1%,下面是制作统计图是画的4个草图,其中图( )能比较正确地表示这个百分比。
A. B. C. D.
二、填空题(共16分,每小题2分)
9.常见的统计图有( )统计图、( )统计图、( )统计图,为反映各部分在总体中所占的百分比,一般选择( )统计图。
10.扇形统计图用整个( )表示总数,用圆内各个( )的大小表示各部分在总体中所占的百分比,通过扇形统计图可以很清楚地表示出( )与( )之间的关系。
11.扇形统计图可以直观、清楚地表示出( )占总体的百分之多少。
12.在一所民族小学里,为了表示出各民族学生人数占总人数的百分比情况,可以选用________统计图。
13.鸡蛋中各部分质量统计图如图。丽丽每天早晨都吃一个鸡蛋(一个鸡蛋大约重0.06千克),丽丽每天摄入的蛋白有( )克,蛋黄有( )克。
14.条形统计图的特点是( ),扇形统计图的特点是( )。
15.“接种新冠疫苗,共筑免疫长城”,如果要反映每日接种疫苗人数增减变化情况,应选用( )统计图,如果要反映各省接种疫苗人数与全国接种疫苗人数之间的关系,应选用( )统计图。
16.要更清楚地看出各部分与整体之间的关系,用( )统计图表示最合适。
三、判断题(共8分,每小题2分)
17.扇形统计图最大的优点是能表示各部分数量与总数的关系。( )
18.某同学为了统计自己家一天消费的各类食物所占百分比情况,他应选用扇形统计图比较合适.( )
19.要表示某种矿泉水中各种矿物质的含量占总量的多少,选用折线统计图比较合适。( )
20.扇形统计图中,所有扇形的百分比之和必须小于1。( )
四、作图题(共6分)
21.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
五、解答题(共54分,每小题9分)
22.观察下图,解决问题。
(1)这是( )统计图。
(2)B部分占整体的( )%,图中A、B、C三部分的最简比是( )。
(3)如果这是育才小学六年级学生视力情况统计图。其中A表示正常人数, B表示近视人数,C表示假性近视人数。六年级共有400人,假性近视有多少人?
23.如图是笑笑家12月总支出情况统计图。
(1)从这个扇形统计图可以看出:文化支出占总支出的( )%,几项支出中,占比最大的支出是( )。
(2)如果生活支出比文化支出多260元,那么笑笑家12月总支出是多少元?(写出解题过程)
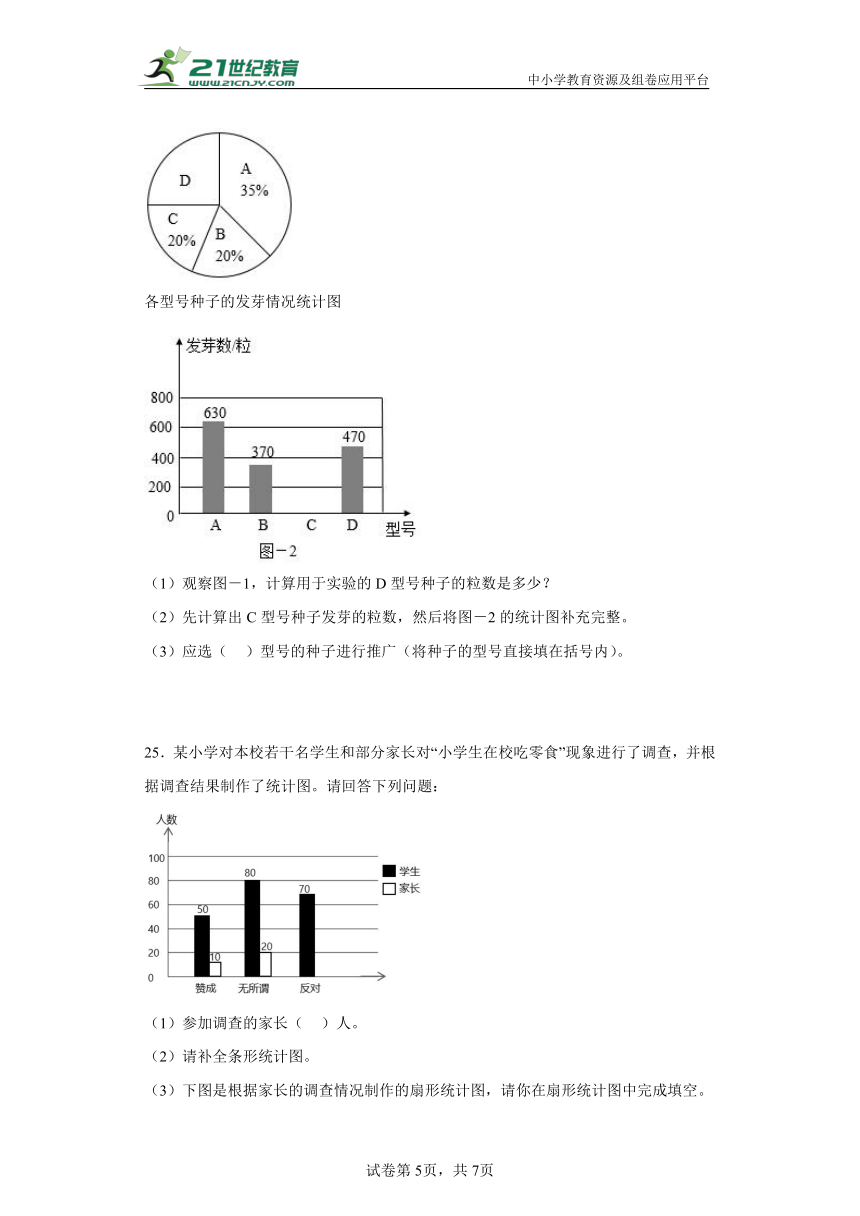
24.某种子培育基地用A、B、C、D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广。通过实验得知,C型号种子的发芽率为95%。以下是根据实验数据绘制的图-1和图-2两幅尚不完整的统计图。
用于实验的各型号种子数的百分比
各型号种子的发芽情况统计图
(1)观察图-1,计算用于实验的D型号种子的粒数是多少?
(2)先计算出C型号种子发芽的粒数,然后将图-2的统计图补充完整。
(3)应选( )型号的种子进行推广(将种子的型号直接填在括号内)。
25.某小学对本校若干名学生和部分家长对“小学生在校吃零食”现象进行了调查,并根据调查结果制作了统计图。请回答下列问题:
(1)参加调查的家长( )人。
(2)请补全条形统计图。
(3)下图是根据家长的调查情况制作的扇形统计图,请你在扇形统计图中完成填空。
(4)从这次接受调查的家长中任意抽查一名家长,抽到持哪类态度的可能性大?
26.小华家去年支出情况如图所示,若小华家去年衣食住行用去4.5万元.那么他家去年存入银行的钱有多少万元?
27.下图是根据六年级1班一次数学测试成绩数据绘制成的统计图,请结合两幅统计图提供的信息,回答下面问题。
(1)优秀人数比及格人数多__________;
(2)六年级1班有__________人参加本次数学测试;
(3)本次测试的优秀率是__________,不及格占本测试人数的__________;
(4)把条形统计图和扇形统计图补充或填写完整。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】题干未明确说明甲班和乙班人数相同,可知它们的单位“1”不一定相同,即可得出答案。
【详解】因为单位“1”不一定相同,所以无法比较两个班男生人数的多少。
故答案为:C。
【点睛】根据扇形统计图,考察学生对单位“1”的理解。
2.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】2020年上半年兴义市生产总值为204.08亿元,如果想要表示劳动报酬、生产税净额、营业盈余等与生产总值的关系,选择扇形统计图更合适。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况解答即可。
【详解】A.小明6~12岁的身高变化最适合用折线统计图表示。
B.牛奶的营养成分最适合用扇形统计图表示。
C.小红5次数学检测的成绩最适合用条形统计图表示。
D.某班男生的体重最适合用条形统计图表示。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
4.C
【详解】由统计图知,环境保护问题的电话占本周内接到的热线电话量的35%,根据求一个数的百分之几是多少,把本周内接到的热线电话量看作单位“1”,求单位“1”用除法计算。
70÷35%=200(个)
故答案为:C
【点睛】考查了有关扇形统计图的知识,分析图中的数据,找出相关的量进行解答。
5.B
【解析】以一个圆的面积表示育新小学六年级学生喜欢的运动项目的情况,以扇形面积表示各种运动占的百分比。从图上能够读出各种运动所占的百分比,例如足球占的百分比为20%,我们还知道喜欢足球这项运动的学生有40人,两者相结合可以求出这次调查的学生总数。再结合跳绳所占的百分比:15%,能够求出喜欢跳绳的人数。
【详解】A:12.5%<15%<20%<22.5%<30%,所以喜欢踢毽子的人数所占百分比最少,但其他中的类型和占总人数的百分数都不知道,所以无法判断最少,A错;
B:用喜欢足球的人数除以它所占的百分比可得出总人数:
40÷20%=40÷0.2=200(人)
用总人数乘喜欢跳绳的百分比就得出喜欢跳绳的人数:
200×15%=200×0.15=30(人)B对;
C:12.5%<15%<20%<22.5%<30%,但其他中的类型和占总人数的百分数都不知道,所以无法判断最多;C错。
故答案为:B。
【点睛】数据统计的全过程有收集数据、整理数据、绘制图表、分析数据、得出结论五个环节。建立数据分析观念最好的办法是让学生经历统计的全过程。即让学生经历完整的收集、整理、描述、分析的统计全过程。
6.A
【分析】首先要清楚每一种统计图的特点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此求解即可。
【详解】A.各学科教师为部分,全校教师为整体,各学科教师占全校教师的百分比情况即部分与整体的关系,用扇形统计图表示最合适
B.要了解小明家5年内旅游消费增减变化情况,用折线统计图表示最合适
C.要了解华为手机和苹果手机2018年每月销售情况,用条形统计图表示最合适
D.要了解5月份气温变化情况,用折线统计图表示最合适
故答案为:A
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答,牢记它们各自的特点。
7.C
【分析】2格表示20人,那么1格表示:20÷2=10(人),因此用120除以10即可。
【详解】120÷10=12(格)
故答案为:C
【点睛】熟练掌握单式条形统计图的特点是解答此题的关键。
8.D
【分析】题目中已给出部分与总体的百分比,四个选项用阴影表示圆心角,可以结合圆周角360°计算出这部分所占圆心角的度数,再与四个选项相比较,可以得出答案。
【详解】360°×27.1%=97.56°
97.56°>90°
通过观察各扇形的圆心角发现,A、B、C三个扇形的圆心角均小于90°,
因此,只有D能正确表示这个百分比。
故答案为:D
【点睛】本题还有一种简单的做法:因为百分比27.1%>25%(),故只要观察四个选项中哪个图的阴影部分所占面积>,即可确定该选项是对的。
9. 条形 折线 扇形 扇形
【分析】条形统计图的特点:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图的特点:能清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
【详解】常见的统计图有条形统计图、折线统计图、扇形统计图,为反映各部分在总体中所占的百分比,一般选择扇形统计图。
【点睛】明确各种统计图的特点是解答本题的关键。
10. 圆 扇形 各部分 整体
【详解】由扇形统计图的特点可知:扇形统计图用整个圆表示总数,用圆内各个扇形的大小表示各部分在总体中所占的百分比,通过扇形统计图可以很清楚地表示出各部分与整体间的关系。
11.各部分
【详解】根据扇形统计图的特点,扇形统计图能反映各部分与整体的关系。因此,扇形统计图可以直观、清楚地表示出各部分占总体的百分之多少。
12.扇形
【分析】条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系。
【详解】为了表示出各民族学生占的比例,因为要表示部分与整体之间的关系,所以可以选用扇形统计图。
故答案为:扇形。
【点睛】本题考查的是扇形统计图的特征,关键审清题意看需要做出什么样的效果。
13. 31.8 19.2
【分析】把整个鸡蛋的质量看作单位“1”,其中蛋白约占53%,蛋黄约占32%,根据求一个数的百分之几是多少,用乘法解答。
【详解】0.06千克=60克
60×53%=31.8(克)
60×32%=19.2(克)
即丽丽每天摄入的蛋白有31.8克,蛋黄有19.2克。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,再根据求一个数的百分之几是多少的方法解决问题。
14. 能很容易看出数量的多少 能反映部分与整体的关系
【分析】根据统计图的特点填空即可。
【详解】条形统计图的特点是能很容易看出数量的多少,折线统计图的特点是不仅能看出数量的多少,而且能反映数量的增减变化情况,扇形统计图特点是能反映部分与整体的关系。
【点睛】此题考查了统计图的特点,需要牢记。
15. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析得:
“接种新冠疫苗,共筑免疫长城”,如果要反映每日接种疫苗人数增减变化情况,应选用折线统计图,如果要反映各省接种疫苗人数与全国接种疫苗人数之间的关系,应选用扇形统计图。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
16.扇形
【解析】略
17.√
【详解】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系,原题说法正确;
故答案为:√。
18.√
【详解】略
19.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映各部分数量与总数之间的关系;根据统计图的特点选择合适的统计图。
【详解】根据统计图的特点可知:要表示某种矿泉水中各种矿物质的含量占总量的多少,选用扇形统计图比较合适。
故答案为:×
【点睛】掌握条形统计图、折线统计图、扇形统计图的特点是解题的关键。
20.×
【详解】略
21.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
22.(1)扇形
(2)45,5∶9∶6
(3)120人
【分析】(1)通过观察发现此统计图把圆分成几个扇形,据此可解答。
(2)把整个圆看作单位“1”,用单位“1”减去其余的两部分的占比即可;根据比的基本性质化简即可。
(3)用总人数×假性近视所占的比重=假性近视的人数,据此可解答。
【详解】1)这是扇形统计图。
(2)1-25%-30%
=75%-30%
=45%
25%∶45%∶30%
=25∶45∶30
=5∶9∶6
(3)400×30%=120(人)
【点睛】本题考查扇形统计图,明确由整体求部分用乘法是解题的关键。
23.(1)20;生活支出;
(2)1000元
【分析】(1)根据扇形统计图的信息 ,确定文化支出所占的百分比,再根据百分数比较大小的方法比较各项支出所占的百分比,据此确定占比最大的支出。
(2)根据扇形统计图可知,生活支出比文化支出多(46%-20%),再根据已知一个数的百分之几是多少,求这个数用除法列式计算即可。
【详解】(1)文化支出占总支出的20%;
8%<16%<20%<46%
所以:几项支出中,占比最大的支出是生活支出。
(2)260÷(46%-20%)
=260÷26%
=1000(元)
答:笑笑家12月总支出是1000元。
【点睛】能读懂扇形统计图中的信息是解答本题的关键。
24.(1)500粒;
(2)380粒;图见详解;
(3)C
【分析】(1)求出D所占的百分比,进而求出D的种子粒数;
(2)求出C的种子粒数,进而求出发芽粒数,补充完整;
(3)分别求出A、B、D发芽率,发芽率高的进行推广;据此解答。
【详解】(1)(1-20%-20%-35%)×2000
=0.25×2000
=500(粒)
答:用于实验的D型号种子的粒数是500粒。
(2)2000×20%×95%
=400×0.95
=380(380)
补充如下:
(3)A发芽率:630÷(2000×35%)×100%
=630÷700
=90%
B发芽率:370÷(2000×20%)×100%
=370÷400
=92.5%
C发芽率:95%
D发芽率:470÷500×100%
=0.94×100%
=94%
90%<92.5%<94%<95%,所以应选C型号的种子进行推广。
【点睛】本题主要考查统计图的综合应用。
25.(1)100;
(2)见详解;
(3)见详解;
(4)反对
【分析】(1)参加调查的家长人数是20人,占调查家长人数的20%,根据分数除法的意义,用20÷20%求出参加调查家长的人数;
(2)参加调查家长的总人数-赞成的人数-无所谓的人数=反对的人数;
(3)用赞成的人数、反对的人数分别除以总人数,求出百分率即可;
(4)哪种所占百分率大,抽到那种的可能性就大。
【详解】(1)20÷20%=100(人)
(2)100-10-20=70(人)
补充统计图如下:
(3)10÷100=10%
70÷100=70%
补充统计图如下:
(4)70%>20%>10%
答:抽到反对态度的可能性大。
【点睛】本题主要考查统计图表的综合应用。
26.4.5÷45%×20%=2(万元)
答:存入银行的钱有2万元.
【详解】略
27.(1)50
(2)40
(3)30%;5
(4)见详解
【分析】(1)根据条形统计图,可以看出成绩是优秀的有12人,及格的有8人,先计算出优秀人数比及格人数多的人数,再除以及格的人数即可得解;
(2)根据及格的有8人,以及扇形统计图及格的占总测试人数的20%,可求出测试人数为8÷20%=40(人);
(3)用优秀的人数除以参加测试的人数,就是优秀率,用总人数单位“1”分别减去优秀人数,良好人数,及格人数所占的百分率,就是不及格人数占的百分率;
(4)先计算出及格人数、不及格人数占总人数的百分率,在扇形统计图上标出,进而用总人数分别乘良好和不及格人数占的百分率,再在条形统计图上标出即可。
【详解】(1)(12-8)÷8
=4÷8
=50%
答:优秀人数比及格人数多50%。
(2)测试人数:8÷20%=40(人)
答:六年级1班有40人参加本次数学测试。
(3)优秀率:12÷40×100%=30%
1-45%-20%-30%
=55%-20%-30%
=35%-30%
=5%
答:本次测试的优秀率是30%,不及格占本班测试人数的5%。
(4)40×45%=18(人)
40×5%=2(人)
【点睛】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题。
答案第1页,共2页
答案第1页,共2页
第一单元 扇形统计图( 知识通关练)
考试时间:60分钟;试卷满分:100分
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共16分,每小题2分)
1.从下面两个统计图中可以看出,甲班男生人数与乙班男生人数比较,( )。
A.甲班男生人数多 B.乙班男生人数多 C.无法确定
2.2020年上半年兴义市生产总值为204.08亿元,如果想要表示劳动报酬、生产税净额、营业盈余等与生产总值的关系,选择( )更合适。
A.条形统计图 B.扇形统计图
C.折线统计图 D.统计表
3.下列信息中,最适合用扇形统计图表示的是( )。
A.小明6~12岁的身高变化 B.牛奶的营养成分
C.小红5次数学检测的成绩 D.某班男生的体重
4.如图是“百姓热线电话”一周内接到的热线电话情况统计图,其中关于环境保护问题的电话70个,本周“百姓热线电话”共接热线电话( )个。
A.180 B.190 C.200
5.育新小学六年级学生喜欢的运动项目统计如图所示,其中喜欢足球的有40人。下列说法正确的是( )。
A.喜欢踢毽子的人数最少
B.喜欢跳绳的有 30人
C.喜欢乒乓球的人数最多
6.下面各信息中,最适合用扇形统计图表示的是( )。
A.某校各学科教师人数占全校教师的百分比情况
B.小明家5年内旅游消费增减变化情况
C.华为手机和苹果手机2018年每月销售情况
D.5月份气温变化情况
7.条形统计图纵轴如果用2格表示20人,那么要表示120人需要画( )格。
A.6 B.7 C.12 D.13
8.六(1)班美术兴趣小组的人数是全班人数的27.1%,下面是制作统计图是画的4个草图,其中图( )能比较正确地表示这个百分比。
A. B. C. D.
二、填空题(共16分,每小题2分)
9.常见的统计图有( )统计图、( )统计图、( )统计图,为反映各部分在总体中所占的百分比,一般选择( )统计图。
10.扇形统计图用整个( )表示总数,用圆内各个( )的大小表示各部分在总体中所占的百分比,通过扇形统计图可以很清楚地表示出( )与( )之间的关系。
11.扇形统计图可以直观、清楚地表示出( )占总体的百分之多少。
12.在一所民族小学里,为了表示出各民族学生人数占总人数的百分比情况,可以选用________统计图。
13.鸡蛋中各部分质量统计图如图。丽丽每天早晨都吃一个鸡蛋(一个鸡蛋大约重0.06千克),丽丽每天摄入的蛋白有( )克,蛋黄有( )克。
14.条形统计图的特点是( ),扇形统计图的特点是( )。
15.“接种新冠疫苗,共筑免疫长城”,如果要反映每日接种疫苗人数增减变化情况,应选用( )统计图,如果要反映各省接种疫苗人数与全国接种疫苗人数之间的关系,应选用( )统计图。
16.要更清楚地看出各部分与整体之间的关系,用( )统计图表示最合适。
三、判断题(共8分,每小题2分)
17.扇形统计图最大的优点是能表示各部分数量与总数的关系。( )
18.某同学为了统计自己家一天消费的各类食物所占百分比情况,他应选用扇形统计图比较合适.( )
19.要表示某种矿泉水中各种矿物质的含量占总量的多少,选用折线统计图比较合适。( )
20.扇形统计图中,所有扇形的百分比之和必须小于1。( )
四、作图题(共6分)
21.在“阳光大课间”活动中,学校的大队部开展以“我最喜欢的体育项目”为主题的调查活动。大队部将调查的结果分析整理后,正在绘制统计图。请你完成下面的条形统计图。
五、解答题(共54分,每小题9分)
22.观察下图,解决问题。
(1)这是( )统计图。
(2)B部分占整体的( )%,图中A、B、C三部分的最简比是( )。
(3)如果这是育才小学六年级学生视力情况统计图。其中A表示正常人数, B表示近视人数,C表示假性近视人数。六年级共有400人,假性近视有多少人?
23.如图是笑笑家12月总支出情况统计图。
(1)从这个扇形统计图可以看出:文化支出占总支出的( )%,几项支出中,占比最大的支出是( )。
(2)如果生活支出比文化支出多260元,那么笑笑家12月总支出是多少元?(写出解题过程)
24.某种子培育基地用A、B、C、D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广。通过实验得知,C型号种子的发芽率为95%。以下是根据实验数据绘制的图-1和图-2两幅尚不完整的统计图。
用于实验的各型号种子数的百分比
各型号种子的发芽情况统计图
(1)观察图-1,计算用于实验的D型号种子的粒数是多少?
(2)先计算出C型号种子发芽的粒数,然后将图-2的统计图补充完整。
(3)应选( )型号的种子进行推广(将种子的型号直接填在括号内)。
25.某小学对本校若干名学生和部分家长对“小学生在校吃零食”现象进行了调查,并根据调查结果制作了统计图。请回答下列问题:
(1)参加调查的家长( )人。
(2)请补全条形统计图。
(3)下图是根据家长的调查情况制作的扇形统计图,请你在扇形统计图中完成填空。
(4)从这次接受调查的家长中任意抽查一名家长,抽到持哪类态度的可能性大?
26.小华家去年支出情况如图所示,若小华家去年衣食住行用去4.5万元.那么他家去年存入银行的钱有多少万元?
27.下图是根据六年级1班一次数学测试成绩数据绘制成的统计图,请结合两幅统计图提供的信息,回答下面问题。
(1)优秀人数比及格人数多__________;
(2)六年级1班有__________人参加本次数学测试;
(3)本次测试的优秀率是__________,不及格占本测试人数的__________;
(4)把条形统计图和扇形统计图补充或填写完整。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】题干未明确说明甲班和乙班人数相同,可知它们的单位“1”不一定相同,即可得出答案。
【详解】因为单位“1”不一定相同,所以无法比较两个班男生人数的多少。
故答案为:C。
【点睛】根据扇形统计图,考察学生对单位“1”的理解。
2.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】2020年上半年兴义市生产总值为204.08亿元,如果想要表示劳动报酬、生产税净额、营业盈余等与生产总值的关系,选择扇形统计图更合适。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
3.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况解答即可。
【详解】A.小明6~12岁的身高变化最适合用折线统计图表示。
B.牛奶的营养成分最适合用扇形统计图表示。
C.小红5次数学检测的成绩最适合用条形统计图表示。
D.某班男生的体重最适合用条形统计图表示。
故答案为:B
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
4.C
【详解】由统计图知,环境保护问题的电话占本周内接到的热线电话量的35%,根据求一个数的百分之几是多少,把本周内接到的热线电话量看作单位“1”,求单位“1”用除法计算。
70÷35%=200(个)
故答案为:C
【点睛】考查了有关扇形统计图的知识,分析图中的数据,找出相关的量进行解答。
5.B
【解析】以一个圆的面积表示育新小学六年级学生喜欢的运动项目的情况,以扇形面积表示各种运动占的百分比。从图上能够读出各种运动所占的百分比,例如足球占的百分比为20%,我们还知道喜欢足球这项运动的学生有40人,两者相结合可以求出这次调查的学生总数。再结合跳绳所占的百分比:15%,能够求出喜欢跳绳的人数。
【详解】A:12.5%<15%<20%<22.5%<30%,所以喜欢踢毽子的人数所占百分比最少,但其他中的类型和占总人数的百分数都不知道,所以无法判断最少,A错;
B:用喜欢足球的人数除以它所占的百分比可得出总人数:
40÷20%=40÷0.2=200(人)
用总人数乘喜欢跳绳的百分比就得出喜欢跳绳的人数:
200×15%=200×0.15=30(人)B对;
C:12.5%<15%<20%<22.5%<30%,但其他中的类型和占总人数的百分数都不知道,所以无法判断最多;C错。
故答案为:B。
【点睛】数据统计的全过程有收集数据、整理数据、绘制图表、分析数据、得出结论五个环节。建立数据分析观念最好的办法是让学生经历统计的全过程。即让学生经历完整的收集、整理、描述、分析的统计全过程。
6.A
【分析】首先要清楚每一种统计图的特点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此求解即可。
【详解】A.各学科教师为部分,全校教师为整体,各学科教师占全校教师的百分比情况即部分与整体的关系,用扇形统计图表示最合适
B.要了解小明家5年内旅游消费增减变化情况,用折线统计图表示最合适
C.要了解华为手机和苹果手机2018年每月销售情况,用条形统计图表示最合适
D.要了解5月份气温变化情况,用折线统计图表示最合适
故答案为:A
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答,牢记它们各自的特点。
7.C
【分析】2格表示20人,那么1格表示:20÷2=10(人),因此用120除以10即可。
【详解】120÷10=12(格)
故答案为:C
【点睛】熟练掌握单式条形统计图的特点是解答此题的关键。
8.D
【分析】题目中已给出部分与总体的百分比,四个选项用阴影表示圆心角,可以结合圆周角360°计算出这部分所占圆心角的度数,再与四个选项相比较,可以得出答案。
【详解】360°×27.1%=97.56°
97.56°>90°
通过观察各扇形的圆心角发现,A、B、C三个扇形的圆心角均小于90°,
因此,只有D能正确表示这个百分比。
故答案为:D
【点睛】本题还有一种简单的做法:因为百分比27.1%>25%(),故只要观察四个选项中哪个图的阴影部分所占面积>,即可确定该选项是对的。
9. 条形 折线 扇形 扇形
【分析】条形统计图的特点:用直条的长短表示数量的多少,从图中直观地看出数量的多少,便于比较;
折线统计图的特点:不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况;
扇形统计图的特点:能清楚地看出各部分数量与总数量之间,部分与部分之间的关系。
【详解】常见的统计图有条形统计图、折线统计图、扇形统计图,为反映各部分在总体中所占的百分比,一般选择扇形统计图。
【点睛】明确各种统计图的特点是解答本题的关键。
10. 圆 扇形 各部分 整体
【详解】由扇形统计图的特点可知:扇形统计图用整个圆表示总数,用圆内各个扇形的大小表示各部分在总体中所占的百分比,通过扇形统计图可以很清楚地表示出各部分与整体间的关系。
11.各部分
【详解】根据扇形统计图的特点,扇形统计图能反映各部分与整体的关系。因此,扇形统计图可以直观、清楚地表示出各部分占总体的百分之多少。
12.扇形
【分析】条形统计图能表示数量的多少;折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;扇形统计图表示部分与整体之间的关系。
【详解】为了表示出各民族学生占的比例,因为要表示部分与整体之间的关系,所以可以选用扇形统计图。
故答案为:扇形。
【点睛】本题考查的是扇形统计图的特征,关键审清题意看需要做出什么样的效果。
13. 31.8 19.2
【分析】把整个鸡蛋的质量看作单位“1”,其中蛋白约占53%,蛋黄约占32%,根据求一个数的百分之几是多少,用乘法解答。
【详解】0.06千克=60克
60×53%=31.8(克)
60×32%=19.2(克)
即丽丽每天摄入的蛋白有31.8克,蛋黄有19.2克。
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,再根据求一个数的百分之几是多少的方法解决问题。
14. 能很容易看出数量的多少 能反映部分与整体的关系
【分析】根据统计图的特点填空即可。
【详解】条形统计图的特点是能很容易看出数量的多少,折线统计图的特点是不仅能看出数量的多少,而且能反映数量的增减变化情况,扇形统计图特点是能反映部分与整体的关系。
【点睛】此题考查了统计图的特点,需要牢记。
15. 折线 扇形
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】由分析得:
“接种新冠疫苗,共筑免疫长城”,如果要反映每日接种疫苗人数增减变化情况,应选用折线统计图,如果要反映各省接种疫苗人数与全国接种疫苗人数之间的关系,应选用扇形统计图。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
16.扇形
【解析】略
17.√
【详解】扇形统计图清楚地看出各部分数量与总数量之间,部分与部分之间的关系,原题说法正确;
故答案为:√。
18.√
【详解】略
19.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映各部分数量与总数之间的关系;根据统计图的特点选择合适的统计图。
【详解】根据统计图的特点可知:要表示某种矿泉水中各种矿物质的含量占总量的多少,选用扇形统计图比较合适。
故答案为:×
【点睛】掌握条形统计图、折线统计图、扇形统计图的特点是解题的关键。
20.×
【详解】略
21.见详解
【分析】参加调查的总人数=参加跳绳的人数÷占的百分率;参加其它各项的人数=参加调查的总人数×各自占的百分率,然后依据计算出的人数画出直条,标上数据。
【详解】70÷35%=200(人)
200×25%=50(人)
200×30%=60(人)
200-70-50-60
=130-50-60
=80-60
=20(人)
【点睛】本题考查的是扇形统计图和条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据。
22.(1)扇形
(2)45,5∶9∶6
(3)120人
【分析】(1)通过观察发现此统计图把圆分成几个扇形,据此可解答。
(2)把整个圆看作单位“1”,用单位“1”减去其余的两部分的占比即可;根据比的基本性质化简即可。
(3)用总人数×假性近视所占的比重=假性近视的人数,据此可解答。
【详解】1)这是扇形统计图。
(2)1-25%-30%
=75%-30%
=45%
25%∶45%∶30%
=25∶45∶30
=5∶9∶6
(3)400×30%=120(人)
【点睛】本题考查扇形统计图,明确由整体求部分用乘法是解题的关键。
23.(1)20;生活支出;
(2)1000元
【分析】(1)根据扇形统计图的信息 ,确定文化支出所占的百分比,再根据百分数比较大小的方法比较各项支出所占的百分比,据此确定占比最大的支出。
(2)根据扇形统计图可知,生活支出比文化支出多(46%-20%),再根据已知一个数的百分之几是多少,求这个数用除法列式计算即可。
【详解】(1)文化支出占总支出的20%;
8%<16%<20%<46%
所以:几项支出中,占比最大的支出是生活支出。
(2)260÷(46%-20%)
=260÷26%
=1000(元)
答:笑笑家12月总支出是1000元。
【点睛】能读懂扇形统计图中的信息是解答本题的关键。
24.(1)500粒;
(2)380粒;图见详解;
(3)C
【分析】(1)求出D所占的百分比,进而求出D的种子粒数;
(2)求出C的种子粒数,进而求出发芽粒数,补充完整;
(3)分别求出A、B、D发芽率,发芽率高的进行推广;据此解答。
【详解】(1)(1-20%-20%-35%)×2000
=0.25×2000
=500(粒)
答:用于实验的D型号种子的粒数是500粒。
(2)2000×20%×95%
=400×0.95
=380(380)
补充如下:
(3)A发芽率:630÷(2000×35%)×100%
=630÷700
=90%
B发芽率:370÷(2000×20%)×100%
=370÷400
=92.5%
C发芽率:95%
D发芽率:470÷500×100%
=0.94×100%
=94%
90%<92.5%<94%<95%,所以应选C型号的种子进行推广。
【点睛】本题主要考查统计图的综合应用。
25.(1)100;
(2)见详解;
(3)见详解;
(4)反对
【分析】(1)参加调查的家长人数是20人,占调查家长人数的20%,根据分数除法的意义,用20÷20%求出参加调查家长的人数;
(2)参加调查家长的总人数-赞成的人数-无所谓的人数=反对的人数;
(3)用赞成的人数、反对的人数分别除以总人数,求出百分率即可;
(4)哪种所占百分率大,抽到那种的可能性就大。
【详解】(1)20÷20%=100(人)
(2)100-10-20=70(人)
补充统计图如下:
(3)10÷100=10%
70÷100=70%
补充统计图如下:
(4)70%>20%>10%
答:抽到反对态度的可能性大。
【点睛】本题主要考查统计图表的综合应用。
26.4.5÷45%×20%=2(万元)
答:存入银行的钱有2万元.
【详解】略
27.(1)50
(2)40
(3)30%;5
(4)见详解
【分析】(1)根据条形统计图,可以看出成绩是优秀的有12人,及格的有8人,先计算出优秀人数比及格人数多的人数,再除以及格的人数即可得解;
(2)根据及格的有8人,以及扇形统计图及格的占总测试人数的20%,可求出测试人数为8÷20%=40(人);
(3)用优秀的人数除以参加测试的人数,就是优秀率,用总人数单位“1”分别减去优秀人数,良好人数,及格人数所占的百分率,就是不及格人数占的百分率;
(4)先计算出及格人数、不及格人数占总人数的百分率,在扇形统计图上标出,进而用总人数分别乘良好和不及格人数占的百分率,再在条形统计图上标出即可。
【详解】(1)(12-8)÷8
=4÷8
=50%
答:优秀人数比及格人数多50%。
(2)测试人数:8÷20%=40(人)
答:六年级1班有40人参加本次数学测试。
(3)优秀率:12÷40×100%=30%
1-45%-20%-30%
=55%-20%-30%
=35%-30%
=5%
答:本次测试的优秀率是30%,不及格占本班测试人数的5%。
(4)40×45%=18(人)
40×5%=2(人)
【点睛】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题。
答案第1页,共2页
答案第1页,共2页
