苏科版初二数学下册 7.2 统计图的选用(练习)(含解析)
文档属性
| 名称 | 苏科版初二数学下册 7.2 统计图的选用(练习)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 663.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 00:00:00 | ||
图片预览

文档简介
7.2 统计图的选用(专项练习)
一、单选题
1.要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比最适合采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.统计表
2.甲、乙、丙三个小组生产帐蓬,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.如图是描述三个小组一天生产帐蓬情况的统计图,从中可以得出人数最多的小组是( )
A.甲组 B.乙组 C.丙组 D.乙、丙两组
3.某校七年级开展“阳光体育”活动,对喜欢乒乓球、足球、篮球、羽毛球的学生人数进行统计(每人只能选择其中一项),得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的4倍,喜欢乒乓球的人数是21人,则下列说法正确有( )
①被调查的学生人数为70人:
②喜欢篮球的人数为14人;
③喜欢足球的扇形的圆心角为36°;
④喜欢羽毛球的人数占被调查人数的40%:
A.1个 B.2个 C.3个 D.4个
4.如图,整个圆代表八年级全体同学参加数学拓展课的总人数,其中参加“生活数学”拓展课的人数占总人数的,则图中表示“生活数学”拓展课人数的扇形是( )
A.M B.N C.P D.Q
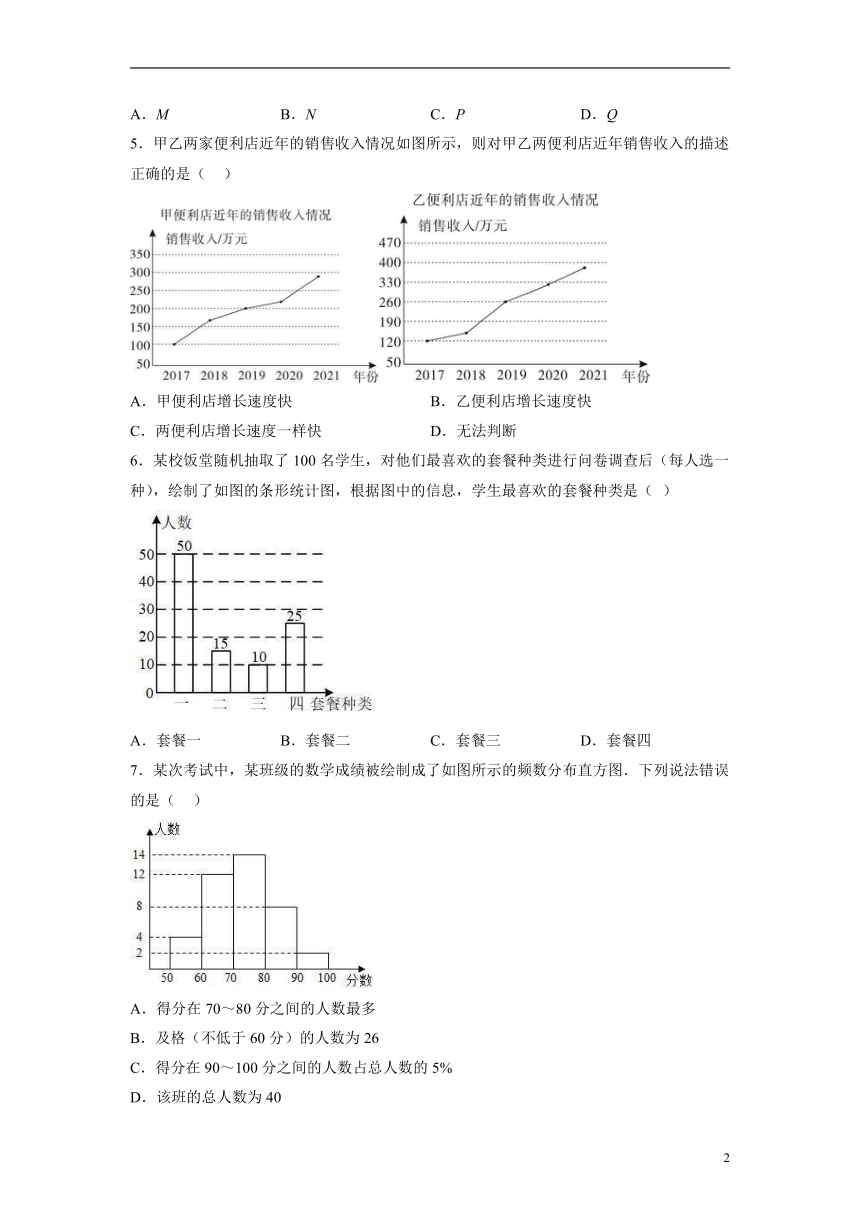
5.甲乙两家便利店近年的销售收入情况如图所示,则对甲乙两便利店近年销售收入的描述正确的是( )
A.甲便利店增长速度快 B.乙便利店增长速度快
C.两便利店增长速度一样快 D.无法判断
6.某校饭堂随机抽取了100名学生,对他们最喜欢的套餐种类进行问卷调查后(每人选一种),绘制了如图的条形统计图,根据图中的信息,学生最喜欢的套餐种类是( )
A.套餐一 B.套餐二 C.套餐三 D.套餐四
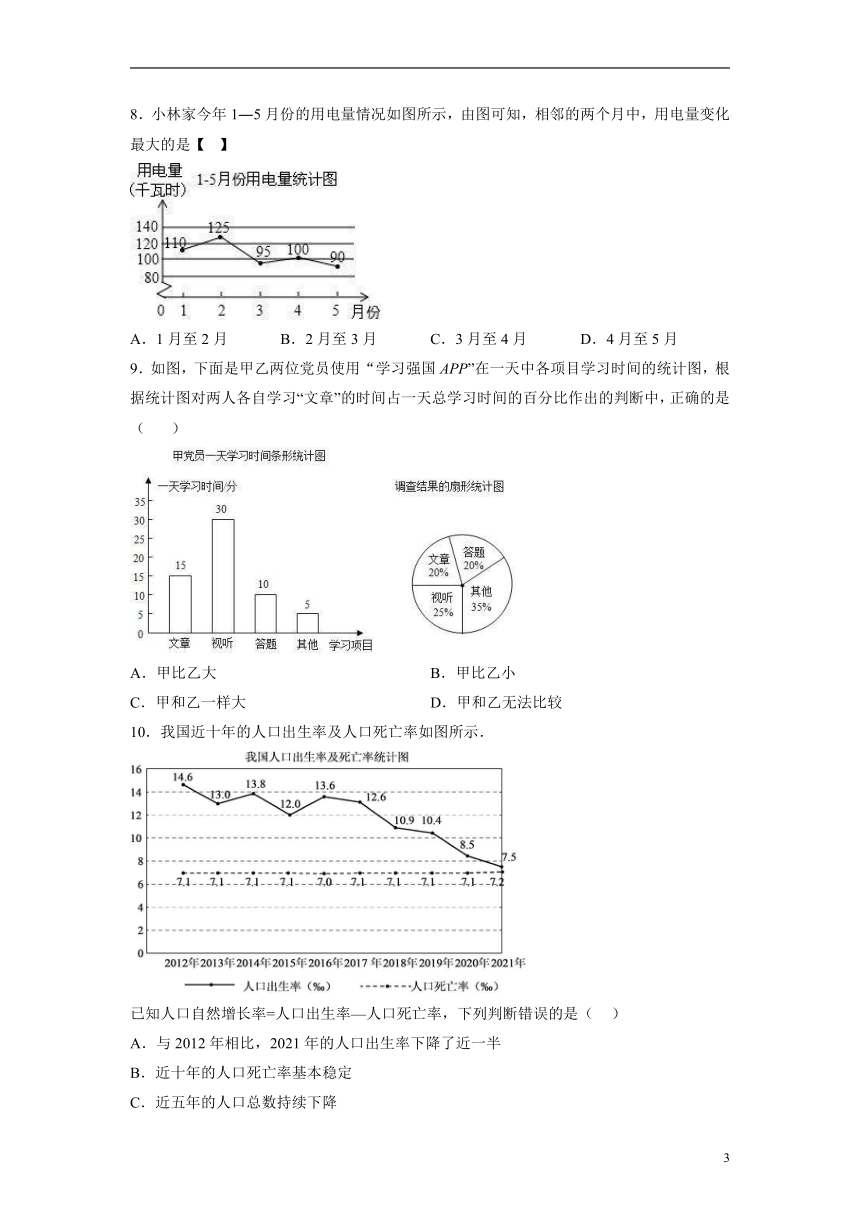
7.某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.及格(不低于60分)的人数为26
C.得分在90~100分之间的人数占总人数的5%
D.该班的总人数为40
8.小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是【 】
A.1月至2月 B.2月至3月 C.3月至4月 D.4月至5月
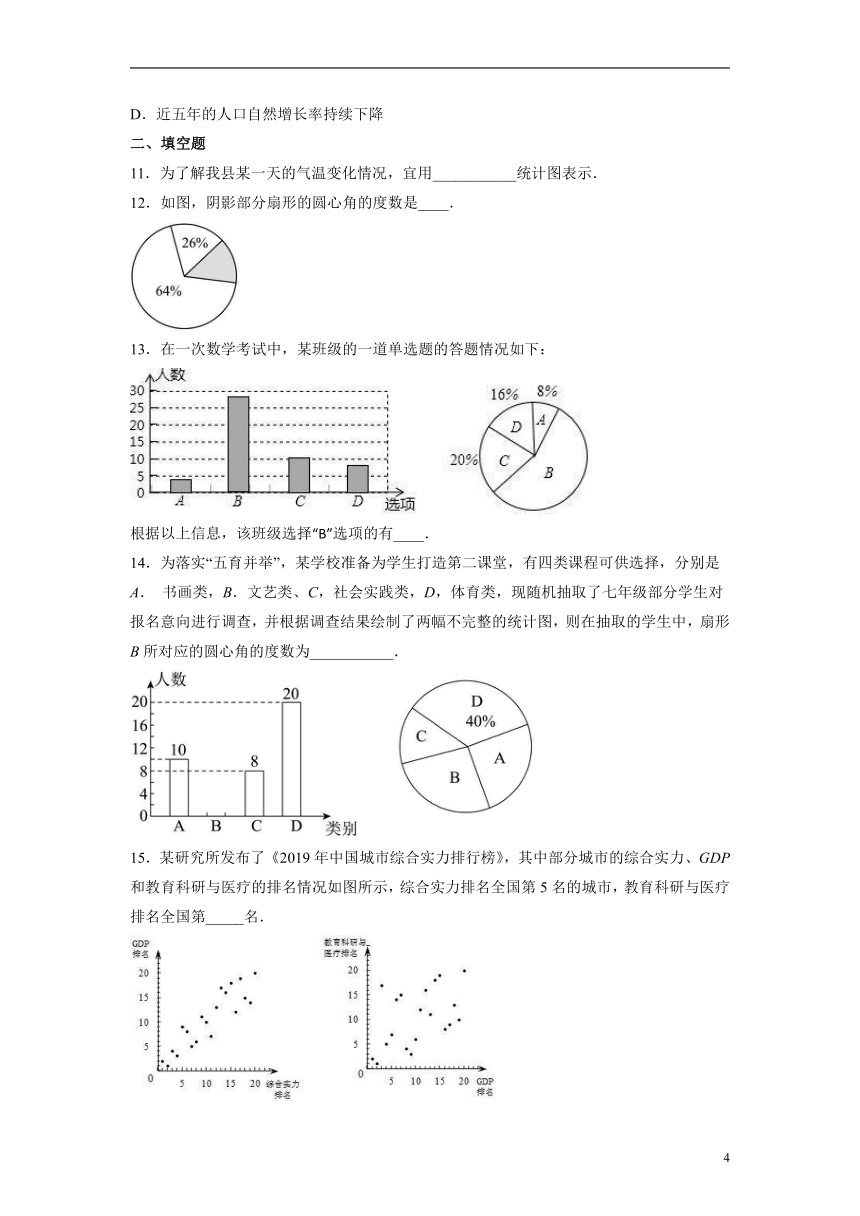
9.如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是( )
A.甲比乙大 B.甲比乙小
C.甲和乙一样大 D.甲和乙无法比较
10.我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率—人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
二、填空题
11.为了解我县某一天的气温变化情况,宜用___________统计图表示.
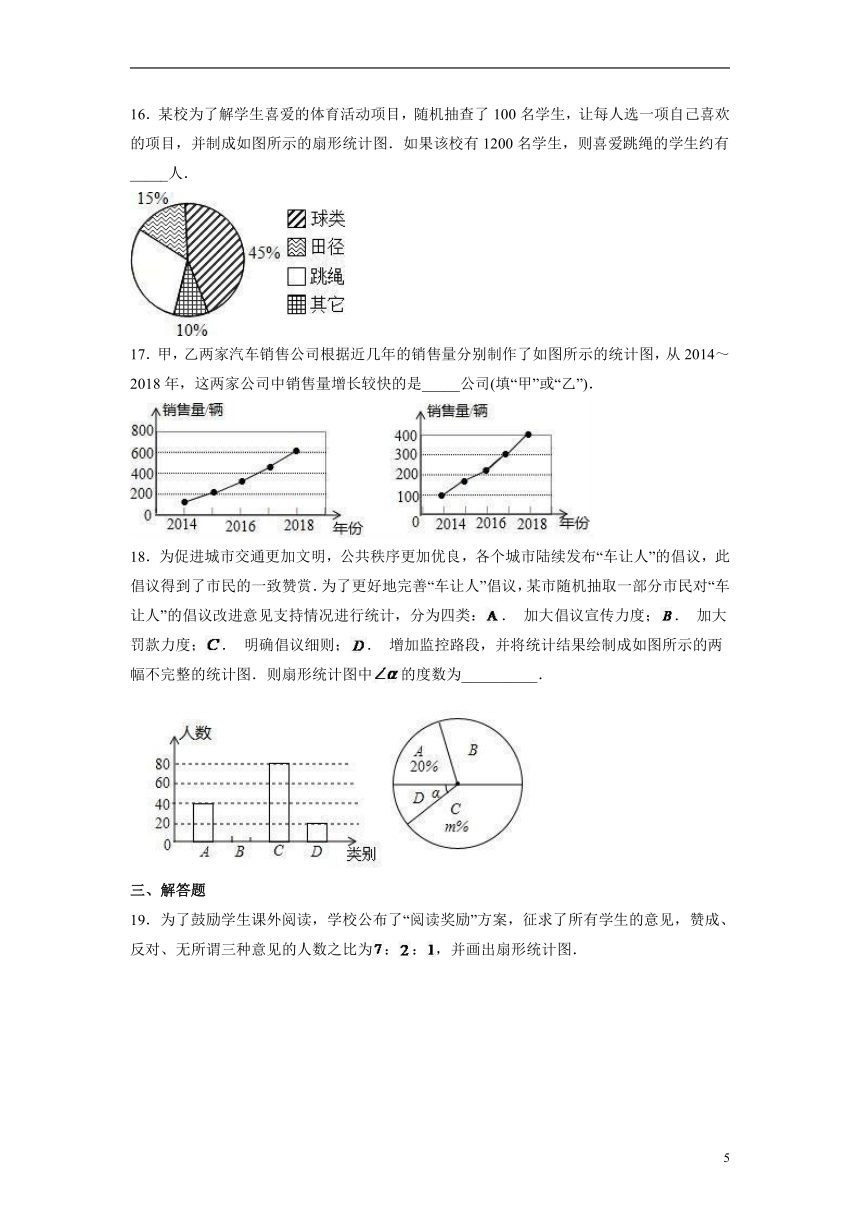
12.如图,阴影部分扇形的圆心角的度数是____.
13.在一次数学考试中,某班级的一道单选题的答题情况如下:
根据以上信息,该班级选择“B”选项的有____.
14.为落实“五育并举”,某学校准备为学生打造第二课堂,有四类课程可供选择,分别是A. 书画类,B.文艺类、C,社会实践类,D,体育类,现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,则在抽取的学生中,扇形B所对应的圆心角的度数为___________.
15.某研究所发布了《2019年中国城市综合实力排行榜》,其中部分城市的综合实力、GDP和教育科研与医疗的排名情况如图所示,综合实力排名全国第5名的城市,教育科研与医疗排名全国第_____名.
16.某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有1200名学生,则喜爱跳绳的学生约有_____人.
17.甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
18.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取一部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:. 加大倡议宣传力度;. 加大罚款力度;. 明确倡议细则;. 增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中的度数为__________.
三、解答题
19.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,赞成、反对、无所谓三种意见的人数之比为::,并画出扇形统计图.
(1)如果持反对意见的有人,那么这个学校共有多少名学生?
(2)求图中各个扇形的圆心角的度数.
20.某校决定午餐后免费供应水果以加强初中生体质.每名学生可在香蕉、苹果、梨子中任选一样,现从全校学生中随机抽取部分学生进行调查,并将调查结果绘制成了如图所示的统计图(部分信息未给出).已知被调查的男生人数为100人,选择梨子的女生人数是选择梨子的男生人数的2倍,选择香蕉的女生人数是选择苹果的女生人数的3倍.
(1)求被调查学生的总人数;
(2) 补全条形统计图和扇形统计图.
21.为了解疫情期间学生网络学习的学习效果,我校随机抽取了九年级部分学生进行调查.调查结果分为四类:A类为“优秀”,B类为“良好”,C类为“一般”,D类为“不合格”,现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1) 本次共调查了 ___________名学生;
(2) 补全条形统计图:D类所对应扇形的圆心角的大小为 ___________;
(3) 若我校九年级学生共有1700名,根据以上抽样结果,估计我校九年级学生学习效果为“优秀”的学生约有多少名?
22.学校在“2019中华经典诵读”活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)调查中B等级有多少人?将图甲中的折线统计图补充完整;
(3)求出图乙中B等级所占圆心角的度数.
23.某商店试销A、B两款电视机,四个月共售出400台.试销结束后,该商店想从中选择一款电视机进行经销.请根据提供的两幅统计图完成下列问题:
(1)第四个月销量占总销量的百分比是______%;
(2)求出第三个月B款电视机的销量,并在图2中补全B款电视机月销量的折线图;
(3)结合折线图,判断该商店应选择哪款电视机进行经销?请说明理由.
24.某校为了解落实“双减”政策后学生每天完成书面作业的时间t(单位:分钟)的情况,在全校随机抽取部分小学生进行调查,按四个组别进行整理,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生作业时间统计表
组别 调查结果 人数(人)
A 120
B a
C 180
D 90
(1)这次调查抽取学生的总人数是_______,B组的学生人数______;
(2)该校共有学生1500人,请估算该校每日书面作业时间不少于90分钟的学生人数;
(3)请结合数据对该校“双减”工作提出一条合理性建议.
参考答案
1.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【详解】解:根据统计图的特点可知:要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比,那么应该选用扇形统计图更合适.
故选:B.
【点拨】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
2.C
【分析】根据统计图数据,分别求出甲、乙、丙三组的男工人与女工人数,然后比较即可.
【详解】解∶甲组男工人的人数为人,女工人的人数为人,
∴甲组的人数18+6=24人;
乙组男工人的人数为人,女工人的人数为人,
∴乙组的人数16+9=25人;
丙组男工人的人数为人,女工人的人数为人,
∴丙组的人数8+18=26人;
∴丙组的人数最多.
故选:C
【点拨】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
3.D
【分析】根据喜欢乒乓球的人数和所占的百分比求出总人数,即可判断①;用总人数乘以喜欢篮球的人数所占的百分比,即可判断②;根据喜欢羽毛球的人数是喜欢足球的人数的4倍,求出喜欢足球的人数,然后用360°乘以喜欢足球的人数所占的百分比,即可判断③;用喜欢羽毛球的人数除以总人数,即可判断④.
【详解】解:①被调查的学生人数为:21÷30%=70(人),故说法正确;
②喜欢篮球的人数为:70×20%=14(人),故说法正确;
③喜欢羽毛球和足球的人数为:70×(1-20%-30%)=35人,因为喜欢羽毛球的人数是喜欢足球的人数的4倍,所以喜欢足球的人数为:35×=7人,喜欢足球的扇形的圆心角为360°×=36°,故说法正确;
④羽毛球的人数为28人,占被调查人数的×100%=40%,故说法正确;
综上,四个选项都是正确的,
故选:D.
【点拨】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
4.A
【分析】首先根据扇形Q的圆心角为可得参加此类课的人数约占总数的,再根据,可得扇形的面积一定比Q大,根据图可选出答案.
【详解】解:∵扇形Q的圆心角为,
∴表示参加此类课的人数占总数的:,
∵,
∴扇形的面积一定比Q大,
∴图中表示“生活数学”拓展课人数的扇形是M,
故选:A.
【点拨】此题主要考查了扇形统计图,关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
5.B
【分析】观察图形可得甲便利店从2017年到2021年销售收入在150万元和200万元之间;乙便利店从2017年到2021年销售收入在210万元和280万元之间,即可求解.
【详解】解:根据题意得:
甲便利店:2017年销售收入为100万元,2021年销售收入在250万元和300万元之间;
乙便利店:2017年销售收入为120万元,2021年销售收入在330万元和400万元之间;
∴甲便利店从2017年到2021年销售收入在150万元和200万元之间;乙便利店从2017年到2021年销售收入在210万元和280万元之间,
∴乙便利店增长速度快.
故选:B
【点拨】本题主要考查了折线统计图,明确题意,准确从统计图获取信息是解题的关键.
6.A
【分析】通过条形统计图可以看出套餐一出现了50人,最多,即可得出答案.
【详解】解:通过观察条形统计图可得:套餐一一共出现了50人,出现的人数最多,因此通过利用样本估计总体可以得出学生最喜欢的套餐种类是套餐一;
故选:A.
【点拨】本题主要考查了条形统计图,明白条形统计图能清楚地表示出每个项目的数据,从条形统计图中得到必要的信息是解决问题的关键.
7.B
【分析】根据频数分布直方图得出各分数段内的人数,再据此对各选项逐一判断即可.
【详解】A.得分在70~80分之间的人数最多,有14人,故此选项正确,不符合题意,
B.及格(不低于60分)的人数为12+14+8+2=36(人),故此选项错误,符合题意,
C.∵总人数为4+12+14+8+2=40(人),得分在90~100分之间的人数为2人,
∴得分在90~100分之间的人数占总人数的百分比为×100%=5%,故此选项正确,不符合题意;
D.该班的总人数为40,故此选项正确,不符合题意,
故选:B.
【点拨】本题考查条形统计图,正确提取图中信息是解题关键.
8.B
【详解】根据折线图的数据,分别求出相邻两个月的用电量的变化值,比较即可得解:
1月至2月,125-110=15千瓦时;2月至3月,125-95=30千瓦时;
3月至4月,100-95=5千瓦时;4月至5月,100-90=10千瓦时,
所以,相邻两个月中,用电量变化最大的是2月至3月.故选B
9.A
【分析】由扇形统计图可知,乙党员学习文章时间的百分比是20%,再由条形统计图求出甲党员学习文章的百分比,进行比较即可.
【详解】由扇形统计图可知,乙党员学习文章时间的百分比是20%,
由条形统计图求出甲党员学习文章的百分比是15÷(15+30+10+5)=25%,
所以甲党员的百分比比乙党员的百分比大.
故选A.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
10.C
【分析】根据折线统计图逐项分析判断即可求解.
【详解】解:A. 与2012年相比,2021年的人口出生率下降了近一半,故该选项正确,不符合题意;
B. 近十年的人口死亡率基本稳定,故该选项正确,不符合题意;
C. 近五年的人口总数持续上升,只是自然增长率在变小,故该选项不正确,符合题意;
D. 近五年的人口自然增长率持续下降,故该选项正确,不符合题意.
故选C.
【点拨】本题考查了折线统计图,从统计图获取信息是解题的关键.
11.折线
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数据.
【详解】解:根据题意,得
要求直观反应某县某一天的气温变化情况,结合统计图各自的特点,应选择折线统计图.
故答案为:折线
【点拨】本题考查了扇形统计图、折线统计图,条形统计图各自的特点.
12.##36度
【分析】根据圆周角乘以扇形所占圆的面积的比,可得答案.
【详解】解:;
故答案为:.
【点拨】本题考查了认识平面图形,利用圆周角乘以扇形扇形所占圆的面积的比是解题关键.
13.28人.
【详解】解:10÷20%×(1-8%-16%-20%)=28人,故该班级选择“B”选项的有28人,故答案为28人.
点拨:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
14.##86.4度
【分析】用D的人数除以得出总人数,再用总人数分布及其他三类人数可得B类人数,然后用乘B类人数所占比例即可.
【详解】解:总人数为:(人),
B类人数为:(人),
所以扇形B所对应的圆心角的度数为:.
故答案为:.
【点拨】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与之比.
15.3
【分析】由第一个图可得综合实力排名全国第5名的城市的GDP排名第九,再由第二个图可求解.
【详解】解:由第一个图可得综合实力排名全国第5名的城市的GDP排名第九,
由第二个图可得GDP排名第九的城市的教育科研与医疗的排名为第3名,
故填3.
16.360
【分析】先根据扇形统计图求出喜爱跳绳的同学所占的百分比,再根据该校有1200名学生即可得到结论.
【详解】由扇形统计图可知,喜爱跳绳的同学所占的百分比=1 15% 45% 10%=30%
∵该校有900名学生
∴喜爱跳绳的学生约有:900×30%=270(人)
故答案为270.
【点拨】本题考查的是扇形统计图,根据扇形统计图求出喜爱跳绳的同学所占的百分比是解答此题的关键.
17.甲
【分析】根据甲,乙两公司折线统计图中2014年、2018年的销售量,计算即可得到增长量;根据两个统计图中甲,乙两公司销售增长量即可确定答案.
【详解】解:从折线统计图中可以看出:
甲公司2014年的销售量约为100辆,2018年约为600辆,则从2014~2018年甲公司增长了500辆;
乙公司2014年的销售量为100辆,2018年的销售量为400辆,则从2014~2018年,乙公司中销售量增长了300辆.
所以这两家公司中销售量增长较快的是甲公司,
故答案为甲.
【点拨】本题考查了折线统计图的相关知识,由统计图得到关键信息是解题的关键;
18.
【分析】利用A的人数除以所占总数的百分比求出总数,再求出D的百分数,再求对应角度即可得结论.
【详解】解:由题意总数(本),
∵D占,
∴圆心角,
故答案为:.
【点拨】本题考查条形统计图,条形统计图等知识,解题的关键是知道圆心角=360°×百分比.
19.(1)这个学校共有1200名学生;
(2)赞成对应的圆心角的度数为252°,反对对应的圆心角的度数为 72°,无所谓对应的圆心角的度数为36°.
【分析】(1)根据赞成、反对、无所谓三种意见的人数之比为7:2:1和持反对意见的有240人,可以计算出这个学校共有多少名学生;
(2)根据赞成、反对、无所谓三种意见的人数之比为7:2:1,可以计算出图中各个扇形的圆心角的度数.
【详解】(1)240÷=1200(名),
答:这个学校共有1200名学生;
(2)赞成对应的圆心角的度数为:360°×=252°,
反对对应的圆心角的度数为:360°×=72°,
无所谓对应的圆心角的度数为:360°×=36°.
【点拨】本题考查扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
20.(1)被调查学生的总人数为250人
(2)补全条形统计图和扇形统计图见解析
【分析】(1)根据题意得出男生选择梨子的人数,即可确定女生选择梨子的人数,得出女生总人数,由此即可求总人数;
(2)根据(1)中结果补全条形统计图,根据选择香蕉的女生人数是选择苹果的女生人数的3倍补全扇形统计图即可.
【详解】(1)男生选择梨子的有:(人),
女生选择梨子的有:(人),
女生总人数为:(人),
被调查的总人数为:(人),
即被调查的总人数为250人;
(2)由(1)可知,
男生选择梨子的有45人,
女生选择苹果的学生所占的百分比为,
选择香蕉的学生所占的百分比为,
补全的统计图如图所示.
【点拨】题目主要考查条形统计图与扇形统计图,根据两个统计图获取相关信息进行计算是解题关键.
21.(1)50
(2)
(3)510
【分析】(1)根据类的人数和所占的百分比求出抽查的总人数.
(2)用总人数减去其他类别的人数,求出类的人数,从而补全条形图;用乘以类所占百分比即可得出类所对应的扇形圆心角度数.
(3)用总人数乘以九年级学生学习效果为“优秀” 的学生人数所占的百分比即可.
(1)
这次一共抽取的学生有:
(名),
故答案为:50.
(2)
类的人数有:(名),补全统计图如下:
扇形统计图中类所对应的扇形圆心角大小为:,
故答案为:.
(3)
(名),
答:估计我校九年级学生学习效果为“优秀”的学生为510名.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用,从不同统计图中得到必要的信息是解决本题的关键.
22.(1)50
(2)20人,图见解析
(3)144°
【分析】(1)从两个统计图中可知,C等级有10人,占调查人数的20%,可求出调查人数;
(2)调查人数为50,即A、B、C、D等级的频数和为50,即可求出B等级的频数;
(3)求出B等级所占的百分比,即可求出相应的圆心角的度数.
(1)
解:10÷20%=50(名),
故答案为:50;
(2)
解:B等级人数为:50﹣15﹣10﹣5=20(人),
补全的折线统计图如图所示:
(3)
解:图乙中,B等级所占圆心角的度数为360°144°,
答:图乙中B等级所占圆心角的度数为144°.
【点拨】本题主要考查了折线统计图和扇形统计图,明确题意,准确从统计图中获取信息是解题的关键.
23.(1)30
(2)第三个月B款电视机的销量为50台;补全B款电视机月销量的折线图见解析
(3)该商店应选择B款电视机进行经销;理由是B款电视机的销量逐月递增,而A款电视机的销量有下降趋势
【分析】(1)先求第四个月的销售量,再除以总量即可得到第四个月销售量占总销售量的百分比;
(2)由折线图求得第三个月A、B两款的销售量为100台,再解得第三个月A款电视机的销量为50台,据此解出B的销售量;
(3)观察折线图可得,该商店应选择B款电视机进行经销.
(1)
解: 400×(1﹣15%﹣30%﹣25%)=120(台),
∴第四个月销量占总销量的百分比=120÷400=30%;
故答案为:30%;
(2)
第三个月A、B两款电视机的销量为400×25%=100(台),
从折线图可知,第三个月A款电视机的销量为50台,
第三个月B款电视机的销量为100﹣50=50(台);
如图
(3)
该商店应选择B款电视机进行经销;理由是B款电视机的销量逐月递增,而A款电视机的销量有下降趋势.
【点拨】本题考查折线统计图和扇形统计图的综合应用,掌握相关知识是解题关键.
24.(1)600,210
(2)该校每日作业时长不少于90分钟的学生人数为675人
(3)建议该学校作业布置要减少题量或降低难度.(答案不唯一)
【分析】(1)根据总人数=A组人数÷A组所占百分比,总人数×B组百分比,即可求出本题答案;(2)1500×不低于90分钟学生的百分比,即可求出结果;(3)合理即可.
(1)
这次调查抽取学生的总人数是600,B组的学生人数;
故答案为:600,210;
(2)
(人),
答:该校每日作业时长不少于90分钟的学生人数为675人;
(3)
该校每日作业时长不少于90分钟的学生人数占比高达45%,建议该学校作业布置要减少题量或降低难度.(答案不唯一,理由合理即可,没有结合数据得1分)
【点拨】本题考查统计表和扇形统计图,考查数据处理和分析的能力,解题关键在从不同的图中读出相应的统计量.
1
一、单选题
1.要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比最适合采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.统计表
2.甲、乙、丙三个小组生产帐蓬,已知女工人3人每天共生产4顶帐蓬,男工人2人每天共生产3顶帐蓬.如图是描述三个小组一天生产帐蓬情况的统计图,从中可以得出人数最多的小组是( )
A.甲组 B.乙组 C.丙组 D.乙、丙两组
3.某校七年级开展“阳光体育”活动,对喜欢乒乓球、足球、篮球、羽毛球的学生人数进行统计(每人只能选择其中一项),得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的4倍,喜欢乒乓球的人数是21人,则下列说法正确有( )
①被调查的学生人数为70人:
②喜欢篮球的人数为14人;
③喜欢足球的扇形的圆心角为36°;
④喜欢羽毛球的人数占被调查人数的40%:
A.1个 B.2个 C.3个 D.4个
4.如图,整个圆代表八年级全体同学参加数学拓展课的总人数,其中参加“生活数学”拓展课的人数占总人数的,则图中表示“生活数学”拓展课人数的扇形是( )
A.M B.N C.P D.Q
5.甲乙两家便利店近年的销售收入情况如图所示,则对甲乙两便利店近年销售收入的描述正确的是( )
A.甲便利店增长速度快 B.乙便利店增长速度快
C.两便利店增长速度一样快 D.无法判断
6.某校饭堂随机抽取了100名学生,对他们最喜欢的套餐种类进行问卷调查后(每人选一种),绘制了如图的条形统计图,根据图中的信息,学生最喜欢的套餐种类是( )
A.套餐一 B.套餐二 C.套餐三 D.套餐四
7.某次考试中,某班级的数学成绩被绘制成了如图所示的频数分布直方图.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.及格(不低于60分)的人数为26
C.得分在90~100分之间的人数占总人数的5%
D.该班的总人数为40
8.小林家今年1―5月份的用电量情况如图所示,由图可知,相邻的两个月中,用电量变化最大的是【 】
A.1月至2月 B.2月至3月 C.3月至4月 D.4月至5月
9.如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是( )
A.甲比乙大 B.甲比乙小
C.甲和乙一样大 D.甲和乙无法比较
10.我国近十年的人口出生率及人口死亡率如图所示.
已知人口自然增长率=人口出生率—人口死亡率,下列判断错误的是( )
A.与2012年相比,2021年的人口出生率下降了近一半
B.近十年的人口死亡率基本稳定
C.近五年的人口总数持续下降
D.近五年的人口自然增长率持续下降
二、填空题
11.为了解我县某一天的气温变化情况,宜用___________统计图表示.
12.如图,阴影部分扇形的圆心角的度数是____.
13.在一次数学考试中,某班级的一道单选题的答题情况如下:
根据以上信息,该班级选择“B”选项的有____.
14.为落实“五育并举”,某学校准备为学生打造第二课堂,有四类课程可供选择,分别是A. 书画类,B.文艺类、C,社会实践类,D,体育类,现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,则在抽取的学生中,扇形B所对应的圆心角的度数为___________.
15.某研究所发布了《2019年中国城市综合实力排行榜》,其中部分城市的综合实力、GDP和教育科研与医疗的排名情况如图所示,综合实力排名全国第5名的城市,教育科研与医疗排名全国第_____名.
16.某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有1200名学生,则喜爱跳绳的学生约有_____人.
17.甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
18.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取一部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:. 加大倡议宣传力度;. 加大罚款力度;. 明确倡议细则;. 增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中的度数为__________.
三、解答题
19.为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,征求了所有学生的意见,赞成、反对、无所谓三种意见的人数之比为::,并画出扇形统计图.
(1)如果持反对意见的有人,那么这个学校共有多少名学生?
(2)求图中各个扇形的圆心角的度数.
20.某校决定午餐后免费供应水果以加强初中生体质.每名学生可在香蕉、苹果、梨子中任选一样,现从全校学生中随机抽取部分学生进行调查,并将调查结果绘制成了如图所示的统计图(部分信息未给出).已知被调查的男生人数为100人,选择梨子的女生人数是选择梨子的男生人数的2倍,选择香蕉的女生人数是选择苹果的女生人数的3倍.
(1)求被调查学生的总人数;
(2) 补全条形统计图和扇形统计图.
21.为了解疫情期间学生网络学习的学习效果,我校随机抽取了九年级部分学生进行调查.调查结果分为四类:A类为“优秀”,B类为“良好”,C类为“一般”,D类为“不合格”,现将调查结果绘制成如图不完整的统计图,请根据统计图中的信息解答下列问题:
(1) 本次共调查了 ___________名学生;
(2) 补全条形统计图:D类所对应扇形的圆心角的大小为 ___________;
(3) 若我校九年级学生共有1700名,根据以上抽样结果,估计我校九年级学生学习效果为“优秀”的学生约有多少名?
22.学校在“2019中华经典诵读”活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请根据图中信息解答下列问题:
(1)共抽取了 名学生进行调查;
(2)调查中B等级有多少人?将图甲中的折线统计图补充完整;
(3)求出图乙中B等级所占圆心角的度数.
23.某商店试销A、B两款电视机,四个月共售出400台.试销结束后,该商店想从中选择一款电视机进行经销.请根据提供的两幅统计图完成下列问题:
(1)第四个月销量占总销量的百分比是______%;
(2)求出第三个月B款电视机的销量,并在图2中补全B款电视机月销量的折线图;
(3)结合折线图,判断该商店应选择哪款电视机进行经销?请说明理由.
24.某校为了解落实“双减”政策后学生每天完成书面作业的时间t(单位:分钟)的情况,在全校随机抽取部分小学生进行调查,按四个组别进行整理,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生作业时间统计表
组别 调查结果 人数(人)
A 120
B a
C 180
D 90
(1)这次调查抽取学生的总人数是_______,B组的学生人数______;
(2)该校共有学生1500人,请估算该校每日书面作业时间不少于90分钟的学生人数;
(3)请结合数据对该校“双减”工作提出一条合理性建议.
参考答案
1.B
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【详解】解:根据统计图的特点可知:要表示一个家庭一年用于“教育”“服装”“食品”“其他”这四项的支出各占家庭本年总支出的百分比,那么应该选用扇形统计图更合适.
故选:B.
【点拨】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
2.C
【分析】根据统计图数据,分别求出甲、乙、丙三组的男工人与女工人数,然后比较即可.
【详解】解∶甲组男工人的人数为人,女工人的人数为人,
∴甲组的人数18+6=24人;
乙组男工人的人数为人,女工人的人数为人,
∴乙组的人数16+9=25人;
丙组男工人的人数为人,女工人的人数为人,
∴丙组的人数8+18=26人;
∴丙组的人数最多.
故选:C
【点拨】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据.
3.D
【分析】根据喜欢乒乓球的人数和所占的百分比求出总人数,即可判断①;用总人数乘以喜欢篮球的人数所占的百分比,即可判断②;根据喜欢羽毛球的人数是喜欢足球的人数的4倍,求出喜欢足球的人数,然后用360°乘以喜欢足球的人数所占的百分比,即可判断③;用喜欢羽毛球的人数除以总人数,即可判断④.
【详解】解:①被调查的学生人数为:21÷30%=70(人),故说法正确;
②喜欢篮球的人数为:70×20%=14(人),故说法正确;
③喜欢羽毛球和足球的人数为:70×(1-20%-30%)=35人,因为喜欢羽毛球的人数是喜欢足球的人数的4倍,所以喜欢足球的人数为:35×=7人,喜欢足球的扇形的圆心角为360°×=36°,故说法正确;
④羽毛球的人数为28人,占被调查人数的×100%=40%,故说法正确;
综上,四个选项都是正确的,
故选:D.
【点拨】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
4.A
【分析】首先根据扇形Q的圆心角为可得参加此类课的人数约占总数的,再根据,可得扇形的面积一定比Q大,根据图可选出答案.
【详解】解:∵扇形Q的圆心角为,
∴表示参加此类课的人数占总数的:,
∵,
∴扇形的面积一定比Q大,
∴图中表示“生活数学”拓展课人数的扇形是M,
故选:A.
【点拨】此题主要考查了扇形统计图,关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
5.B
【分析】观察图形可得甲便利店从2017年到2021年销售收入在150万元和200万元之间;乙便利店从2017年到2021年销售收入在210万元和280万元之间,即可求解.
【详解】解:根据题意得:
甲便利店:2017年销售收入为100万元,2021年销售收入在250万元和300万元之间;
乙便利店:2017年销售收入为120万元,2021年销售收入在330万元和400万元之间;
∴甲便利店从2017年到2021年销售收入在150万元和200万元之间;乙便利店从2017年到2021年销售收入在210万元和280万元之间,
∴乙便利店增长速度快.
故选:B
【点拨】本题主要考查了折线统计图,明确题意,准确从统计图获取信息是解题的关键.
6.A
【分析】通过条形统计图可以看出套餐一出现了50人,最多,即可得出答案.
【详解】解:通过观察条形统计图可得:套餐一一共出现了50人,出现的人数最多,因此通过利用样本估计总体可以得出学生最喜欢的套餐种类是套餐一;
故选:A.
【点拨】本题主要考查了条形统计图,明白条形统计图能清楚地表示出每个项目的数据,从条形统计图中得到必要的信息是解决问题的关键.
7.B
【分析】根据频数分布直方图得出各分数段内的人数,再据此对各选项逐一判断即可.
【详解】A.得分在70~80分之间的人数最多,有14人,故此选项正确,不符合题意,
B.及格(不低于60分)的人数为12+14+8+2=36(人),故此选项错误,符合题意,
C.∵总人数为4+12+14+8+2=40(人),得分在90~100分之间的人数为2人,
∴得分在90~100分之间的人数占总人数的百分比为×100%=5%,故此选项正确,不符合题意;
D.该班的总人数为40,故此选项正确,不符合题意,
故选:B.
【点拨】本题考查条形统计图,正确提取图中信息是解题关键.
8.B
【详解】根据折线图的数据,分别求出相邻两个月的用电量的变化值,比较即可得解:
1月至2月,125-110=15千瓦时;2月至3月,125-95=30千瓦时;
3月至4月,100-95=5千瓦时;4月至5月,100-90=10千瓦时,
所以,相邻两个月中,用电量变化最大的是2月至3月.故选B
9.A
【分析】由扇形统计图可知,乙党员学习文章时间的百分比是20%,再由条形统计图求出甲党员学习文章的百分比,进行比较即可.
【详解】由扇形统计图可知,乙党员学习文章时间的百分比是20%,
由条形统计图求出甲党员学习文章的百分比是15÷(15+30+10+5)=25%,
所以甲党员的百分比比乙党员的百分比大.
故选A.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
10.C
【分析】根据折线统计图逐项分析判断即可求解.
【详解】解:A. 与2012年相比,2021年的人口出生率下降了近一半,故该选项正确,不符合题意;
B. 近十年的人口死亡率基本稳定,故该选项正确,不符合题意;
C. 近五年的人口总数持续上升,只是自然增长率在变小,故该选项不正确,符合题意;
D. 近五年的人口自然增长率持续下降,故该选项正确,不符合题意.
故选C.
【点拨】本题考查了折线统计图,从统计图获取信息是解题的关键.
11.折线
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数据.
【详解】解:根据题意,得
要求直观反应某县某一天的气温变化情况,结合统计图各自的特点,应选择折线统计图.
故答案为:折线
【点拨】本题考查了扇形统计图、折线统计图,条形统计图各自的特点.
12.##36度
【分析】根据圆周角乘以扇形所占圆的面积的比,可得答案.
【详解】解:;
故答案为:.
【点拨】本题考查了认识平面图形,利用圆周角乘以扇形扇形所占圆的面积的比是解题关键.
13.28人.
【详解】解:10÷20%×(1-8%-16%-20%)=28人,故该班级选择“B”选项的有28人,故答案为28人.
点拨:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
14.##86.4度
【分析】用D的人数除以得出总人数,再用总人数分布及其他三类人数可得B类人数,然后用乘B类人数所占比例即可.
【详解】解:总人数为:(人),
B类人数为:(人),
所以扇形B所对应的圆心角的度数为:.
故答案为:.
【点拨】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与之比.
15.3
【分析】由第一个图可得综合实力排名全国第5名的城市的GDP排名第九,再由第二个图可求解.
【详解】解:由第一个图可得综合实力排名全国第5名的城市的GDP排名第九,
由第二个图可得GDP排名第九的城市的教育科研与医疗的排名为第3名,
故填3.
16.360
【分析】先根据扇形统计图求出喜爱跳绳的同学所占的百分比,再根据该校有1200名学生即可得到结论.
【详解】由扇形统计图可知,喜爱跳绳的同学所占的百分比=1 15% 45% 10%=30%
∵该校有900名学生
∴喜爱跳绳的学生约有:900×30%=270(人)
故答案为270.
【点拨】本题考查的是扇形统计图,根据扇形统计图求出喜爱跳绳的同学所占的百分比是解答此题的关键.
17.甲
【分析】根据甲,乙两公司折线统计图中2014年、2018年的销售量,计算即可得到增长量;根据两个统计图中甲,乙两公司销售增长量即可确定答案.
【详解】解:从折线统计图中可以看出:
甲公司2014年的销售量约为100辆,2018年约为600辆,则从2014~2018年甲公司增长了500辆;
乙公司2014年的销售量为100辆,2018年的销售量为400辆,则从2014~2018年,乙公司中销售量增长了300辆.
所以这两家公司中销售量增长较快的是甲公司,
故答案为甲.
【点拨】本题考查了折线统计图的相关知识,由统计图得到关键信息是解题的关键;
18.
【分析】利用A的人数除以所占总数的百分比求出总数,再求出D的百分数,再求对应角度即可得结论.
【详解】解:由题意总数(本),
∵D占,
∴圆心角,
故答案为:.
【点拨】本题考查条形统计图,条形统计图等知识,解题的关键是知道圆心角=360°×百分比.
19.(1)这个学校共有1200名学生;
(2)赞成对应的圆心角的度数为252°,反对对应的圆心角的度数为 72°,无所谓对应的圆心角的度数为36°.
【分析】(1)根据赞成、反对、无所谓三种意见的人数之比为7:2:1和持反对意见的有240人,可以计算出这个学校共有多少名学生;
(2)根据赞成、反对、无所谓三种意见的人数之比为7:2:1,可以计算出图中各个扇形的圆心角的度数.
【详解】(1)240÷=1200(名),
答:这个学校共有1200名学生;
(2)赞成对应的圆心角的度数为:360°×=252°,
反对对应的圆心角的度数为:360°×=72°,
无所谓对应的圆心角的度数为:360°×=36°.
【点拨】本题考查扇形统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
20.(1)被调查学生的总人数为250人
(2)补全条形统计图和扇形统计图见解析
【分析】(1)根据题意得出男生选择梨子的人数,即可确定女生选择梨子的人数,得出女生总人数,由此即可求总人数;
(2)根据(1)中结果补全条形统计图,根据选择香蕉的女生人数是选择苹果的女生人数的3倍补全扇形统计图即可.
【详解】(1)男生选择梨子的有:(人),
女生选择梨子的有:(人),
女生总人数为:(人),
被调查的总人数为:(人),
即被调查的总人数为250人;
(2)由(1)可知,
男生选择梨子的有45人,
女生选择苹果的学生所占的百分比为,
选择香蕉的学生所占的百分比为,
补全的统计图如图所示.
【点拨】题目主要考查条形统计图与扇形统计图,根据两个统计图获取相关信息进行计算是解题关键.
21.(1)50
(2)
(3)510
【分析】(1)根据类的人数和所占的百分比求出抽查的总人数.
(2)用总人数减去其他类别的人数,求出类的人数,从而补全条形图;用乘以类所占百分比即可得出类所对应的扇形圆心角度数.
(3)用总人数乘以九年级学生学习效果为“优秀” 的学生人数所占的百分比即可.
(1)
这次一共抽取的学生有:
(名),
故答案为:50.
(2)
类的人数有:(名),补全统计图如下:
扇形统计图中类所对应的扇形圆心角大小为:,
故答案为:.
(3)
(名),
答:估计我校九年级学生学习效果为“优秀”的学生为510名.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用,从不同统计图中得到必要的信息是解决本题的关键.
22.(1)50
(2)20人,图见解析
(3)144°
【分析】(1)从两个统计图中可知,C等级有10人,占调查人数的20%,可求出调查人数;
(2)调查人数为50,即A、B、C、D等级的频数和为50,即可求出B等级的频数;
(3)求出B等级所占的百分比,即可求出相应的圆心角的度数.
(1)
解:10÷20%=50(名),
故答案为:50;
(2)
解:B等级人数为:50﹣15﹣10﹣5=20(人),
补全的折线统计图如图所示:
(3)
解:图乙中,B等级所占圆心角的度数为360°144°,
答:图乙中B等级所占圆心角的度数为144°.
【点拨】本题主要考查了折线统计图和扇形统计图,明确题意,准确从统计图中获取信息是解题的关键.
23.(1)30
(2)第三个月B款电视机的销量为50台;补全B款电视机月销量的折线图见解析
(3)该商店应选择B款电视机进行经销;理由是B款电视机的销量逐月递增,而A款电视机的销量有下降趋势
【分析】(1)先求第四个月的销售量,再除以总量即可得到第四个月销售量占总销售量的百分比;
(2)由折线图求得第三个月A、B两款的销售量为100台,再解得第三个月A款电视机的销量为50台,据此解出B的销售量;
(3)观察折线图可得,该商店应选择B款电视机进行经销.
(1)
解: 400×(1﹣15%﹣30%﹣25%)=120(台),
∴第四个月销量占总销量的百分比=120÷400=30%;
故答案为:30%;
(2)
第三个月A、B两款电视机的销量为400×25%=100(台),
从折线图可知,第三个月A款电视机的销量为50台,
第三个月B款电视机的销量为100﹣50=50(台);
如图
(3)
该商店应选择B款电视机进行经销;理由是B款电视机的销量逐月递增,而A款电视机的销量有下降趋势.
【点拨】本题考查折线统计图和扇形统计图的综合应用,掌握相关知识是解题关键.
24.(1)600,210
(2)该校每日作业时长不少于90分钟的学生人数为675人
(3)建议该学校作业布置要减少题量或降低难度.(答案不唯一)
【分析】(1)根据总人数=A组人数÷A组所占百分比,总人数×B组百分比,即可求出本题答案;(2)1500×不低于90分钟学生的百分比,即可求出结果;(3)合理即可.
(1)
这次调查抽取学生的总人数是600,B组的学生人数;
故答案为:600,210;
(2)
(人),
答:该校每日作业时长不少于90分钟的学生人数为675人;
(3)
该校每日作业时长不少于90分钟的学生人数占比高达45%,建议该学校作业布置要减少题量或降低难度.(答案不唯一,理由合理即可,没有结合数据得1分)
【点拨】本题考查统计表和扇形统计图,考查数据处理和分析的能力,解题关键在从不同的图中读出相应的统计量.
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
