苏科版初二数学下册 9.4.1 矩形(培优练习)(含解析)
文档属性
| 名称 | 苏科版初二数学下册 9.4.1 矩形(培优练习)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-16 09:35:18 | ||
图片预览



文档简介
9.4.1 矩形(培优练习)
一、单选题
1.在菱形ABCD中,对角线AC与BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是 ( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
2.如图,在矩形ABCD中,点O为对角线BD的中点,过点O作线段EF交AD于F,交BC于E,OB=EB,点G为BD上一点,满足EG⊥FG,若∠DBC=30°,则∠OGE的度数为( )
A.30° B.36° C.37.5° D.45°
3.如图,在矩形中,是延长线上一点,,连接、,过点作于点,为上一点,连接,.若,,则的长为( )
A. B.8 C. D.
4.如图,在矩形中,是边上的动点,于,于,如果,那么( )
A. B.
C. D.
5.把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A. B. C. D.
6.如图,中,,,,点D是的中点,将沿翻折得到,连接,,则线段的长等于( )
A. B. C. D.
7.如图,在平面直角坐标系中,已知点A(1,1),B,C,D,把一根长为2022个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点D处,并按D→A→B→C→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
A.(1,0) B.(0,1) C. D.
8.如图,矩形纸片中,,,点E、G分别在上,将、分别沿翻折,翻折后点C与点F重合,点B与点P重合.当A、P、F、E四点在同一直线上时,线段长为( )
A. B. C. D.
9.如图.每个小正方形的边长为1,格点线段与交于点,与交于点,连接.有下列结论①;②;③;④;⑤;⑥的面积为0.75.其中正确的结论有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在中,,,斜边的两个端点分别在相互垂直的射线、上滑动,下列结论:①若、两点关于对称,则;②、两点距离的最大值为;③若平分,则;④ 四边形的面积为.其中正确结论的个数是( )
A. B. C. D.
二、填空题
11.如图,已知矩形中,与相交于,平分交于,,则的度数为_______.
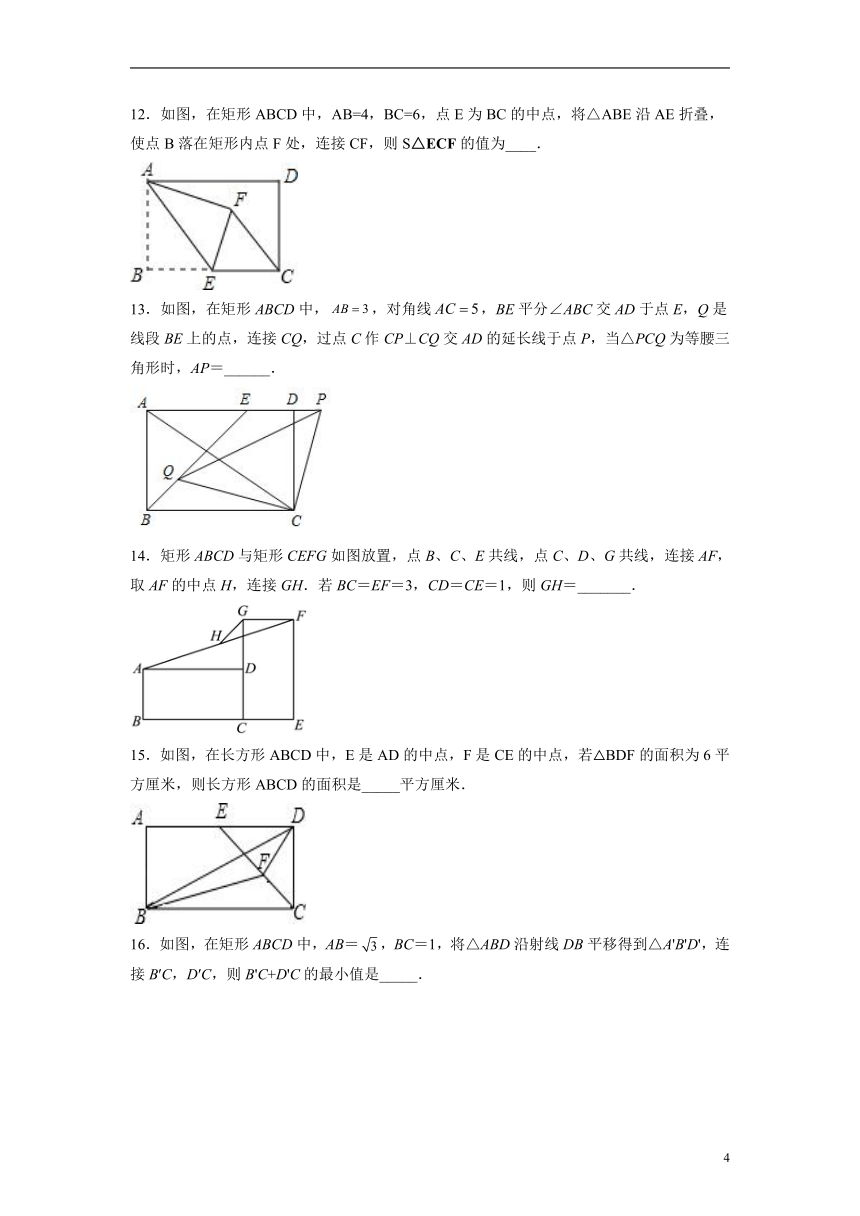
12.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为____.
13.如图,在矩形ABCD中,,对角线,BE平分∠ABC交AD于点E,Q是线段BE上的点,连接CQ,过点C作CP⊥CQ交AD的延长线于点P,当△PCQ为等腰三角形时,AP=______.
14.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH=_______.
15.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是_____平方厘米.
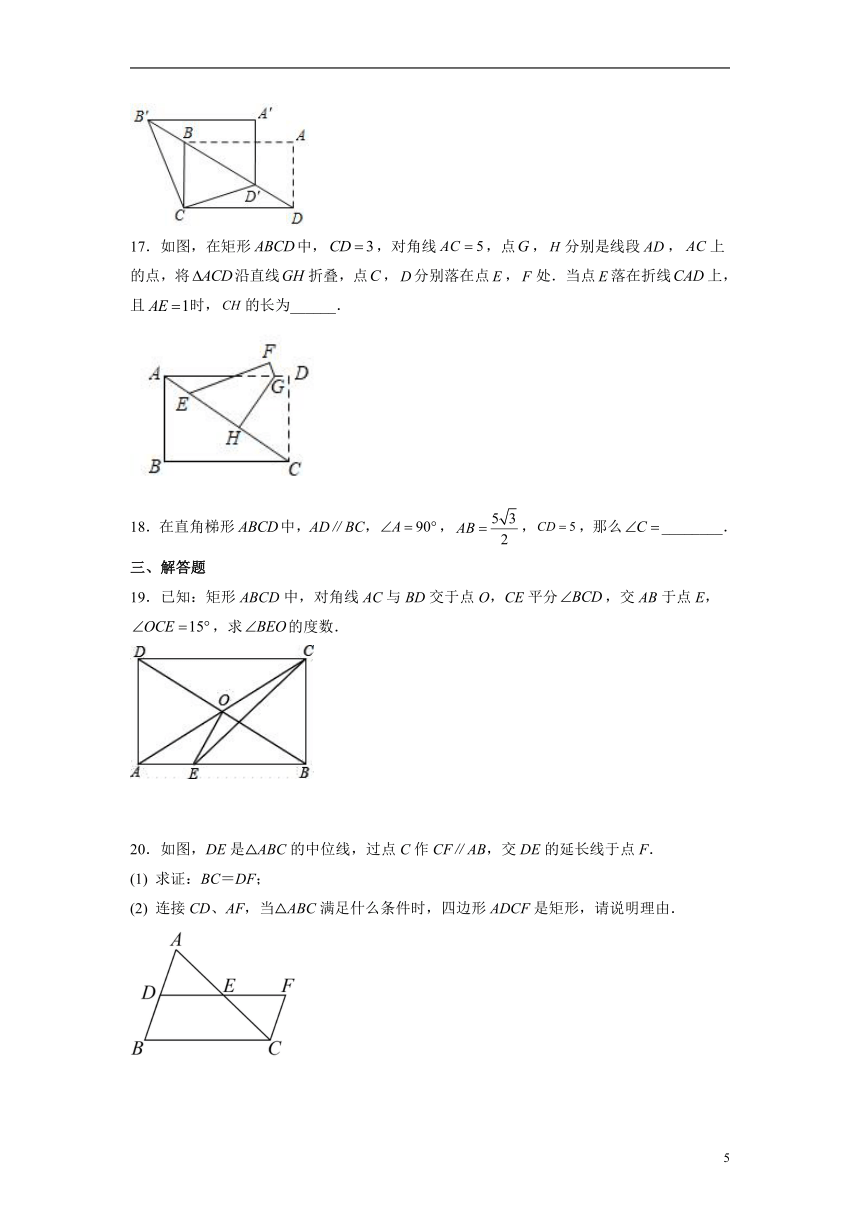
16.如图,在矩形ABCD中,AB=,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
17.如图,在矩形中,,对角线,点,分别是线段,上的点,将沿直线折叠,点,分别落在点,处.当点落在折线上,且时,的长为______.
18.在直角梯形中,AD∥BC,,,,那么________.
三、解答题
19.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分,交AB于点E,,求的度数.
20.如图,DE是△ABC的中位线,过点C作CF∥AB,交DE的延长线于点F.
(1) 求证:BC=DF;
(2) 连接CD、AF,当△ABC满足什么条件时,四边形ADCF是矩形,请说明理由.
21.将矩形置于平面直角坐标系中,点A的坐标为,点C的坐标为点,点在BC上,将矩形沿折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当时,求点E的坐标;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
22.如图,在矩形中,平分交于E,连接,.
(1) 如图1,若,,求的长;
(2) 如图2,若点F是边上的一点,若,连结交于G,
①猜想的度数,并说明理由;
②若,求的值.
23.如图,在中,,,是边上的中线,点E,F分别在,边上运动(点E不与点A,C重合),且保持,连接,,.
(1)求证:;
(2)求四边形的面积;
(3)请直接写出三条线段,,之间的数量的关系:_______.
24.如图1,在矩形中,,,点为边上一动点,连接,作点关于直线的对称点,连接,,,,与交于点.
若DE=2,求证:AE//CF.
如图2,连接AC,BD,若点F在矩形ABCD的对角线上,求所有满足条件的DE的长.
如图3,连接BF,当点F到矩形ABCD一个顶点的距离等于2时,请直接写出△BCF的面积.
参考答案
1.A
【分析】根据有一个角是直角的平行四边形是矩形,对角线相等的平行四边形是矩形,对各选项分析判断后利用排除法求解.
解:A、AB=AD,则 ABCD是菱形,不能判定是矩形,故本选项错误;
B、OA=OB,根据平行四边形的对角线互相平分,AC=BD,对角线相等的平行四边形是矩形可得 ABCD是矩形,故本选项正确;
C、AC=BD,根据对角线相等的平行四边形是矩形,故本选项正确;
D、DC⊥BC,则∠BCD=90°,根据有一个角是直角的平行四边形是矩形可得 ABCD是矩形,故本选项正确.
故选:A.
【点拨】此题考察矩形的判定,熟记判定定理才可正确解答.
2.C
【分析】根据矩形和平行线的性质,得;根据等腰三角形和三角形内角和性质,得;根据全等三角形性质,通过证明,得;根据直角三角形斜边中线、等腰三角形、三角形内角和性质,推导得,再根据余角的性质计算,即可得到答案.
解:∵矩形ABCD
∴
∴
∵OB=EB,
∴
∴
∵点O为对角线BD的中点,
∴
和中
∴
∴
∵EG⊥FG,即
∴
∴
∴
故选:C.
【点拨】本题考查了矩形、平行线、全等三角形、等腰三角形、三角形内角和、直角三角形的知识;解题的关键是熟练掌握矩形、全等三角形、等腰三角形、直角三角形斜边中线的性质,从而完成求解.
3.A
【分析】先证得△CDE是等腰直角三角形,再进一步说明∠EBC=∠CGB得到CG=BC=EG=4,说明三角形BCG为等腰三角形,进而说明GH=BH、∠CHB=90°,再根据直角三角形的性质求得CH=BC=2,进而求得GH=BH=CH=2,最后根据EH=GH+GE求解即可.
解:∵四边形ABCD是矩形
∴∠CDA=90°,AD//BC
∴∠CDE=90°,∠AEB=∠EBC=30°
∵ED=CD
∴△CDE是等腰直角三角形
∴∠DCE=∠DEC=45°
∴∠CEB=45°-30°=15°
∵EG=CG
∴∠GCE=∠GEB=15°
∴∠CGB=∠GCE+∠CEB=30°
∴∠EBC=∠CGB
∴CG=BC=4
∴EG=4
∵CH⊥BE
∴GH=BH,∠CHB=90°
∵∠EBC=30°
∴CH=BC=2,GH=BH=CH=2
∴EH=GH+EG=4+2.
故选A.
【点拨】本题主要考查了矩形的性质、等腰三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半等知识点,灵活运用相关知识点成为解答本题的关键.
4.A
【分析】设AC、BD交于点O,连接OP,根据矩形的性质及勾股定理求出OA=OD=2.5,再求出△AOD的面积,根据面积关系即可求出答案.
解:设AC、BD交于点O,连接OP,
∵,
∴BD=AC=5,
∴OA=OD=2.5,
∵,
∴,
∵于,于,
∴,
,
∴,
故选:A.
【点拨】此题考查矩形的性质,勾股定理,根据矩形的性质求出△AOD的面积是解题的关键.
5.D
【分析】如图,过点M作MH⊥A'R于H,过点N作NJ⊥A'W于J.想办法求出AR,RM,MN,NW,WD即可解决问题.
解:如图,过点M作MH⊥A'R于H,过点N作NJ⊥A'W于J.
由题意△EMN是等腰直角三角形,EM=EN=2,MN=
∵四边形EMHK是矩形,
∴EK= A'K=MH=1,KH=EM=2,
∵△RMH是等腰直角三角形,
∴RH=MH=1,RM=,同法可证NW=,
题意AR=R A'= A'W=WD=4,
∴AD=AR+RM+MN+NW+DW=4++++4=.
故答案为:D.
【点拨】本题考查翻折变换,等腰直角三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,构造特殊三角形或特殊四边形解决问题.
6.D
【分析】延长交于点,作,垂足为.首先证明垂直平分线段,是直角三角形,求出的长,在中,利用勾股定理即可解决问题.
解:如图,延长交于点,作,垂足为.
在中,,,
.
为的中点,
.
,
,
解得.
由翻折的性质可知,,
,
.
,,
.
.
根据折叠的性质有:,
,
,,
又,,
,
为直角三角形.
.
故选:D.
【点拨】本题考查翻折变换、直角三角形的斜边中线的性质、勾股定理等知识,解题的关键是学会利用面积法求高,属于中考常考题型.
7.A
【分析】先求出四边形ABCD的周长为10,得到2022÷10的余数为2,由此即可解决问题.
解:∵A(1,1),B(1,1),C(1,2),D(1,2),
∴AB∥x轴,CD∥x轴,AD∥y轴,BC∥y轴,
∴AB⊥AD,AB⊥BC,CD⊥AB,CD⊥BC,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是矩形,
∵AB=1-(-1)=2,BC=1-(-2)=3,
∴四边形ABCD的周长为:2(AB+BC)=10,
∵2022÷10=202…2,且AD=3,
∴细线另一端所在位置的点在D处上面2个单位的位置,坐标为(1,0).
故选:A.
【点拨】本题主要考查了规律型:点的坐标,解决问题的关键是熟练掌握矩形的周长公式,运用除法得到的余数确定点的位置.
8.B
【分析】根据矩形的性质得到,,,根据折叠的性质得到,,,根据勾股定理得到,设,由勾股定理列方程得到,由折叠的性质得到,,,求得,设,则,根据勾股定理列方程即可得到结论.
解:在矩形纸片中,,,
∴,,,
∵将沿翻折,翻折后点C与点F重合,
∴,,,
∴,
设,
∴,,
∵,
∴,
解得:,
∴,
∵将沿翻折,翻折后点B与点P重合,
∴,,,
∴,
设,
则,
∵,
∴,
∴,
∴线段GP长为,
故选:B.
【点拨】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,根据勾股定理列方程是解题的关键.
9.B
【分析】先证明,再逐个选项推理即可.
解:如图,
由图可得,,
∴,
∴
∵,
∴,
∴,
∴,故①正确;
∵,
∴
∴
∴,
∴,
∴,故②正确;
∵中,
∴,
∴,故③错误;
∵,,
∴,故④错误;
连接,
∵
∴,
∵,
∴,
∵,
∴
∴,故⑤正确;
∵矩形,
∴,
∵,
∴,
∴的面积为0.75,故⑥正确;
综上所述,正确的有①②⑤⑥;
故选:B.
【点拨】本题考查了全等三角形的性质与判定,矩形的性质,掌握这些性质是解决问题的关键.
10.B
解:在中,,,∴,,∴若、两点关于对称,如图,∴为的垂直平分线,∴,∴①正确;
②如图,取的中点为,连接、.
∵,∴.
当经过点时,最大且、两点距离的最大值为,∴②正确;
③如图,当,,∴四边形是矩形,∴与相互平分,但与的夹角为、,不垂直,∴③不正确;
④如图,此时四边形的面积,,∴④不正确.
综上所述:正确的有①②,个结论.故选.
点睛:本题是三角形的综合题,熟练掌握直角三角形斜边中线等于斜边一半是解答本题的关键,难度适中.
11.
【分析】先求出∠ADB,再说明三角形ODC是等边三角形,推出CD=OC,CE=CD,求出CE=OC,求出∠COE=∠OEC和∠OCB=30°即可解答.
解:∵四边形ABCD是矩形,
∴AD//BC,∠ADC=90°,OA=OC,OB=OD,AC=BD,
∵DE平分∠ADC,
∴∠ADE=∠CDE=∠ADC=45°,
∵∠BDE=15°,
∴∠ADB=∠ADE-∠BDE=30°,
∵AD∥BC,
∴∠ADB=∠DBC=30°,
∴OA=OD=OB=OC,
∴∠OBC=∠OCB=30°,
∴∠DOC=∠OBC+∠OCB=60°,
∵OD=OC,
∴△ODC是等边三角形,
∴DC=OC,
∵AD∥BC,
∴∠ADE=∠DEC
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CE=DC
∴CE=OC,
∴∠COE=∠OEC,
∵∠OCB=30°,
∴∠COE=(180°-∠OCE)=75°.
故答案为75°.
【点拨】本题考查了矩形的性质、、等边三角形的性质和判定、三角形的内角和定理等知识点,灵活应用所学知识是解答本题的关键.
12.
【分析】连接BF,根据三角形的面积公式求出BH,得到BF,根据直角三角形的判定得到∠BFC=90°,再根据勾股定理求出CF的长度,进而即可求出S△ECF.
解:如图,连接BF,
,
∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE=,
由折叠可知:BF⊥AE(对应点的连线必垂直于对称轴),
∴BH=,
∴BF=,
∵EF=BE=CE,
∴∠BFC=90°,
根据勾股定理可得:CF=,
S△ECF=S△BCF=×××=,
故答案为:.
【点拨】本题考查矩形的性质,折叠的性质,勾股定理以及三角形的面积公式,掌握知识点是解题关键.
13.5
【分析】过点Q作于点H,由矩形的性质并结合勾股定理确定,再证明以及为等腰三角形,即可推导,,然后由计算AP的长即可.
解:过点Q作于点H,如下图,
∵四边形ABCD为矩形,
∴,,,
∵,,
∴,
∵,点P在AD的延长线上,
∴,
∵△PCQ为等腰三角形,CP⊥CQ,
∴,,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∵BE平分∠ABC,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:5.
【点拨】本题主要考查了矩形的性质、全等三角形的判定与性质、勾股定理以及等腰三角形的判定与性质等知识,正确作出辅助线,构建全等三角形是解题的关键.
14.
【分析】延长GH交AD于M点,由矩形的性质得出CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,推出DG=CG-CD=2,∠HAM=∠HFG,由ASA证得△AMH≌△FGH,得出AM=FG=1,MH=GH,则MD=AD-AM=2,在Rt△MDG中,根据勾股定理得到GM,即可得出结果.
解:延长GH交AD于M点,如图所示:
∵四边形ABCD与四边形CEFG都是矩形,
∴CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,
∴DG=CGCD=3-1=2,∠HAM=∠HFG,
∵AF的中点H,
∴AH=FH,
在△AMH和△FGH中,
,
∴△AMH≌△FGH(ASA).
∴AM=FG=1,MH=GH,
∴MD=AD-AM=31=2,
在Rt△MDG中,GM=,
∴GH=GM=,
故答案为:.
【点拨】本题考查了矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质,证明三角形全等是解题的关键.
15.48
【分析】如下图,设矩形ABCD的长为m,宽为n,过点F作BC、DC的垂线,利用m、n表示出△BFD的面积,从而得出mn的大小,进而得出矩形ABCD的面积.
解:如下图,过点F作BC、CD的垂线,分别交于点Q、G,设矩形ABCD的长为m,宽为n
∵点E是AD的中点,点F是EC的中点,AD=m,AB=n
∴FQ=,FG==
∴
∴mn=48
故答案为:48
【点拨】本题考查三角形面积问题,解题关键是利用表示出△BFD的面积,从而推导出mn的大小.
16.
【分析】根据矩形的性质和勾股定理可得BD=2,即为B′D′的长,作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,则有CD′=GD′,CE⊥BD,CG=2CE,利用三角形的面积可求得CG=,然后以B′D′,GD′为邻边作平行四边形B′D′GH,可得B′H=D′G=CD′,于是当C,B′,H在同一条直线上时,CB′+B′H最短,且B'C+D'C的最小值=CH,再根据勾股定理即可求出结果.
解:∵四边形ABCD是矩形,
∴AD=BC=1,∠A=90°,
∴,
∵将△ABD沿射线DB平移得到△A'B'D',
∴B′D′=BD=2,
作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,
则CD′=GD′,CE⊥BD,CG=2CE,
∵CE=,∴CG=,
以B′D′,GD′为邻边作平行四边形B′D′GH,
则B′H=D′G=CD′,
∴当C,B′,H在同一条直线上时,CB′+B′H最短,
则B'C+D'C的最小值=CH,
∵四边形B′D′GH是平行四边形,
∴HG=B′D′=2,HG∥B′D′,
∴HG⊥CG,
∴CH=.
故答案为:.
【点拨】本题考查了矩形的性质、轴对称的性质、平移的性质、平行四边形的性质和勾股定理等知识,具有一定的难度,利用轴对称和平移的思想把所求B'C+D'C的最小值转化为求CB′+B′H的最小值是解题的关键.
17.2或
【分析】分两种情况讨论,由折叠的性质和勾股定理可求解.
解:,,
,
当点落在上时,
将沿直线折叠,
,
,
,
;
当点落在上时,如图2,连接,过点作于,
,
,
,
,
,
将沿直线折叠,
,
,
,
,
综上所述:的长为2或.
【点拨】本题考查了矩形的性质,折叠的性质,勾股定理等知识,利用勾股定理列出方程是解题的关键.
18.或##或
【分析】该题根据题意分为两种情况,首先正确画出图形,根据已知易得的直角边和斜边的长,然后利用直角三角形斜边中线等于斜边一半得到等边三角形,进而即可求解.
解:∠C存在两种情况:
①当为锐角时,如图,过作,垂足为,取的中点,连接,
,,
,
,
四边形是矩形,
,
,
,
∵,,
∴,
∴,
∴;
②当为钝角时,如图,过作,垂足为,取的中点,连接,
同理①可得,
又∵,
.
∴
综上,或,
故答案为或.
【点拨】该题重点考查了直角三角形的性质和等边三角形判定和性质,解决该题的关键一是:能根据题意画出两种情况,二是:把该题转化为直角三角形问题,从而即可求解.
19.75°
【分析】根据矩形的性质及CE平分得到∠BEC=∠BCE=∠DCE=45°,得到BE=BC,利用由此得到∠BAC=30°,根据矩形的性质证得△OBC是等边三角形,得到BC=OB=BE,由∠EBO=∠BAC=30°求出答案.
解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,OA=OB=OC=OD,CD∥AB,
∵CE平分,
∴∠BCE=∠DCE=45°,
∵CD∥AB,
∴∠BEC=∠BCE=∠DCE=45°,
∴BC=BE,
∵,
∴∠BAC=30°,
∴∠ACB=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=BE,
∵∠EBO=∠BAC=30°,
∴∠BEO=,
故答案为:75°.
【点拨】此题考查矩形的性质,等边三角形的判定及性质,等腰三角形等边对等角的性质,角平分线的性质,题中证得BE=OB是解题的关键.
20.(1)见分析 (2)当BC=AC时,四边形ADCF是矩形,理由见分析.
【分析】(1)用平行四边形的定义判定;
(2)当BC=AC时,四边形ADCF是矩形.用DE是三角形中位线证明BD=AD,用四边形DBCF是平行四边形得到CF∥BD,CF=BD,得到AD=CF,推出四边形ADCF是平行四边形,根据AC=BC,BC=DF,得到AC=DF,从而平行四边形ADCF是矩形.
解:(1)∵DE是△ABC的中位线,
∴2DE=BC,DE∥BC,
∵CF∥AB,
∴四边形DBCF是平行四边形,
∴BC=DF;
(2)当BC=AC时,四边形ADCF是矩形,理由如下:
∵DE是△ABC的中位线,
∴DB=AD,
∵四边形DBCF是平行四边形,
∴DB=CF,
∴AD=CF,
∵AB∥CF,
∴四边形ADCF是平行四边形,
∵BC=AC,BC=CF,
∴AC=DF,
∴平行四边形ADCF是矩形.
【点拨】本题主要考查了三角形中位线,平行四边形,熟练掌上三角形中位线性质,平行四边形的判定和性质,是解决此类问题的关键.
21.(1). (2)点E能恰好落在x轴上.
【分析】(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段和的长,然后利用勾股定理得到有关m的方程,求得m的值即可.
解:(1)当时,点B的坐标为,
∴,
∴是等腰直角三角形,
∴,则,
∴,
则E在y轴上,且,
∴,则点E的坐标为.
(2)点E能恰好落在x轴上.
理由如下:
∵四边形为矩形,
∴,,
由折叠的性质可得:,.
假设点E恰好落在x轴上,则,
即,
则.
在中,即,
即,解得.
【点拨】本题考查了翻折变换的性质、矩形的性质、勾股定理、坐标与图形性质、等腰直角三角形的判定与性质等知识;熟练掌握翻折变换的性质和勾股定理是解题的关键.
22.(1) (2)①,理由见分析;②
【分析】(1)由矩形的性质得,,,由角平分线的性质得出,则是等腰直角三角形,得出,推出,由勾股定理得出;
(2)①连接,由(1)得,,由证得,得出,,证明是等腰直角三角形,即可得出结论;
②根据矩形的性质得到,求得,过D作于M,根据余角的性质得到,得到,过A作于N,根据等腰三角形的性质得到,根据全等三角形的性质得到,根据等腰直角三角形的性质即可得到结论.
(1)解:∵四边形是矩形,
∴,,,
∵平分,
∴,
∴是等腰直角三角形,
∴,
∴,
∴;
(2)①,
理由:连接EF,如图所示:
由(1)得:,,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴;
②∵四边形是矩形,
∴,
∴,
过D作于M,
∴,
∴,
∴,
∵,
∴,
由①知,,
∵,
∴,
∴,
∴,
过A作于N,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
由①知,,
∴,,
∴.
【点拨】本题考查了四边形的综合题,矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质等知识;熟练掌握全等三角形的判定与性质、等腰直角三角形的判定与性质是解题的关键.
23.(1)证明见分析 (2)4 (3)
【分析】(1)根据,,是边上的中线,得到,,再结合,得到,即可得到证明;
(2)由可得,即可得到四边形的面积等于面积,根据中线即可得到答案;
(3)由可得 ,,即可得到,在用表示,在即可得到答案.
解:(1)证明:∵,,是边上的中线,
∴ ∠ADC=90°,,,,
∴,
∵,,
∴,
在和中,
,
∴;
(2)解:∵,
∴,
∴
;
(3)解:,理由如下,
∵,
∴ ,,
∵,
∴,
在中根据勾股定理可得,
,
在中,
,
∴.
【点拨】本题考查等腰三角形性质:底边上三线合一;直角三角形性质:斜边中线等于斜边一半;三角形中线性质:分得两个三角形面积相等等于大三角形一半;三角形全等判定与性质及勾股定理.
24.(1)证明见详解 (2)或 (3)或或
【分析】(1)由,可以得到为中点,由于和关于对称,可以得到为中点,由此得到为的中位线,即可证明;
(2)因为点在矩形的对角线,所以点可以落在上,也可以在上,根据题意画出图形,利用垂直平分线的性质,勾股定理,设出参数,列出方程,即可解决;
(3)因为点到矩形一个顶点的距离等于2,所以需要分四类讨论,即顶点分别为,,,,根据题意画出图形,利用勾股定理,面积法等知识即可解决.
(1)证明:如图1,
四边形为矩形,
,
,
,
,
和关于对称,
,
是的中位线,
;
(2)解:①如图2,当点在对角线上时,
和关于对称,
垂直平分,
,,
设,则,
,
,
在中,,
,
,
,
②如图3,当点在对角线上时,
四边形为矩形,
,
,
,
,
设,,
,
①,
,
②,
联立①②得,
,
解得,
,
或;
(3)解:①当点到点距离为2时,
,
此种情况不存在,
②当点到点距离为2时,连接,
则,,
过作于,于,如图4,
,
四边形为矩形,
,
设,则,
,
,
,
,
,
③当点到点距离为2时,如图5,连接,
则,
,
又,,
,
,,三点共线,
即在线段上,
,
;
④当点到点距离为2时,如图6,连接,
则,
,
,
,
,
,
,
即当点到矩形顶点的距离等于2时,的面积为,
当点到矩形顶点的距离等于2时,的面积为,
当点到矩形顶点的距离等于2时,的面积为.
【点拨】本题是一道四边形综合题,考查了轴对称的性质,勾股定理的应用,方程思想,面积法等知识,结合题意,画出合适的图形,是解决本题的突破口,同时要注意分类讨论思想.
1
一、单选题
1.在菱形ABCD中,对角线AC与BD相交于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是 ( )
A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC
2.如图,在矩形ABCD中,点O为对角线BD的中点,过点O作线段EF交AD于F,交BC于E,OB=EB,点G为BD上一点,满足EG⊥FG,若∠DBC=30°,则∠OGE的度数为( )
A.30° B.36° C.37.5° D.45°
3.如图,在矩形中,是延长线上一点,,连接、,过点作于点,为上一点,连接,.若,,则的长为( )
A. B.8 C. D.
4.如图,在矩形中,是边上的动点,于,于,如果,那么( )
A. B.
C. D.
5.把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案,顶点A,D互相重合,中间空白部分是以E为直角顶点,腰长为2cm的等腰直角三角形,则纸片的长AD(单位:cm)为( )
A. B. C. D.
6.如图,中,,,,点D是的中点,将沿翻折得到,连接,,则线段的长等于( )
A. B. C. D.
7.如图,在平面直角坐标系中,已知点A(1,1),B,C,D,把一根长为2022个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点D处,并按D→A→B→C→D…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
A.(1,0) B.(0,1) C. D.
8.如图,矩形纸片中,,,点E、G分别在上,将、分别沿翻折,翻折后点C与点F重合,点B与点P重合.当A、P、F、E四点在同一直线上时,线段长为( )
A. B. C. D.
9.如图.每个小正方形的边长为1,格点线段与交于点,与交于点,连接.有下列结论①;②;③;④;⑤;⑥的面积为0.75.其中正确的结论有( )
A.3个 B.4个 C.5个 D.6个
10.如图,在中,,,斜边的两个端点分别在相互垂直的射线、上滑动,下列结论:①若、两点关于对称,则;②、两点距离的最大值为;③若平分,则;④ 四边形的面积为.其中正确结论的个数是( )
A. B. C. D.
二、填空题
11.如图,已知矩形中,与相交于,平分交于,,则的度数为_______.
12.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则S△ECF的值为____.
13.如图,在矩形ABCD中,,对角线,BE平分∠ABC交AD于点E,Q是线段BE上的点,连接CQ,过点C作CP⊥CQ交AD的延长线于点P,当△PCQ为等腰三角形时,AP=______.
14.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH=_______.
15.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是_____平方厘米.
16.如图,在矩形ABCD中,AB=,BC=1,将△ABD沿射线DB平移得到△A'B'D',连接B′C,D′C,则B'C+D'C的最小值是_____.
17.如图,在矩形中,,对角线,点,分别是线段,上的点,将沿直线折叠,点,分别落在点,处.当点落在折线上,且时,的长为______.
18.在直角梯形中,AD∥BC,,,,那么________.
三、解答题
19.已知:矩形ABCD中,对角线AC与BD交于点O,CE平分,交AB于点E,,求的度数.
20.如图,DE是△ABC的中位线,过点C作CF∥AB,交DE的延长线于点F.
(1) 求证:BC=DF;
(2) 连接CD、AF,当△ABC满足什么条件时,四边形ADCF是矩形,请说明理由.
21.将矩形置于平面直角坐标系中,点A的坐标为,点C的坐标为点,点在BC上,将矩形沿折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当时,求点E的坐标;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
22.如图,在矩形中,平分交于E,连接,.
(1) 如图1,若,,求的长;
(2) 如图2,若点F是边上的一点,若,连结交于G,
①猜想的度数,并说明理由;
②若,求的值.
23.如图,在中,,,是边上的中线,点E,F分别在,边上运动(点E不与点A,C重合),且保持,连接,,.
(1)求证:;
(2)求四边形的面积;
(3)请直接写出三条线段,,之间的数量的关系:_______.
24.如图1,在矩形中,,,点为边上一动点,连接,作点关于直线的对称点,连接,,,,与交于点.
若DE=2,求证:AE//CF.
如图2,连接AC,BD,若点F在矩形ABCD的对角线上,求所有满足条件的DE的长.
如图3,连接BF,当点F到矩形ABCD一个顶点的距离等于2时,请直接写出△BCF的面积.
参考答案
1.A
【分析】根据有一个角是直角的平行四边形是矩形,对角线相等的平行四边形是矩形,对各选项分析判断后利用排除法求解.
解:A、AB=AD,则 ABCD是菱形,不能判定是矩形,故本选项错误;
B、OA=OB,根据平行四边形的对角线互相平分,AC=BD,对角线相等的平行四边形是矩形可得 ABCD是矩形,故本选项正确;
C、AC=BD,根据对角线相等的平行四边形是矩形,故本选项正确;
D、DC⊥BC,则∠BCD=90°,根据有一个角是直角的平行四边形是矩形可得 ABCD是矩形,故本选项正确.
故选:A.
【点拨】此题考察矩形的判定,熟记判定定理才可正确解答.
2.C
【分析】根据矩形和平行线的性质,得;根据等腰三角形和三角形内角和性质,得;根据全等三角形性质,通过证明,得;根据直角三角形斜边中线、等腰三角形、三角形内角和性质,推导得,再根据余角的性质计算,即可得到答案.
解:∵矩形ABCD
∴
∴
∵OB=EB,
∴
∴
∵点O为对角线BD的中点,
∴
和中
∴
∴
∵EG⊥FG,即
∴
∴
∴
故选:C.
【点拨】本题考查了矩形、平行线、全等三角形、等腰三角形、三角形内角和、直角三角形的知识;解题的关键是熟练掌握矩形、全等三角形、等腰三角形、直角三角形斜边中线的性质,从而完成求解.
3.A
【分析】先证得△CDE是等腰直角三角形,再进一步说明∠EBC=∠CGB得到CG=BC=EG=4,说明三角形BCG为等腰三角形,进而说明GH=BH、∠CHB=90°,再根据直角三角形的性质求得CH=BC=2,进而求得GH=BH=CH=2,最后根据EH=GH+GE求解即可.
解:∵四边形ABCD是矩形
∴∠CDA=90°,AD//BC
∴∠CDE=90°,∠AEB=∠EBC=30°
∵ED=CD
∴△CDE是等腰直角三角形
∴∠DCE=∠DEC=45°
∴∠CEB=45°-30°=15°
∵EG=CG
∴∠GCE=∠GEB=15°
∴∠CGB=∠GCE+∠CEB=30°
∴∠EBC=∠CGB
∴CG=BC=4
∴EG=4
∵CH⊥BE
∴GH=BH,∠CHB=90°
∵∠EBC=30°
∴CH=BC=2,GH=BH=CH=2
∴EH=GH+EG=4+2.
故选A.
【点拨】本题主要考查了矩形的性质、等腰三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半等知识点,灵活运用相关知识点成为解答本题的关键.
4.A
【分析】设AC、BD交于点O,连接OP,根据矩形的性质及勾股定理求出OA=OD=2.5,再求出△AOD的面积,根据面积关系即可求出答案.
解:设AC、BD交于点O,连接OP,
∵,
∴BD=AC=5,
∴OA=OD=2.5,
∵,
∴,
∵于,于,
∴,
,
∴,
故选:A.
【点拨】此题考查矩形的性质,勾股定理,根据矩形的性质求出△AOD的面积是解题的关键.
5.D
【分析】如图,过点M作MH⊥A'R于H,过点N作NJ⊥A'W于J.想办法求出AR,RM,MN,NW,WD即可解决问题.
解:如图,过点M作MH⊥A'R于H,过点N作NJ⊥A'W于J.
由题意△EMN是等腰直角三角形,EM=EN=2,MN=
∵四边形EMHK是矩形,
∴EK= A'K=MH=1,KH=EM=2,
∵△RMH是等腰直角三角形,
∴RH=MH=1,RM=,同法可证NW=,
题意AR=R A'= A'W=WD=4,
∴AD=AR+RM+MN+NW+DW=4++++4=.
故答案为:D.
【点拨】本题考查翻折变换,等腰直角三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,构造特殊三角形或特殊四边形解决问题.
6.D
【分析】延长交于点,作,垂足为.首先证明垂直平分线段,是直角三角形,求出的长,在中,利用勾股定理即可解决问题.
解:如图,延长交于点,作,垂足为.
在中,,,
.
为的中点,
.
,
,
解得.
由翻折的性质可知,,
,
.
,,
.
.
根据折叠的性质有:,
,
,,
又,,
,
为直角三角形.
.
故选:D.
【点拨】本题考查翻折变换、直角三角形的斜边中线的性质、勾股定理等知识,解题的关键是学会利用面积法求高,属于中考常考题型.
7.A
【分析】先求出四边形ABCD的周长为10,得到2022÷10的余数为2,由此即可解决问题.
解:∵A(1,1),B(1,1),C(1,2),D(1,2),
∴AB∥x轴,CD∥x轴,AD∥y轴,BC∥y轴,
∴AB⊥AD,AB⊥BC,CD⊥AB,CD⊥BC,
∴∠A=∠B=∠C=∠D=90°,
∴四边形ABCD是矩形,
∵AB=1-(-1)=2,BC=1-(-2)=3,
∴四边形ABCD的周长为:2(AB+BC)=10,
∵2022÷10=202…2,且AD=3,
∴细线另一端所在位置的点在D处上面2个单位的位置,坐标为(1,0).
故选:A.
【点拨】本题主要考查了规律型:点的坐标,解决问题的关键是熟练掌握矩形的周长公式,运用除法得到的余数确定点的位置.
8.B
【分析】根据矩形的性质得到,,,根据折叠的性质得到,,,根据勾股定理得到,设,由勾股定理列方程得到,由折叠的性质得到,,,求得,设,则,根据勾股定理列方程即可得到结论.
解:在矩形纸片中,,,
∴,,,
∵将沿翻折,翻折后点C与点F重合,
∴,,,
∴,
设,
∴,,
∵,
∴,
解得:,
∴,
∵将沿翻折,翻折后点B与点P重合,
∴,,,
∴,
设,
则,
∵,
∴,
∴,
∴线段GP长为,
故选:B.
【点拨】本题考查了翻折变换(折叠问题),矩形的性质,勾股定理,根据勾股定理列方程是解题的关键.
9.B
【分析】先证明,再逐个选项推理即可.
解:如图,
由图可得,,
∴,
∴
∵,
∴,
∴,
∴,故①正确;
∵,
∴
∴
∴,
∴,
∴,故②正确;
∵中,
∴,
∴,故③错误;
∵,,
∴,故④错误;
连接,
∵
∴,
∵,
∴,
∵,
∴
∴,故⑤正确;
∵矩形,
∴,
∵,
∴,
∴的面积为0.75,故⑥正确;
综上所述,正确的有①②⑤⑥;
故选:B.
【点拨】本题考查了全等三角形的性质与判定,矩形的性质,掌握这些性质是解决问题的关键.
10.B
解:在中,,,∴,,∴若、两点关于对称,如图,∴为的垂直平分线,∴,∴①正确;
②如图,取的中点为,连接、.
∵,∴.
当经过点时,最大且、两点距离的最大值为,∴②正确;
③如图,当,,∴四边形是矩形,∴与相互平分,但与的夹角为、,不垂直,∴③不正确;
④如图,此时四边形的面积,,∴④不正确.
综上所述:正确的有①②,个结论.故选.
点睛:本题是三角形的综合题,熟练掌握直角三角形斜边中线等于斜边一半是解答本题的关键,难度适中.
11.
【分析】先求出∠ADB,再说明三角形ODC是等边三角形,推出CD=OC,CE=CD,求出CE=OC,求出∠COE=∠OEC和∠OCB=30°即可解答.
解:∵四边形ABCD是矩形,
∴AD//BC,∠ADC=90°,OA=OC,OB=OD,AC=BD,
∵DE平分∠ADC,
∴∠ADE=∠CDE=∠ADC=45°,
∵∠BDE=15°,
∴∠ADB=∠ADE-∠BDE=30°,
∵AD∥BC,
∴∠ADB=∠DBC=30°,
∴OA=OD=OB=OC,
∴∠OBC=∠OCB=30°,
∴∠DOC=∠OBC+∠OCB=60°,
∵OD=OC,
∴△ODC是等边三角形,
∴DC=OC,
∵AD∥BC,
∴∠ADE=∠DEC
∴∠ADE=∠CDE,
∴∠DEC=∠CDE,
∴CE=DC
∴CE=OC,
∴∠COE=∠OEC,
∵∠OCB=30°,
∴∠COE=(180°-∠OCE)=75°.
故答案为75°.
【点拨】本题考查了矩形的性质、、等边三角形的性质和判定、三角形的内角和定理等知识点,灵活应用所学知识是解答本题的关键.
12.
【分析】连接BF,根据三角形的面积公式求出BH,得到BF,根据直角三角形的判定得到∠BFC=90°,再根据勾股定理求出CF的长度,进而即可求出S△ECF.
解:如图,连接BF,
,
∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE=,
由折叠可知:BF⊥AE(对应点的连线必垂直于对称轴),
∴BH=,
∴BF=,
∵EF=BE=CE,
∴∠BFC=90°,
根据勾股定理可得:CF=,
S△ECF=S△BCF=×××=,
故答案为:.
【点拨】本题考查矩形的性质,折叠的性质,勾股定理以及三角形的面积公式,掌握知识点是解题关键.
13.5
【分析】过点Q作于点H,由矩形的性质并结合勾股定理确定,再证明以及为等腰三角形,即可推导,,然后由计算AP的长即可.
解:过点Q作于点H,如下图,
∵四边形ABCD为矩形,
∴,,,
∵,,
∴,
∵,点P在AD的延长线上,
∴,
∵△PCQ为等腰三角形,CP⊥CQ,
∴,,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∵BE平分∠ABC,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴.
故答案为:5.
【点拨】本题主要考查了矩形的性质、全等三角形的判定与性质、勾股定理以及等腰三角形的判定与性质等知识,正确作出辅助线,构建全等三角形是解题的关键.
14.
【分析】延长GH交AD于M点,由矩形的性质得出CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,推出DG=CG-CD=2,∠HAM=∠HFG,由ASA证得△AMH≌△FGH,得出AM=FG=1,MH=GH,则MD=AD-AM=2,在Rt△MDG中,根据勾股定理得到GM,即可得出结果.
解:延长GH交AD于M点,如图所示:
∵四边形ABCD与四边形CEFG都是矩形,
∴CD=CE=FG=1,BC=EF=CG=3,BE∥AD∥FG,
∴DG=CGCD=3-1=2,∠HAM=∠HFG,
∵AF的中点H,
∴AH=FH,
在△AMH和△FGH中,
,
∴△AMH≌△FGH(ASA).
∴AM=FG=1,MH=GH,
∴MD=AD-AM=31=2,
在Rt△MDG中,GM=,
∴GH=GM=,
故答案为:.
【点拨】本题考查了矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握矩形的性质,证明三角形全等是解题的关键.
15.48
【分析】如下图,设矩形ABCD的长为m,宽为n,过点F作BC、DC的垂线,利用m、n表示出△BFD的面积,从而得出mn的大小,进而得出矩形ABCD的面积.
解:如下图,过点F作BC、CD的垂线,分别交于点Q、G,设矩形ABCD的长为m,宽为n
∵点E是AD的中点,点F是EC的中点,AD=m,AB=n
∴FQ=,FG==
∴
∴mn=48
故答案为:48
【点拨】本题考查三角形面积问题,解题关键是利用表示出△BFD的面积,从而推导出mn的大小.
16.
【分析】根据矩形的性质和勾股定理可得BD=2,即为B′D′的长,作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,则有CD′=GD′,CE⊥BD,CG=2CE,利用三角形的面积可求得CG=,然后以B′D′,GD′为邻边作平行四边形B′D′GH,可得B′H=D′G=CD′,于是当C,B′,H在同一条直线上时,CB′+B′H最短,且B'C+D'C的最小值=CH,再根据勾股定理即可求出结果.
解:∵四边形ABCD是矩形,
∴AD=BC=1,∠A=90°,
∴,
∵将△ABD沿射线DB平移得到△A'B'D',
∴B′D′=BD=2,
作点C关于BD的对称点G,连接CG交BD于E,连接D′G,如图,
则CD′=GD′,CE⊥BD,CG=2CE,
∵CE=,∴CG=,
以B′D′,GD′为邻边作平行四边形B′D′GH,
则B′H=D′G=CD′,
∴当C,B′,H在同一条直线上时,CB′+B′H最短,
则B'C+D'C的最小值=CH,
∵四边形B′D′GH是平行四边形,
∴HG=B′D′=2,HG∥B′D′,
∴HG⊥CG,
∴CH=.
故答案为:.
【点拨】本题考查了矩形的性质、轴对称的性质、平移的性质、平行四边形的性质和勾股定理等知识,具有一定的难度,利用轴对称和平移的思想把所求B'C+D'C的最小值转化为求CB′+B′H的最小值是解题的关键.
17.2或
【分析】分两种情况讨论,由折叠的性质和勾股定理可求解.
解:,,
,
当点落在上时,
将沿直线折叠,
,
,
,
;
当点落在上时,如图2,连接,过点作于,
,
,
,
,
,
将沿直线折叠,
,
,
,
,
综上所述:的长为2或.
【点拨】本题考查了矩形的性质,折叠的性质,勾股定理等知识,利用勾股定理列出方程是解题的关键.
18.或##或
【分析】该题根据题意分为两种情况,首先正确画出图形,根据已知易得的直角边和斜边的长,然后利用直角三角形斜边中线等于斜边一半得到等边三角形,进而即可求解.
解:∠C存在两种情况:
①当为锐角时,如图,过作,垂足为,取的中点,连接,
,,
,
,
四边形是矩形,
,
,
,
∵,,
∴,
∴,
∴;
②当为钝角时,如图,过作,垂足为,取的中点,连接,
同理①可得,
又∵,
.
∴
综上,或,
故答案为或.
【点拨】该题重点考查了直角三角形的性质和等边三角形判定和性质,解决该题的关键一是:能根据题意画出两种情况,二是:把该题转化为直角三角形问题,从而即可求解.
19.75°
【分析】根据矩形的性质及CE平分得到∠BEC=∠BCE=∠DCE=45°,得到BE=BC,利用由此得到∠BAC=30°,根据矩形的性质证得△OBC是等边三角形,得到BC=OB=BE,由∠EBO=∠BAC=30°求出答案.
解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,OA=OB=OC=OD,CD∥AB,
∵CE平分,
∴∠BCE=∠DCE=45°,
∵CD∥AB,
∴∠BEC=∠BCE=∠DCE=45°,
∴BC=BE,
∵,
∴∠BAC=30°,
∴∠ACB=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OB=BE,
∵∠EBO=∠BAC=30°,
∴∠BEO=,
故答案为:75°.
【点拨】此题考查矩形的性质,等边三角形的判定及性质,等腰三角形等边对等角的性质,角平分线的性质,题中证得BE=OB是解题的关键.
20.(1)见分析 (2)当BC=AC时,四边形ADCF是矩形,理由见分析.
【分析】(1)用平行四边形的定义判定;
(2)当BC=AC时,四边形ADCF是矩形.用DE是三角形中位线证明BD=AD,用四边形DBCF是平行四边形得到CF∥BD,CF=BD,得到AD=CF,推出四边形ADCF是平行四边形,根据AC=BC,BC=DF,得到AC=DF,从而平行四边形ADCF是矩形.
解:(1)∵DE是△ABC的中位线,
∴2DE=BC,DE∥BC,
∵CF∥AB,
∴四边形DBCF是平行四边形,
∴BC=DF;
(2)当BC=AC时,四边形ADCF是矩形,理由如下:
∵DE是△ABC的中位线,
∴DB=AD,
∵四边形DBCF是平行四边形,
∴DB=CF,
∴AD=CF,
∵AB∥CF,
∴四边形ADCF是平行四边形,
∵BC=AC,BC=CF,
∴AC=DF,
∴平行四边形ADCF是矩形.
【点拨】本题主要考查了三角形中位线,平行四边形,熟练掌上三角形中位线性质,平行四边形的判定和性质,是解决此类问题的关键.
21.(1). (2)点E能恰好落在x轴上.
【分析】(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标;
(2)由折叠的性质求得线段和的长,然后利用勾股定理得到有关m的方程,求得m的值即可.
解:(1)当时,点B的坐标为,
∴,
∴是等腰直角三角形,
∴,则,
∴,
则E在y轴上,且,
∴,则点E的坐标为.
(2)点E能恰好落在x轴上.
理由如下:
∵四边形为矩形,
∴,,
由折叠的性质可得:,.
假设点E恰好落在x轴上,则,
即,
则.
在中,即,
即,解得.
【点拨】本题考查了翻折变换的性质、矩形的性质、勾股定理、坐标与图形性质、等腰直角三角形的判定与性质等知识;熟练掌握翻折变换的性质和勾股定理是解题的关键.
22.(1) (2)①,理由见分析;②
【分析】(1)由矩形的性质得,,,由角平分线的性质得出,则是等腰直角三角形,得出,推出,由勾股定理得出;
(2)①连接,由(1)得,,由证得,得出,,证明是等腰直角三角形,即可得出结论;
②根据矩形的性质得到,求得,过D作于M,根据余角的性质得到,得到,过A作于N,根据等腰三角形的性质得到,根据全等三角形的性质得到,根据等腰直角三角形的性质即可得到结论.
(1)解:∵四边形是矩形,
∴,,,
∵平分,
∴,
∴是等腰直角三角形,
∴,
∴,
∴;
(2)①,
理由:连接EF,如图所示:
由(1)得:,,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴是等腰直角三角形,
∴;
②∵四边形是矩形,
∴,
∴,
过D作于M,
∴,
∴,
∴,
∵,
∴,
由①知,,
∵,
∴,
∴,
∴,
过A作于N,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
由①知,,
∴,,
∴.
【点拨】本题考查了四边形的综合题,矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质等知识;熟练掌握全等三角形的判定与性质、等腰直角三角形的判定与性质是解题的关键.
23.(1)证明见分析 (2)4 (3)
【分析】(1)根据,,是边上的中线,得到,,再结合,得到,即可得到证明;
(2)由可得,即可得到四边形的面积等于面积,根据中线即可得到答案;
(3)由可得 ,,即可得到,在用表示,在即可得到答案.
解:(1)证明:∵,,是边上的中线,
∴ ∠ADC=90°,,,,
∴,
∵,,
∴,
在和中,
,
∴;
(2)解:∵,
∴,
∴
;
(3)解:,理由如下,
∵,
∴ ,,
∵,
∴,
在中根据勾股定理可得,
,
在中,
,
∴.
【点拨】本题考查等腰三角形性质:底边上三线合一;直角三角形性质:斜边中线等于斜边一半;三角形中线性质:分得两个三角形面积相等等于大三角形一半;三角形全等判定与性质及勾股定理.
24.(1)证明见详解 (2)或 (3)或或
【分析】(1)由,可以得到为中点,由于和关于对称,可以得到为中点,由此得到为的中位线,即可证明;
(2)因为点在矩形的对角线,所以点可以落在上,也可以在上,根据题意画出图形,利用垂直平分线的性质,勾股定理,设出参数,列出方程,即可解决;
(3)因为点到矩形一个顶点的距离等于2,所以需要分四类讨论,即顶点分别为,,,,根据题意画出图形,利用勾股定理,面积法等知识即可解决.
(1)证明:如图1,
四边形为矩形,
,
,
,
,
和关于对称,
,
是的中位线,
;
(2)解:①如图2,当点在对角线上时,
和关于对称,
垂直平分,
,,
设,则,
,
,
在中,,
,
,
,
②如图3,当点在对角线上时,
四边形为矩形,
,
,
,
,
设,,
,
①,
,
②,
联立①②得,
,
解得,
,
或;
(3)解:①当点到点距离为2时,
,
此种情况不存在,
②当点到点距离为2时,连接,
则,,
过作于,于,如图4,
,
四边形为矩形,
,
设,则,
,
,
,
,
,
③当点到点距离为2时,如图5,连接,
则,
,
又,,
,
,,三点共线,
即在线段上,
,
;
④当点到点距离为2时,如图6,连接,
则,
,
,
,
,
,
,
即当点到矩形顶点的距离等于2时,的面积为,
当点到矩形顶点的距离等于2时,的面积为,
当点到矩形顶点的距离等于2时,的面积为.
【点拨】本题是一道四边形综合题,考查了轴对称的性质,勾股定理的应用,方程思想,面积法等知识,结合题意,画出合适的图形,是解决本题的突破口,同时要注意分类讨论思想.
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
