4.3物质的密度(2)

课件32张PPT。第四章 物质的特性4.3　物质的密度(2) 1. 能根据密度的定义式推导出其变形公式。
2. 了解密度的定义式及其变形公式的应用。课前 · 预学区自主学习　基础落实 学习目标知识清单尝试练习课前 · 预学区自主学习　基础落实 学习目标尝试练习1. 密度的定义式：ρ＝m/V，变形公式：　　　　　　、
　　　　　　　　。
2. 密度公式的应用：
(1)利用公式ρ＝m/V求出物质的密度，再对照密度表
就可以鉴别物质。还可以用于鉴别物质是否纯净，
物体是否空心等。
(2)由公式m＝ρV可知，通过测量体积可以求出不便直
接测量的物体的质量。
(3)由公式V＝m/ρ可知，通过测量质量可以求出不便
直接测量的物体的体积。　V＝m/ρ m＝ρV知识清单课前 · 预学区自主学习　基础落实 学习目标尝试练习1. 三个体积相等、质量相等的空心球，分别由铜、铁、
铝制成（ρ铜＞ρ铁＞ρ铅），其内部空心体积最大的
是 （　　）　　　　
A. 铜球 B. 铁球
C. 铅球 D. 无法确定A　知识清单课前 · 预学区自主学习　基础落实 学习目标尝试练习2. 甲、乙两种材料制成的实心物体，已知甲的密度是乙
的2倍,甲的体积是乙的1/4,则它们的质量之比m甲∶m乙
是 （　　）
A. 1∶8 B. 8∶1
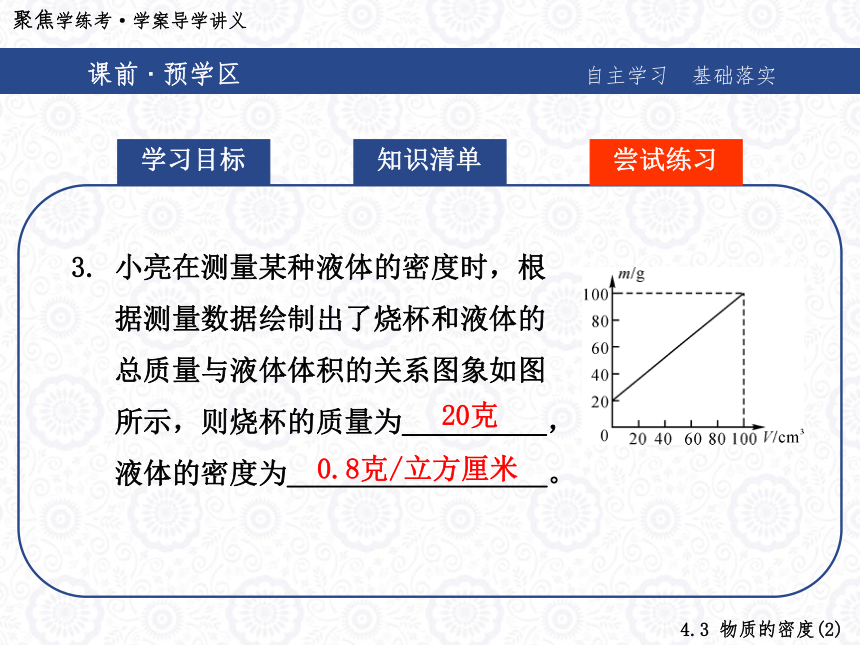
C. 1∶2 D. 2∶1C　知识清单课前 · 预学区自主学习　基础落实 学习目标尝试练习3. 小亮在测量某种液体的密度时，根
据测量数据绘制出了烧杯和液体的
总质量与液体体积的关系图象如图
所示，则烧杯的质量为__________，
液体的密度为__________________。 20克　0.8克/立方厘米知识清单典例 · 精析区 以题说法　互动探究 解 析跟踪训练【例1】　甲、乙两种物质的质量与体积关系如图所示，由
图可知 （　　）
A. ρ甲＞ρ乙
B. ρ甲＜ρ乙
C. 若V甲＝V乙，则m甲＜m乙
D. 若m甲＝m乙，则V甲＞V乙典例 · 精析区 以题说法　互动探究 解析　本题考查根据图象判断密度。由图可求出ρ甲＝
2克/立方厘米，ρ乙＝0.5克/立方厘米，则ρ甲＞ρ乙；
体积相同时，密度大的物质质量也大，即m甲＞m乙；质
量相同时，密度大的物质体积小，即V甲＜V乙。典例 · 精析区 以题说法　互动探究 【例1】　甲、乙两种物质的质量与体积关系如图所示，由
图可知 （　　）
A. ρ甲＞ρ乙
B. ρ甲＜ρ乙
C. 若V甲＝V乙，则m甲＜m乙
D. 若m甲＝m乙，则V甲＞V乙A　 解 析跟踪训练跟踪训练1　甲、乙、丙三种物质的质量与体积的关系如
图所示，ρ甲、ρ乙、ρ丙、ρ水分别代表甲、乙、丙
三种物质和水的密度。据图可知 （　　）
A. ρ甲＞ρ乙＞ρ丙，且ρ丙＞ρ水
B. ρ甲＞ρ乙＞ρ丙，且ρ甲＞ρ水
C. ρ甲＜ρ乙＜ρ丙，且ρ丙＝ρ水
D. ρ甲＜ρ乙＜ρ丙，且ρ甲＞ρ水典例 · 精析区 以题说法　互动探究 B　 典例 · 精析区 以题说法　互动探究 解 析跟踪训练【例2】　质量为100克,容积为400立方厘米的玻璃瓶,当装
满某种油时称得其总质量是420克,请通过计算说明瓶中
装的是何种油？(ρ植物油＝0.9×103千克/立方米,ρ煤油＝
0.8×103千克/立方米,ρ汽油＝0.71×103千克/立方米) 典例 · 精析区 以题说法　互动探究 本题只要计算出物质的密度，便可利用密度鉴
别物质。求解本题关键是准确地找出瓶中油的
质量(m油)。计算密度时注意单位要统一。 【例2】　质量为100克,容积为400立方厘米的玻璃瓶,当装
满某种油时称得其总质量是420克,请通过计算说明瓶中
装的是何种油？(ρ植物油＝0.9×103千克/立方米,ρ煤油＝
0.8×103千克/立方米,ρ汽油＝0.71×103千克/立方米) 解 析跟踪训练典例 · 精析区 以题说法　互动探究 【例2】　质量为100克,容积为400立方厘米的玻璃瓶,当装
满某种油时称得其总质量是420克,请通过计算说明瓶中
装的是何种油？(ρ植物油＝0.9×103千克/立方米,ρ煤油＝
0.8×103千克/立方米,ρ汽油＝0.71×103千克/立方米) 解：m油＝420克－100克＝320克＝0.32千克,
V油＝400立方厘米＝4×10－4立方米,
ρ油＝m油/V油＝ 0.32千克/4×10－4立方米
＝0.8×103千克/立方米,
根据油的密度可以确定它是煤油。解 析跟踪训练跟踪训练2　小明在学校运动会上获得一块奖牌，他想知道
这块奖牌是否由纯铜制成，于是他用天平和量杯分别测
出该奖牌的质量和体积为14g和2cm3，并算出它的密度为　　　　
g/cm3。小明通过查密度表知道，铜的密度为
8.9×103kg/m3，由此他判断该奖牌　　　　　由纯铜制
成的（选填“是”或“不是”）。典例 · 精析区 以题说法　互动探究 不是7　随堂 · 检测区 即时演练　查漏补缺 A. 基础过关 1. 甲、乙、丙三个物体的密度分别为ρ1＝2.7吨/米3，
ρ2＝2.7千克/分米3，ρ3＝2.7克/厘米3，则三者中
密度是 （　　）
A. 甲最大 B. 乙最大
C. 丙最大 D. 一样大 D　随堂 · 检测区 即时演练　查漏补缺 2. 根据如图所提供的信息，可知木块的密度是 （　　）
A. 0.6克/厘米3
B. 0.5克/厘米3
C. 5克/厘米3
D. 6克/厘米3A　随堂 · 检测区 即时演练　查漏补缺 3. 人的密度跟水的密度差不多，请你估算一个中学生的
体积最接近下列哪一个值 （　　）
A. 50立方米 B. 50立方分米
C. 50立方厘米 D. 50立方毫米B　随堂 · 检测区 即时演练　查漏补缺 4. 已知ρ酒精＝0.8×103千克/米3,ρ柴油＝0.85×103千克/
米3,ρ汽油＝0.71×103千克/米3,ρ硫酸＝1.8×103千克/
米3,一个最多能装下1千克水的瓶子,能装下1千克的
（　　）
A. 酒精 B. 汽油
C. 柴油 D. 硫酸D　随堂 · 检测区 即时演练　查漏补缺 5. 一个质量为890克的铜球，测出它的体积为120厘米3，
则此铜球为（ρ铜＝8.9×103千克/米3） （　　）
A. 一定是空心铜球
B. 一定是实心铜球
C. 可能是空心铜球，可能是实心铜球
D. 无法确定A　随堂 · 检测区 即时演练　查漏补缺 6. 中间空心的铁球、木球、铝球、铅球,质量和体积都相
等，中空部分最大的是(ρ铅＞ρ铁＞ρ铝＞ρ木)(　　)
A. 铁球 B. 木球
C. 铅球 D. 铝球C　随堂 · 检测区 即时演练　查漏补缺 7. 甲、乙两个均匀的实心正方体,它们的边长之比为1∶2，
质量之比是1∶2，则它们的密度之比是 （　　）
A. 1∶2 B. 2∶1
C. 1∶4 D. 4∶1D　随堂 · 检测区 即时演练　查漏补缺 8. 一个质量为0.25 kg的玻璃瓶，盛满水时称得质量是
1.5kg，若盛满某液体时称得质量1.75kg，那么这种
液体的密度是 （　　）
A. 1.0×103kg/m3 B. 1.16×103kg/m3
C. 1.2×103kg/m3 D. 1.75×103kg/m3C　随堂 · 检测区 即时演练　查漏补缺 9. 下列判断正确的是 （　　）
A. 最多装500克酒精的容器，一定能装500克的水
B. 最多装500克水的容器，一定能装500克的酒精
C. 最多装500毫升酒精的容器，一定能装500克的酒精
D. 最多装500毫升水的容器，一定能装500克的酒精A　随堂 · 检测区 即时演练　查漏补缺 10. 能装0.5kg水的瓶子，最多能装密度为0.8×103kg/m3
的煤油　　　　kg。
11. 市场上出售一种“金龙鱼”牌食用调和油，瓶上标有
“5L”字样,已知瓶内调和油的密度为0.92×103kg/m3,
则该瓶油的质量是　　　　kg。如果调和油用去一半,
则剩余半瓶调和油的密度为　 　　　　　　　。0.4　4.6　0.92×103千克/米3　随堂 · 检测区 即时演练　查漏补缺 12. 根据木块m－V关系图象，回答下列问题：
(1)体积是4厘米3的木块质量是　　　　克。
(2)木块的密度是　　　　千克/米3。2　500　随堂 · 检测区 即时演练　查漏补缺 B. 能力提升13. 有一个装满水的瓶,瓶和水的质量一共是500克,现将
16克的小金属块放入瓶内,称得三者的质量为510克，
则这小金属块是 （　　）
A. 铝块 B. 铁块
C. 铜块 D. 银块A　随堂 · 检测区 即时演练　查漏补缺 14. 飞机制造师为了减轻飞机的重量，将钢制零件改为
铝制零件,使其质量减少104千克，则所需铝的质量
是(已知钢的密度是7.9×103千克/米3，铝的密度是
2.7×103千克/米3) （　　）
A. 35.5千克 B. 54千克
C. 104千克 D. 158千克B　随堂 · 检测区 即时演练　查漏补缺 15. 两种液体的密度分别为ρ1、ρ2,若混合前它们的
质量相等，将它们混合后，则混合液体的密度为
；若混合前它们的体积
相等,将它们混合后,则混合液体的密度为
。(设混合前后液体的体积不变)2ρ1ρ2/(ρ1＋ρ2)(ρ1＋ρ2)/2　随堂 · 检测区 即时演练　查漏补缺 16. 盐水选种是我国古代劳动人民发明的一种挑选种子
的方法。在选稻种时需用密度为1.1×103千克/米3
的盐水选种子。现配制了500毫升的盐水，称得它
的质量是0.6千克，这样的盐水是否符合要求？如
果不符合要求，应加盐还是加水？不符合, 应加水。课外 · 拓展区 科学广角　超越自我 冬天一场大雪后地面上出现一层厚厚的积雪，某同学
设计了“根据雪地上的脚印深度进行粗略测量积雪的密度”
的方法。他采用的方法是：利用一块平整地面上的积雪，
用脚竖直向下踩在雪上，形成一个向下凹的脚印，脚踩在
雪上后雪变成冰，冰的密度为已知值ρ冰；然后通过测量
积雪原来的厚度H，用脚踩后在雪上形成脚印的深度h，就
可以估测雪的密度。请通过推导得出雪的密度的计算表达
式。 课外 · 拓展区 科学广角　超越自我 提示：积雪压扁后，变成的冰的质量与雪的质量相等，
根据密度公式比较雪和冰的密度大小关系。
设脚印面积为S，知道积雪原来的厚度，可求雪的体积；
知道用脚踩后在雪上形成脚印的深度，可求冰的厚度，
可求冰的体积，根据质量相等求雪的密度。课外 · 拓展区 科学广角　超越自我 解：雪挤压后，质量不变，体积变小，实验时测得积雪原
来的厚度H，用脚踩后在雪上形成脚印的深度h，冰的密度
为ρ冰；设脚印面积为S，
雪的体积：V雪＝SH，冰的体积：V冰＝(H－h)S，
∵ρ＝ m/ V，雪压成冰质量不变，
∴m雪＝m冰，即ρ雪SH＝ρ冰S(H－h)，
雪的密度：ρ雪＝(H－h)ρ冰/H