重庆市南开中学2013-2014学年高二上学期期末考试数学(文)试题
文档属性
| 名称 | 重庆市南开中学2013-2014学年高二上学期期末考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-27 18:50:59 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
重庆南开中学高2015级高二(上)期末测试
数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题(每小题5分,1O小题,共50分,每小题只有一个选项符合要求)
1.已知,则的值为( )
A. B. C. D.
2.已知命题,命题,则命题p是命题q的( >
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若命题,则对命题p的否定是( )
A.
B.
C.
D.
4.设l、m是两条不同的直线,是两个不同的平面,则下列正确的是( )
A.若l // m,m //,则l // B.若l //,⊥,则l ⊥
C.若l ⊥,l ⊥,则 D.若⊥,∩ = l,l ⊥ m,则m ⊥
5.双曲线的焦点为椭圆的焦点,且椭圆的短轴长为,则该椭
圆的标准方程为( )
A. B. C.
6.函数的最小值为( )
A. -1 B. 0 C.2 D.4
7.已知F是抛物线的焦点,P是抛物线C上一点,若抛物线C在点P处的切线的
倾斜角为,则|PF|=()
A. B. C.4 D.621世纪教育网
8.已知函数y=f(x)是定义在R上的可导函数,且对不等式:恒成
立,若,b,,则a、b、c的大小关系是( )
A. a>c>b B. c>a>b C. a>b>c D. c>b>a
9.长方体ABCD - A1B1C1D1中,A1C与平面AB1D1、平面C1BD交于
E,F两点,点P为线段BC1上一动点,给出下列命题:
(1)点E,F为线段A1C的两个三等分点;(2)点E为△AB1D1的垂心;
(3)三棱锥A-D1PC体积不变;(4) DP⊥BC1
其中真命题为( )
A. (2)(3) B. (1)(3) C. (1)(3)(4) D. (1)(2)
10.已知函数,若函数F(x)=f(x) - kx在区间[]上恰好有一
个零点,则实数k的取值范围为( )
A. (]∪{0} B.[)∪{0}
C.()∪{0} D.(]∪{0}
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题5个小题,每小题5分,共25分)各题答案必须填写在答题卡Ⅱ上相
应位置(只填结果,不写过程).
11.己知球O的表面积为l6,则球O的体积为___ _.
12.曲线y=ex+2x在点(0,1)处的切线方程为___ _.
13.一个几何体的三视图如右图所示,主视图与俯视图21世纪教育网
是全等的矩形,侧视图为圆心角为直角的扇形,部分
边长如图所示,则此几何体的体积为___ _.
14.已知椭圆,斜率为k(k≠0)且不过原点的直线l交椭圆于A,B两点,线段AB
的中点为C,直线OC交椭圆左准线为点D(x0,y0),则x02 +y02 +k2的最小值为___ _.
15.双曲线的两条渐近线分别为l1,l2,右焦点为F,在双曲线右支上存在一点P,
设点P到l1的距离为d1,点P到l2的距离为d2,若d1、、 d d2依次成等比数列,则
该双曲线的离心率e的取值范围是___ _.
三、解答题:(本大题6个小题,共75分)备题解答必须答在答题卡Ⅱ上(必须写出必要的
文字说明、演算步骤或推理过程)
16.(本小题满分13分)
已知命题p:关于x的不等式对任意x∈R恒成立;命题q:函数
上是增函数,若“p∨q留”为真命题,
“p∧q”为假命题,求实数a的取值范围.
17.(本小题满分13分)21世纪教育网
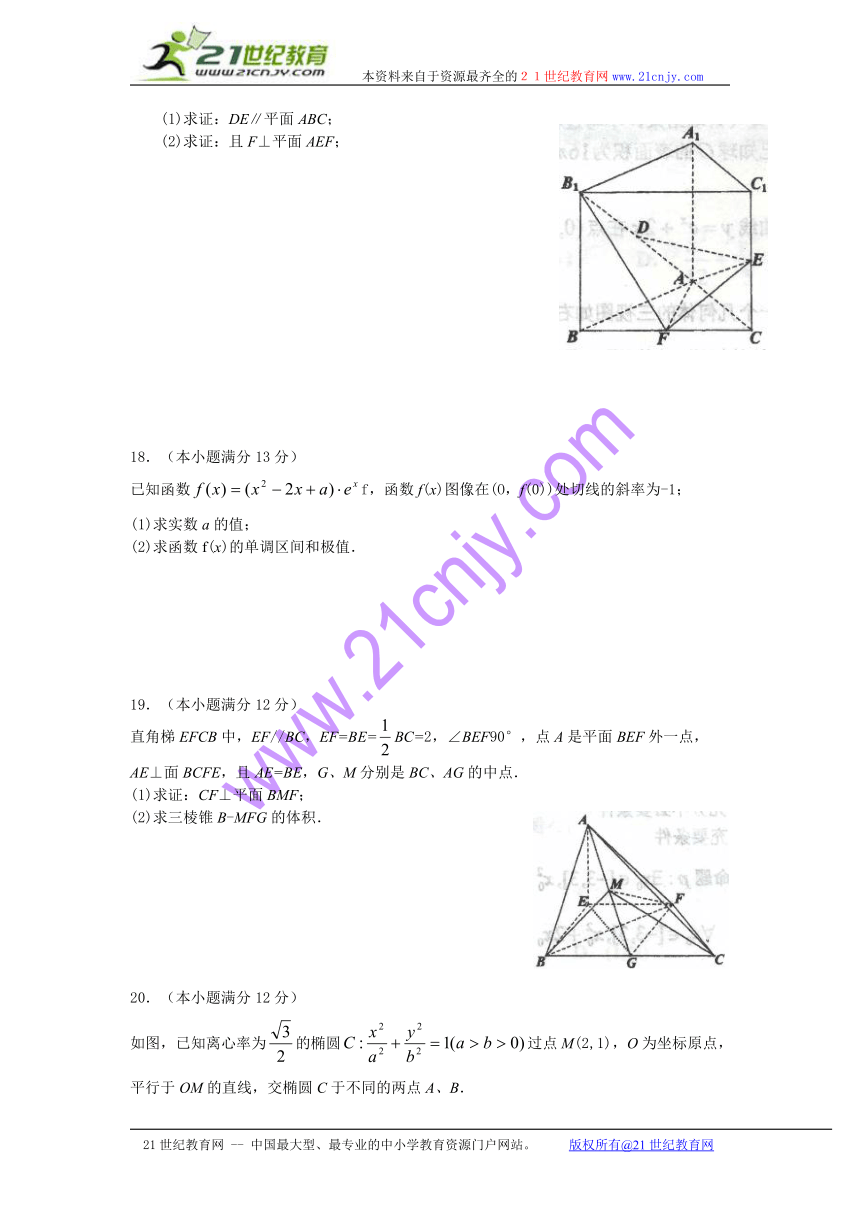
已知直三棱柱ABC –A1B1C1中,△ABC为等腰直角三角形,
∠BAC= 90°,且AB= AA1, D、E、F分别为B1A、C1C、BC的中点.
(1)求证:DE∥平面ABC;
(2)求证:且F⊥平面AEF;
18.(本小题满分13分)
已知函数f,函数f(x)图像在(O,f(0))处切线的斜率为-1;21世纪教育网
(1)求实数a的值;
(2)求函数f(x)的单调区间和极值.
19.(本小题满分12分)
直角梯EFCB中,EF//BC,EF=BE=BC=2,∠BEF90°,点A是平面BEF外一点,
AE⊥面BCFE,且AE=BE,G、M分别是BC、AG的中点.
(1)求证:CF⊥平面BMF;
(2)求三棱锥B-MFG的体积.
20.(本小题满分12分)
如图,已知离心率为的椭圆过点M(2,1),O为坐标原点,
平行于OM的直线,交椭圆C于不同的两点A、B.
(1)求椭圆C的方程;21世纪教育网
(2)记直线MB、MA与x轴的交点P、Q,
证明:△MPQ为等腰三角形
21.(本小题满分12分)
已知,函数.
(1)若函数f(x)在x=2处取得极值,求实数a的值。
(2)设函数g(x)=f(x)-2ax,若方程g(x)=0有唯一解,求实数a的值.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
重庆南开中学高2015级高二(上)期末测试
数学试题(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题(每小题5分,1O小题,共50分,每小题只有一个选项符合要求)
1.已知,则的值为( )
A. B. C. D.
2.已知命题,命题,则命题p是命题q的( >
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.若命题,则对命题p的否定是( )
A.
B.
C.
D.
4.设l、m是两条不同的直线,是两个不同的平面,则下列正确的是( )
A.若l // m,m //,则l // B.若l //,⊥,则l ⊥
C.若l ⊥,l ⊥,则 D.若⊥,∩ = l,l ⊥ m,则m ⊥
5.双曲线的焦点为椭圆的焦点,且椭圆的短轴长为,则该椭
圆的标准方程为( )
A. B. C.
6.函数的最小值为( )
A. -1 B. 0 C.2 D.4
7.已知F是抛物线的焦点,P是抛物线C上一点,若抛物线C在点P处的切线的
倾斜角为,则|PF|=()
A. B. C.4 D.621世纪教育网
8.已知函数y=f(x)是定义在R上的可导函数,且对不等式:恒成
立,若,b,,则a、b、c的大小关系是( )
A. a>c>b B. c>a>b C. a>b>c D. c>b>a
9.长方体ABCD - A1B1C1D1中,A1C与平面AB1D1、平面C1BD交于
E,F两点,点P为线段BC1上一动点,给出下列命题:
(1)点E,F为线段A1C的两个三等分点;(2)点E为△AB1D1的垂心;
(3)三棱锥A-D1PC体积不变;(4) DP⊥BC1
其中真命题为( )
A. (2)(3) B. (1)(3) C. (1)(3)(4) D. (1)(2)
10.已知函数,若函数F(x)=f(x) - kx在区间[]上恰好有一
个零点,则实数k的取值范围为( )
A. (]∪{0} B.[)∪{0}
C.()∪{0} D.(]∪{0}
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题5个小题,每小题5分,共25分)各题答案必须填写在答题卡Ⅱ上相
应位置(只填结果,不写过程).
11.己知球O的表面积为l6,则球O的体积为___ _.
12.曲线y=ex+2x在点(0,1)处的切线方程为___ _.
13.一个几何体的三视图如右图所示,主视图与俯视图21世纪教育网
是全等的矩形,侧视图为圆心角为直角的扇形,部分
边长如图所示,则此几何体的体积为___ _.
14.已知椭圆,斜率为k(k≠0)且不过原点的直线l交椭圆于A,B两点,线段AB
的中点为C,直线OC交椭圆左准线为点D(x0,y0),则x02 +y02 +k2的最小值为___ _.
15.双曲线的两条渐近线分别为l1,l2,右焦点为F,在双曲线右支上存在一点P,
设点P到l1的距离为d1,点P到l2的距离为d2,若d1、、 d d2依次成等比数列,则
该双曲线的离心率e的取值范围是___ _.
三、解答题:(本大题6个小题,共75分)备题解答必须答在答题卡Ⅱ上(必须写出必要的
文字说明、演算步骤或推理过程)
16.(本小题满分13分)
已知命题p:关于x的不等式对任意x∈R恒成立;命题q:函数
上是增函数,若“p∨q留”为真命题,
“p∧q”为假命题,求实数a的取值范围.
17.(本小题满分13分)21世纪教育网
已知直三棱柱ABC –A1B1C1中,△ABC为等腰直角三角形,
∠BAC= 90°,且AB= AA1, D、E、F分别为B1A、C1C、BC的中点.
(1)求证:DE∥平面ABC;
(2)求证:且F⊥平面AEF;
18.(本小题满分13分)
已知函数f,函数f(x)图像在(O,f(0))处切线的斜率为-1;21世纪教育网
(1)求实数a的值;
(2)求函数f(x)的单调区间和极值.
19.(本小题满分12分)
直角梯EFCB中,EF//BC,EF=BE=BC=2,∠BEF90°,点A是平面BEF外一点,
AE⊥面BCFE,且AE=BE,G、M分别是BC、AG的中点.
(1)求证:CF⊥平面BMF;
(2)求三棱锥B-MFG的体积.
20.(本小题满分12分)
如图,已知离心率为的椭圆过点M(2,1),O为坐标原点,
平行于OM的直线,交椭圆C于不同的两点A、B.
(1)求椭圆C的方程;21世纪教育网
(2)记直线MB、MA与x轴的交点P、Q,
证明:△MPQ为等腰三角形
21.(本小题满分12分)
已知,函数.
(1)若函数f(x)在x=2处取得极值,求实数a的值。
(2)设函数g(x)=f(x)-2ax,若方程g(x)=0有唯一解,求实数a的值.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
