26.1.2 反比例函数的图象和性质(第1课时)教案
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质(第1课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 22:09:47 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
26.1 反比例函数
26.1.2反比例函数的图象和性质(第1课时)
一、教学目标
【知识与技能】
1.会用描点法画出反比例函数的图象;
2.结合图象分析并掌握反比例函数的性质.
【过程与方法】
经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想方法,让学生初步认识具体的反比例函数图象的特征.
【情感态度与价值观】
由图象的画法和分析,体验数学活动中的探索和创造性,感受数学美,并通过图象的直观教学激发学习兴趣.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
正确地进行描点、画出图象,理解并掌握反比例函数的图象和性质.
【教学难点】
归纳反比例函数的性质.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板、铅笔.
六、教学过程
(一)导入新课(出示课件2)
刘翔在2004年雅典奥运会110m栏比赛中以12.91s的成绩夺得金牌,被称为中国“飞人”.如果刘翔在比赛中跑完全程所用的时间为ts,平均速度为vm/s.
(1)你能写出用t表示v的函数表达式吗
学生回答:
(2)试一试,你能在坐标系中画出这个函数的图象吗?
(二)探索新知
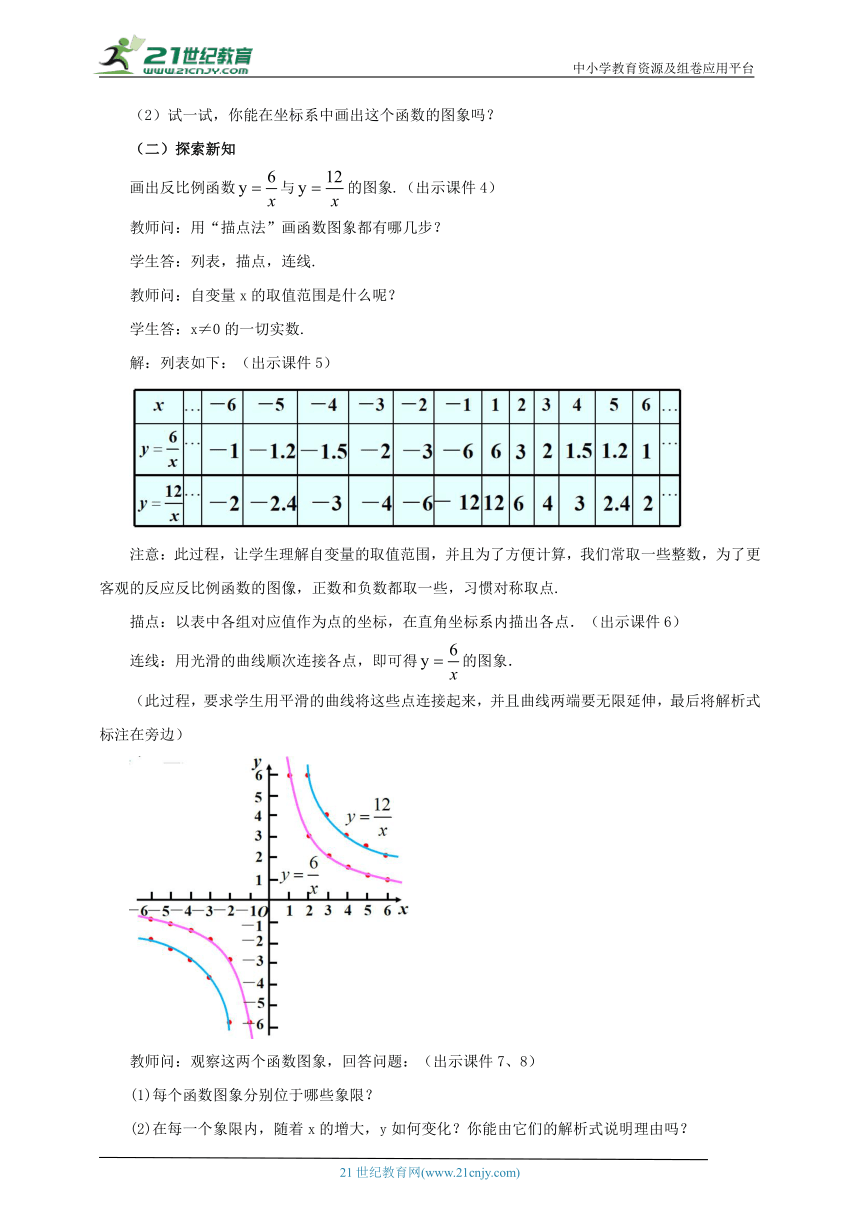
画出反比例函数与的图象.(出示课件4)
教师问:用“描点法”画函数图象都有哪几步?
学生答:列表,描点,连线.
教师问:自变量x的取值范围是什么呢?
学生答:x≠0的一切实数.
解:列表如下:(出示课件5)
注意:此过程,让学生理解自变量的取值范围,并且为了方便计算,我们常取一些整数,为了更客观的反应反比例函数的图像,正数和负数都取一些,习惯对称取点.
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出各点.(出示课件6)
连线:用光滑的曲线顺次连接各点,即可得的图象.
(此过程,要求学生用平滑的曲线将这些点连接起来,并且曲线两端要无限延伸,最后将解析式标注在旁边)
教师问:观察这两个函数图象,回答问题:(出示课件7、8)
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数(k>0),考虑问题(1)(2),你能得出同样的结论吗?
小组讨论并回答.教师订正后归纳:(出示课件9)
反比例函数(k>0)的图象和性质:
(1)由两条曲线组成,且分别位于第一、三象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而减小.
出示课件10,学生独立思考后口答,教师订正.
出示课件11:观察当k=-2,-4,-6时,反比例函数的图象,有哪些共同特征?
学生积极思考,大胆回答,理解问题.教师加以点评并纠正问题.
出示课件12:回顾上面我们利用函数图象,从特殊到一般研究反比例函数(k>0)的性质的过程,你能用类似的方法研究反比例函数(k<0)的图象和性质吗?
教师帮助学生分析问题,倾听学生的回答,订正后归纳:(出示课件13、14)
反比例函数(k<0)的图象和性质:
(1)由两条曲线组成,且分别位于第二、四象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而增大.
反比例函数的图象和性质
形状 由两支曲线组成的.因此称它的图象为双曲线
位置 当k>0时,两支双曲线分别位于第一、三象限内; 当k<0时,两支双曲线分别位于第二、四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大
图象的发展趋势 反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴
对称性 (1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数与的图象关于x轴对称,也关于y轴对称.
考点1 利用反比例函数的性质比较大小.
例 反比例函数的图象上有两点A(x1,y1),B(x2,y2),且点A,B均在该函数图象的第一象限部分,若x1>x2,则y1与y2的大小关系为( )(出示课件15)
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
师生共同分析:因为8>0,且A,B 两点均在该函数图象的第一象限部分,根据x1>x2,可知y1,y2的大小关系,即y1<y2.故选C.
出示课件16,学生独立思考后口答,教师订正.
考点2 利用反比例函数的图象和性质求字母的值.(出示课件17)
例 已知反比例函数,在每一象限内,y随x的增大而增大,求a的值.
学生独立思考后教师板演:
解:由题意得a2+a-7=-1,且a-1<0.
解得a=-3.
出示课件18,学生独立思考后解答,一生板演.
(三)课堂练习(出示课件19-25)
引导学生练习课件19-25题目,约用时20分钟。
(四)课堂小结(出示课件26)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
反比例函数的图象和性质
形状 由两支曲线组成的.因此称它的图象为双曲线
位置 当k>0时,两支双曲线分别位于第一、三象限内; 当k<0时,两支双曲线分别位于第二、四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大
图象的发展趋势 反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴
对称性 (1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数与的图象关于x轴对称,也关于y轴对称.
(五)课前预习
预习下节课(26.1.2第2课时)的相关内容.
能应用反比例函数的图象及性质解决简单的问题.
七、课后作业
教材第6页练习第1,2题.
八、板书设计
26.1.2 反比例函数的图象和性质(第1课时)
1.反比例函数的图象和性质:
2.例题
九、教学反思
本节课学生通过熟悉的描点法做出反比例函数的图像,自主通过观察,探究,合作交流,总结反比例函数的图象和性质,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.注意时间的分配.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
26.1 反比例函数
26.1.2反比例函数的图象和性质(第1课时)
一、教学目标
【知识与技能】
1.会用描点法画出反比例函数的图象;
2.结合图象分析并掌握反比例函数的性质.
【过程与方法】
经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想方法,让学生初步认识具体的反比例函数图象的特征.
【情感态度与价值观】
由图象的画法和分析,体验数学活动中的探索和创造性,感受数学美,并通过图象的直观教学激发学习兴趣.
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
正确地进行描点、画出图象,理解并掌握反比例函数的图象和性质.
【教学难点】
归纳反比例函数的性质.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板、铅笔.
六、教学过程
(一)导入新课(出示课件2)
刘翔在2004年雅典奥运会110m栏比赛中以12.91s的成绩夺得金牌,被称为中国“飞人”.如果刘翔在比赛中跑完全程所用的时间为ts,平均速度为vm/s.
(1)你能写出用t表示v的函数表达式吗
学生回答:
(2)试一试,你能在坐标系中画出这个函数的图象吗?
(二)探索新知
画出反比例函数与的图象.(出示课件4)
教师问:用“描点法”画函数图象都有哪几步?
学生答:列表,描点,连线.
教师问:自变量x的取值范围是什么呢?
学生答:x≠0的一切实数.
解:列表如下:(出示课件5)
注意:此过程,让学生理解自变量的取值范围,并且为了方便计算,我们常取一些整数,为了更客观的反应反比例函数的图像,正数和负数都取一些,习惯对称取点.
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出各点.(出示课件6)
连线:用光滑的曲线顺次连接各点,即可得的图象.
(此过程,要求学生用平滑的曲线将这些点连接起来,并且曲线两端要无限延伸,最后将解析式标注在旁边)
教师问:观察这两个函数图象,回答问题:(出示课件7、8)
(1)每个函数图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数(k>0),考虑问题(1)(2),你能得出同样的结论吗?
小组讨论并回答.教师订正后归纳:(出示课件9)
反比例函数(k>0)的图象和性质:
(1)由两条曲线组成,且分别位于第一、三象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而减小.
出示课件10,学生独立思考后口答,教师订正.
出示课件11:观察当k=-2,-4,-6时,反比例函数的图象,有哪些共同特征?
学生积极思考,大胆回答,理解问题.教师加以点评并纠正问题.
出示课件12:回顾上面我们利用函数图象,从特殊到一般研究反比例函数(k>0)的性质的过程,你能用类似的方法研究反比例函数(k<0)的图象和性质吗?
教师帮助学生分析问题,倾听学生的回答,订正后归纳:(出示课件13、14)
反比例函数(k<0)的图象和性质:
(1)由两条曲线组成,且分别位于第二、四象限,它们与x轴、y轴都不相交;
(2)在每个象限内,y随x的增大而增大.
反比例函数的图象和性质
形状 由两支曲线组成的.因此称它的图象为双曲线
位置 当k>0时,两支双曲线分别位于第一、三象限内; 当k<0时,两支双曲线分别位于第二、四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大
图象的发展趋势 反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴
对称性 (1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数与的图象关于x轴对称,也关于y轴对称.
考点1 利用反比例函数的性质比较大小.
例 反比例函数的图象上有两点A(x1,y1),B(x2,y2),且点A,B均在该函数图象的第一象限部分,若x1>x2,则y1与y2的大小关系为( )(出示课件15)
A.y1>y2 B.y1=y2 C.y1<y2 D.无法确定
师生共同分析:因为8>0,且A,B 两点均在该函数图象的第一象限部分,根据x1>x2,可知y1,y2的大小关系,即y1<y2.故选C.
出示课件16,学生独立思考后口答,教师订正.
考点2 利用反比例函数的图象和性质求字母的值.(出示课件17)
例 已知反比例函数,在每一象限内,y随x的增大而增大,求a的值.
学生独立思考后教师板演:
解:由题意得a2+a-7=-1,且a-1<0.
解得a=-3.
出示课件18,学生独立思考后解答,一生板演.
(三)课堂练习(出示课件19-25)
引导学生练习课件19-25题目,约用时20分钟。
(四)课堂小结(出示课件26)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
反比例函数的图象和性质
形状 由两支曲线组成的.因此称它的图象为双曲线
位置 当k>0时,两支双曲线分别位于第一、三象限内; 当k<0时,两支双曲线分别位于第二、四象限内
增减性 当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大
图象的发展趋势 反比例函数的图象无限接近于x、y轴,但永远不能到达x、y轴
对称性 (1)反比例函数的图象是轴对称图形,也是中心对称图形.直线y=x和y=-x都是它的对称轴;(2)反比例函数与的图象关于x轴对称,也关于y轴对称.
(五)课前预习
预习下节课(26.1.2第2课时)的相关内容.
能应用反比例函数的图象及性质解决简单的问题.
七、课后作业
教材第6页练习第1,2题.
八、板书设计
26.1.2 反比例函数的图象和性质(第1课时)
1.反比例函数的图象和性质:
2.例题
九、教学反思
本节课学生通过熟悉的描点法做出反比例函数的图像,自主通过观察,探究,合作交流,总结反比例函数的图象和性质,从而更好的理解反比例函数,并且会应用函数图像解决一些问题,渗透数形结合的思想.注意时间的分配.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
