27.2.1 相似三角形的判定(第2课时)教案
文档属性
| 名称 | 27.2.1 相似三角形的判定(第2课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 22:04:15 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
27.2 相似三角形
27.2.1相似三角形的判定(第2课时)
一、教学目标
【知识与技能】
掌握“三边成比例的两个三角形相似”的判定方法;能够运用三角形相似的条件解决简单的问题.
【过程与方法】
经历两个三角形相似的探索过程,进一步发展学生的探究、交流能力.
【情感态度与价值观】
培养学生敢于实践、勇于发现、大胆探索、合作创新的精神.
二、课型
新授课
三、课时
第2课时 共4课时
四、教学重难点
【教学重点】
三边成比例的两个三角形相似.
【教学难点】
三角形相似的判定方法的证明及运用.
五、课前准备
教师:课件、刻度尺、量角器、三角板.
学生:刻度尺、量角器、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师提出问题:学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
(二)探索新知
知识点1 三边对应成比例的两三角形相似
教师问:如何判断两个三角形是否相似 (出示课件4)
学生答:1.定义法:对应角相等,对应边的比相等的两个三角形相似.
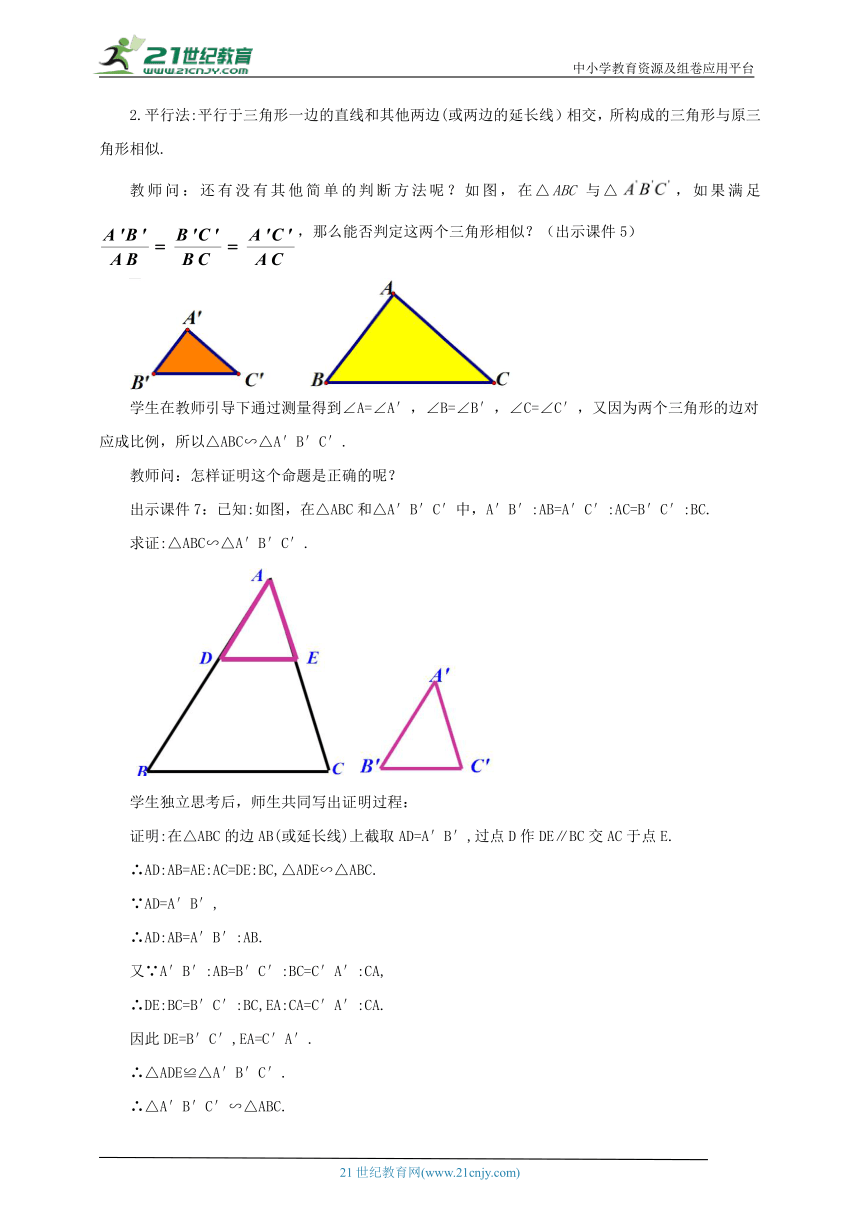
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
教师问:还有没有其他简单的判断方法呢?如图,在△ABC 与△,如果满足,那么能否判定这两个三角形相似?(出示课件5)
学生在教师引导下通过测量得到∠A=∠A′,∠B=∠B′,∠C=∠C′,又因为两个三角形的边对应成比例,所以△ABC∽△A′B′C′.
教师问:怎样证明这个命题是正确的呢?
出示课件7:已知:如图,在△ABC和△A′B′C′中,A′B′:AB=A′C′:AC=B′C′:BC.
求证:△ABC∽△A′B′C′.
学生独立思考后,师生共同写出证明过程:
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,过点D作DE∥BC交AC于点E.
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC.
∵AD=A′B′,
∴AD:AB=A′B′:AB.
又∵A′B′:AB=B′C′:BC=C′A′:CA,
∴DE:BC=B′C′:BC,EA:CA=C′A′:CA.
因此DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′.
∴△A′B′C′∽△ABC.
师生共同归纳:由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.(出示课件8)
符号语言:在△ABC 与△中,
∵
∴△ABC ∽△
教师问:在用三边的比判定两个三角形相似时,如何寻找对应边?(出示课件9)
学生讨论后教师总结:利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
考点1 利用三边成比例判断三角形相似
例 已知AB=4cm,BC=6cm,AC=8 cm,A′B′=12cm,B′C′=18 cm,A′C′=24cm,试说明△ABC∽△A′B′C′.(出示课件10)
学生独立思考后,一生板演,教师订正并强调解题书写格式.
解:∵
∴
∴△ABC∽△A′B′C′.
教师强调:判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最大边与最大边对应,最短边与最短边对应.(出示课件11)
出示课件12,学生独立思考后口答,教师订正.
考点2 判断三角形相似
例 如图,在Rt△ABC 与 Rt△A′B′C′中,∠C=∠C′=90°,且
求证:△A′B′C′∽△ABC.(出示课件13)
师生共同完成证明过程:
证明:由已知条件得AB=2A′B′,AC=2A′C′,
∴BC2=AB2-AC2=(2A′B′)2-(2A′C′)2=4A′B′2-4A′C′2
=4(A′B′2-A′C′2)=4B′C′2=(2B′C′)2.
∴ BC=2B′C′,
∴△A′B′C′∽△ABC.
出示课件14,学生独立思考后一生板演,教师订正.
考点3 利用三角形相似说明角相等
例 如图已知:试说明:∠BAD=∠CAE.(出示课件15)
学生独立思考后,师生共同解答:
解:∵
∴ΔABC∽ΔADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
出示课件16,学生独立思考后一生板演,教师订正.
(三)课堂练习(出示课件17-23)
引导学生练习课件17-23相关题目,约用时15分钟
(四)课堂小结(出示课件24)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.三两个三角形相似.
2.利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
(五)课前预习
预习下节课(27.2.1第3课时)的相关内容.
知道利用两边及夹角判定两个三角形相似的方法.
七、课后作业
教材第34页练习第1⑵,2⑴,3题.
八、板书设计
27.2.1相似三角形的判定(第2课时)
1.三边对应成比例的两个三角形相似
2.例题
九、教学反思
因为本课时教学过程中主要是让学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.在本节课中要放手给学生动脑、动手的机会,要注意面向全体学生.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2 相似三角形
27.2.1相似三角形的判定(第2课时)
一、教学目标
【知识与技能】
掌握“三边成比例的两个三角形相似”的判定方法;能够运用三角形相似的条件解决简单的问题.
【过程与方法】
经历两个三角形相似的探索过程,进一步发展学生的探究、交流能力.
【情感态度与价值观】
培养学生敢于实践、勇于发现、大胆探索、合作创新的精神.
二、课型
新授课
三、课时
第2课时 共4课时
四、教学重难点
【教学重点】
三边成比例的两个三角形相似.
【教学难点】
三角形相似的判定方法的证明及运用.
五、课前准备
教师:课件、刻度尺、量角器、三角板.
学生:刻度尺、量角器、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师提出问题:学习三角形全等时,我们知道,除了可以通过证明对应角相等.对应边相等来判定两个三角形全等外,还有判定的简便方法(SSS、SAS、ASA、AAS).类似地,判定两个三角形相似时,是不是也存在简便的判定方法呢?
类似于判定三角形全等的SSS方法,我们能不能通过三边来判断两个三角形相似呢?
(二)探索新知
知识点1 三边对应成比例的两三角形相似
教师问:如何判断两个三角形是否相似 (出示课件4)
学生答:1.定义法:对应角相等,对应边的比相等的两个三角形相似.
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
教师问:还有没有其他简单的判断方法呢?如图,在△ABC 与△,如果满足,那么能否判定这两个三角形相似?(出示课件5)
学生在教师引导下通过测量得到∠A=∠A′,∠B=∠B′,∠C=∠C′,又因为两个三角形的边对应成比例,所以△ABC∽△A′B′C′.
教师问:怎样证明这个命题是正确的呢?
出示课件7:已知:如图,在△ABC和△A′B′C′中,A′B′:AB=A′C′:AC=B′C′:BC.
求证:△ABC∽△A′B′C′.
学生独立思考后,师生共同写出证明过程:
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,过点D作DE∥BC交AC于点E.
∴AD:AB=AE:AC=DE:BC,△ADE∽△ABC.
∵AD=A′B′,
∴AD:AB=A′B′:AB.
又∵A′B′:AB=B′C′:BC=C′A′:CA,
∴DE:BC=B′C′:BC,EA:CA=C′A′:CA.
因此DE=B′C′,EA=C′A′.
∴△ADE≌△A′B′C′.
∴△A′B′C′∽△ABC.
师生共同归纳:由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.(出示课件8)
符号语言:在△ABC 与△中,
∵
∴△ABC ∽△
教师问:在用三边的比判定两个三角形相似时,如何寻找对应边?(出示课件9)
学生讨论后教师总结:利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
考点1 利用三边成比例判断三角形相似
例 已知AB=4cm,BC=6cm,AC=8 cm,A′B′=12cm,B′C′=18 cm,A′C′=24cm,试说明△ABC∽△A′B′C′.(出示课件10)
学生独立思考后,一生板演,教师订正并强调解题书写格式.
解:∵
∴
∴△ABC∽△A′B′C′.
教师强调:判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最大边与最大边对应,最短边与最短边对应.(出示课件11)
出示课件12,学生独立思考后口答,教师订正.
考点2 判断三角形相似
例 如图,在Rt△ABC 与 Rt△A′B′C′中,∠C=∠C′=90°,且
求证:△A′B′C′∽△ABC.(出示课件13)
师生共同完成证明过程:
证明:由已知条件得AB=2A′B′,AC=2A′C′,
∴BC2=AB2-AC2=(2A′B′)2-(2A′C′)2=4A′B′2-4A′C′2
=4(A′B′2-A′C′2)=4B′C′2=(2B′C′)2.
∴ BC=2B′C′,
∴△A′B′C′∽△ABC.
出示课件14,学生独立思考后一生板演,教师订正.
考点3 利用三角形相似说明角相等
例 如图已知:试说明:∠BAD=∠CAE.(出示课件15)
学生独立思考后,师生共同解答:
解:∵
∴ΔABC∽ΔADE.
∴∠BAC=∠DAE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
出示课件16,学生独立思考后一生板演,教师订正.
(三)课堂练习(出示课件17-23)
引导学生练习课件17-23相关题目,约用时15分钟
(四)课堂小结(出示课件24)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.三两个三角形相似.
2.利用三边的比判定两个三角形相似时,应先将两个三角形的三边按大小顺序排列,然后分别计算它们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
(五)课前预习
预习下节课(27.2.1第3课时)的相关内容.
知道利用两边及夹角判定两个三角形相似的方法.
七、课后作业
教材第34页练习第1⑵,2⑴,3题.
八、板书设计
27.2.1相似三角形的判定(第2课时)
1.三边对应成比例的两个三角形相似
2.例题
九、教学反思
因为本课时教学过程中主要是让学生采用类比的方法先猜想出命题,然后证明猜想的命题是否正确.课堂上教师主要还是以提问的形式,逐步引导学生去证明命题.在本节课中要放手给学生动脑、动手的机会,要注意面向全体学生.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
