27.2.1 相似三角形的判定(第1课时)教案
文档属性
| 名称 | 27.2.1 相似三角形的判定(第1课时)教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 22:03:03 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2 相似三角形
27.2.1相似三角形的判定(第1课时)
一、教学目标
【知识与技能】
1.理解相似三角形的概念,并会用以证明和计算;
2.体会用相似符号“∽”表示的相似三角形之间的边,角对应关系;
3.掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
【过程与方法】
经历平行线分线段成比例的基本事实及其推论的发现过程,增强学生发现问题,解决问题的能力.
【情感态度与价值观】
学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣.
二、课型
新授课
三、课时
第1课时 共4课时
四、教学重难点
【教学重点】
平行线分线段成比例基本事实及判定两个三角形相似的定理.
【教学难点】
判定三角形相似的定理的证明.
五、课前准备
教师:课件、刻度尺、三角板.
学生:刻度尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师问:1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A=∠A1,
∠B=∠B1,∠C=∠C1,,那么△ABC与△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
学生集体口答,教师订正.
(二)探索新知
知识点1 平行线分线段成比例定理
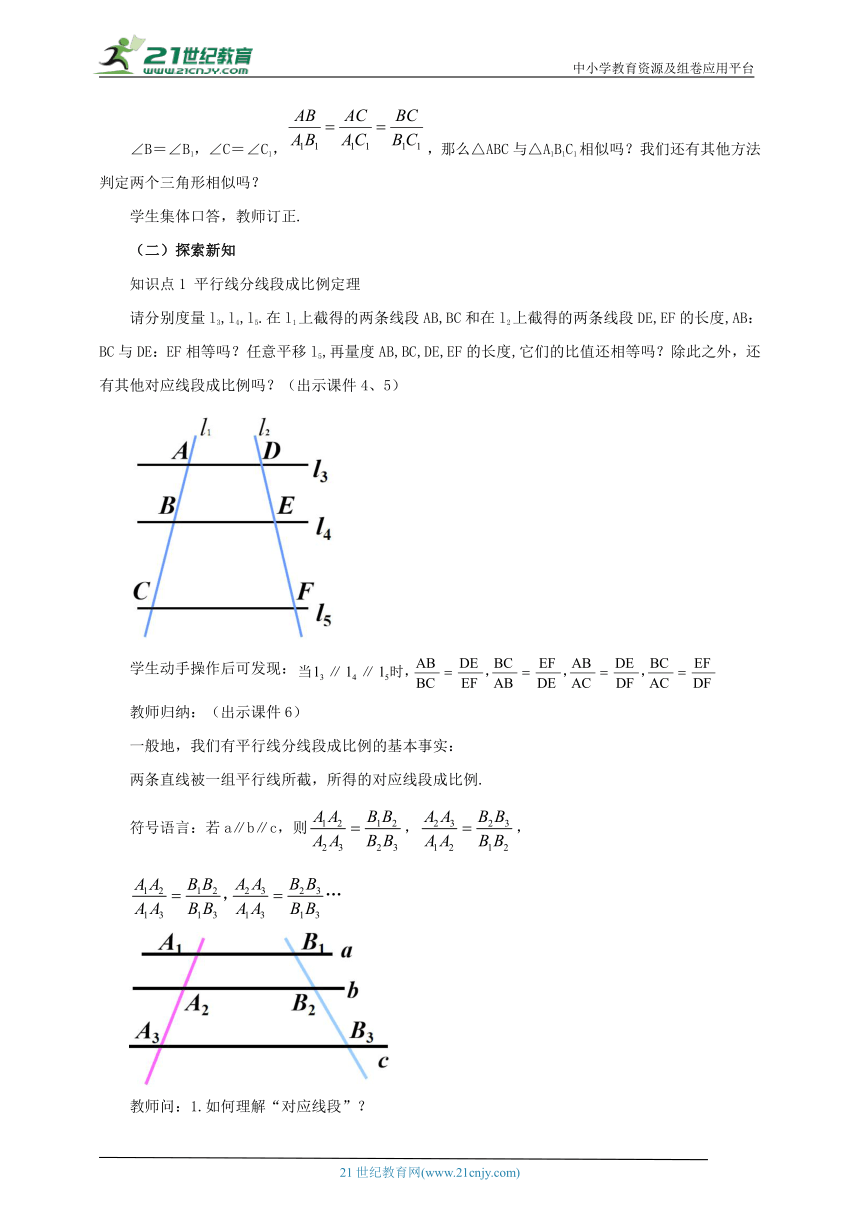
请分别度量l3,l4,l5.在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,AB:BC与DE:EF相等吗?任意平移l5,再量度AB,BC,DE,EF的长度,它们的比值还相等吗?除此之外,还有其他对应线段成比例吗?(出示课件4、5)
学生动手操作后可发现:
教师归纳:(出示课件6)
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:若a∥b∥c,则,,
教师问:1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?(出示课件7)
小组合作交流,再进行全班性的问答.
出示课件8,学生独立思考后口答,教师订正.
知识点2 平行线分线段成比例定理的推论
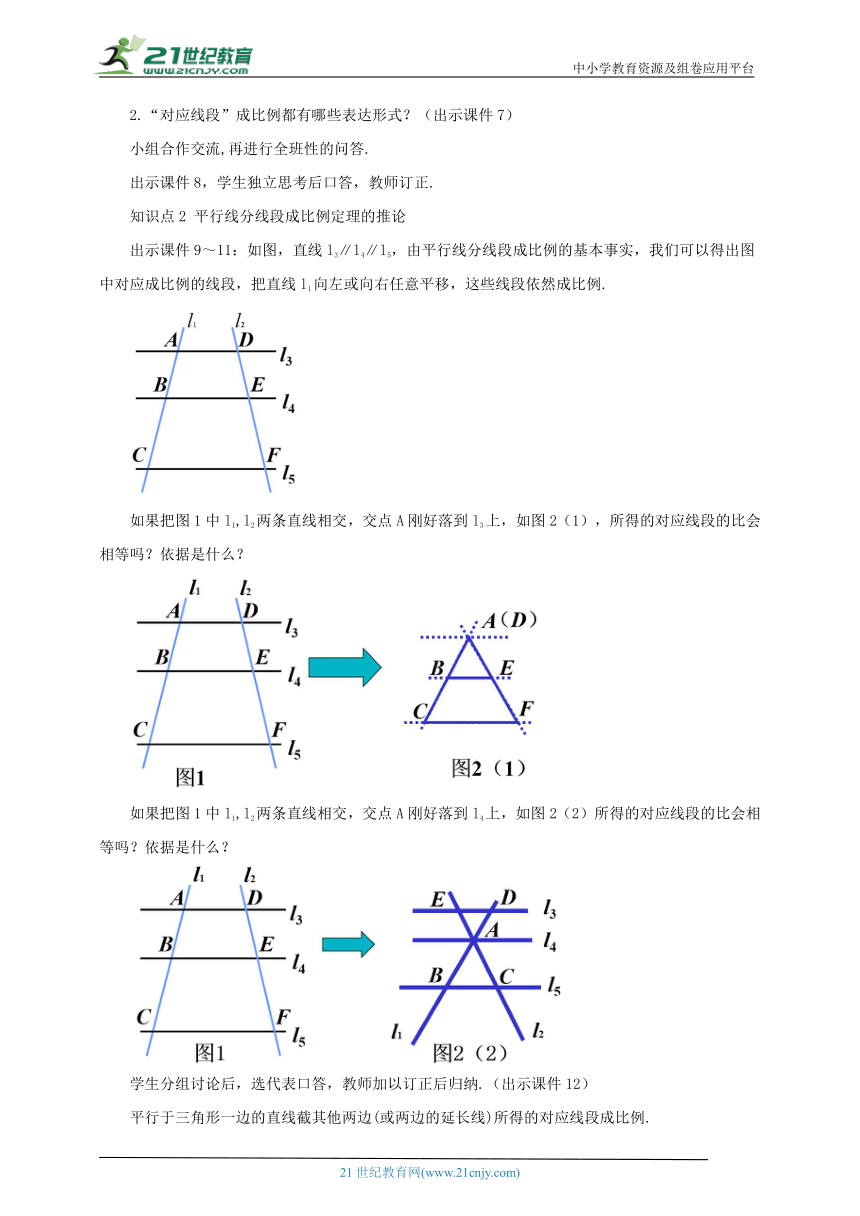
出示课件9~11:如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,把直线l1向左或向右任意平移,这些线段依然成比例.
如果把图1中l1,l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
如果把图1中l1,l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
学生分组讨论后,选代表口答,教师加以订正后归纳.(出示课件12)
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
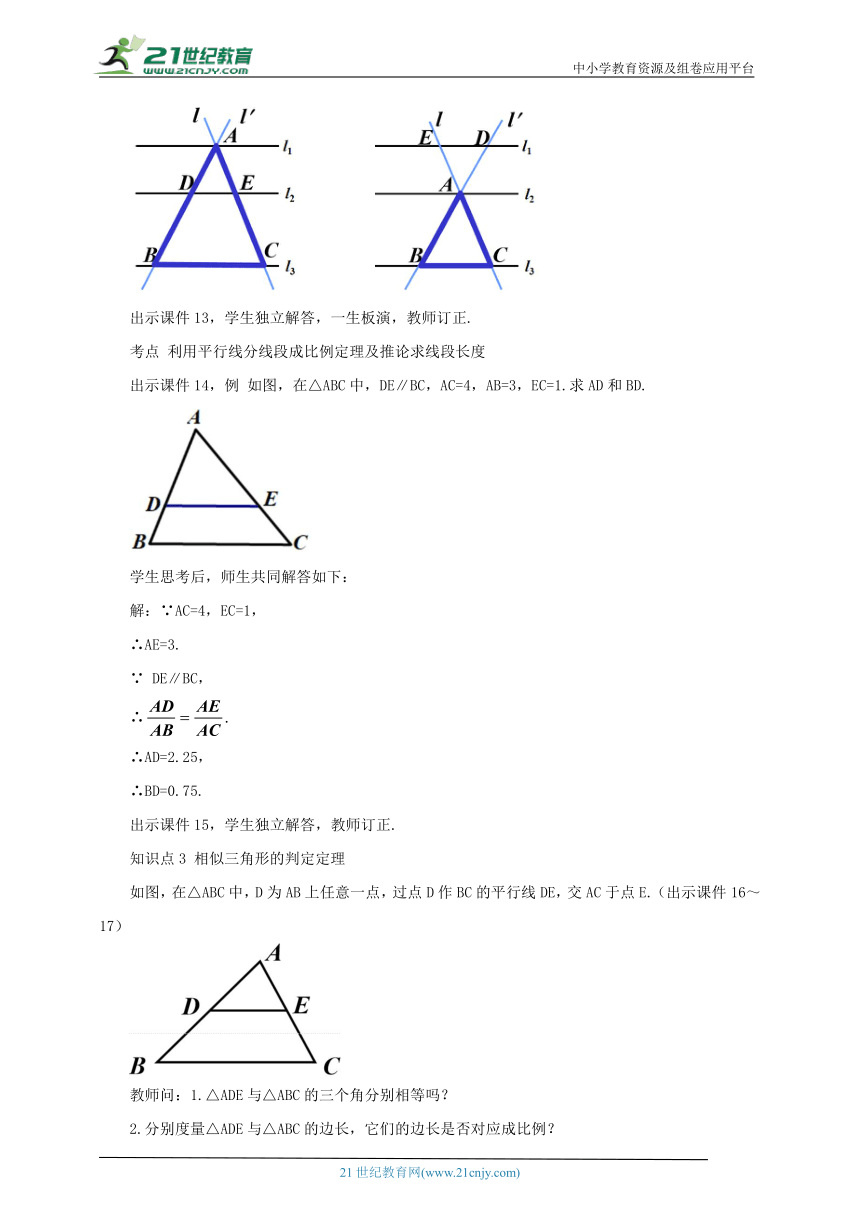
出示课件13,学生独立解答,一生板演,教师订正.
考点 利用平行线分线段成比例定理及推论求线段长度
出示课件14,例 如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1.求AD和BD.
学生思考后,师生共同解答如下:
解:∵AC=4,EC=1,
∴AE=3.
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
出示课件15,学生独立解答,教师订正.
知识点3 相似三角形的判定定理
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.(出示课件16~17)
教师问:1.△ADE与△ABC的三个角分别相等吗?
2.分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
3.你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
学生分组讨论,动手操作后达成共识:通过度量,我们发现△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
教师问:1.我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?(出示课件18)
2.由前面的结论,我们可以得到什么?还需证明什么?
学生讨论后,带着疑问解决证明△ADE∽△ABC问题.(出示课件19)
已知:如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D、E.
求证:△ADE∽△ABC.
师生共同分析:直观告诉我们:△ADE∽△ABC,根据三角形相似的概念,要想证明两个三角形相似,必须证明三个角对应相等,三条边对应边对应成比例.由平行线分线段成比例定理,可知:,还需证明所以要将DE平移到BC上,使得BF=DE(如图),再证明:即可.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C,
过E作EF//AB交BC于F,则,
∵四边形DBFE是平行四边形,
∴DE=BF,
∴,
∴,
∴△ADE∽△ABC.
归纳:定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.(出示课件20)
符号语言:∵DE//BC,∴△ADE∽△ABC.
教师问:过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?(出示课件21)
学生分组讨论后,教师归纳:过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
出示课件22,学生独立思考后口答,教师订正.
(三)课堂练习(出示课件23-29)
引导学生练习课件23-29题目,巩固本课知识点,约用时20分钟。
(四)课堂小结(出示课件30)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.两条直线被一组平行线所截,所得的对应线段成比例.
2.平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
3.平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
(五)课前预习
预习下节课(27.2.1第2课时)的相关内容.
知道利用三边判定两个三角形相似的方法.
七、课后作业
教材第31页练习第1,2题.
八、板书设计
27.2.1相似三角形的判定(第1课时)
1.定义 5.例题
2.基本事实
3.推论
4.判定定理
九、教学反思
关于平行线分线段成比例定理,学生没有足够体验,很难达到对定理的理解,进而影响了后续知识的掌握.所有的新知识,都要通过自身“再创造”,纳入到自己的认知结构中,成为有效而能发展的知识,优化和发展了数学认知结构.因此在教学过程中,要让学生经历“观察——猜想——归纳——验证”等一系列的数学活动,不断体会数形结合和从特殊到一般的数学思想方法.要给学生充足的研讨时间,化未知为已知,从而不断完善学生的认知体系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2 相似三角形
27.2.1相似三角形的判定(第1课时)
一、教学目标
【知识与技能】
1.理解相似三角形的概念,并会用以证明和计算;
2.体会用相似符号“∽”表示的相似三角形之间的边,角对应关系;
3.掌握平行线分线段成比例的基本事实及其推论的应用,会用平行线判定两个三角形相似并进行证明和计算.
【过程与方法】
经历平行线分线段成比例的基本事实及其推论的发现过程,增强学生发现问题,解决问题的能力.
【情感态度与价值观】
学生在充分经历自学、探究、交流、当堂练习等活动中,获得成功的体验,调动主动学习的积极性,感受数学学习的乐趣.
二、课型
新授课
三、课时
第1课时 共4课时
四、教学重难点
【教学重点】
平行线分线段成比例基本事实及判定两个三角形相似的定理.
【教学难点】
判定三角形相似的定理的证明.
五、课前准备
教师:课件、刻度尺、三角板.
学生:刻度尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师问:1.相似多边形的特征是什么?
2.怎样判定两个多边形相似?
3.什么叫相似比?
4.相似多边形中,最简单的就是相似三角形.如果∠A=∠A1,
∠B=∠B1,∠C=∠C1,,那么△ABC与△A1B1C1相似吗?我们还有其他方法判定两个三角形相似吗?
学生集体口答,教师订正.
(二)探索新知
知识点1 平行线分线段成比例定理
请分别度量l3,l4,l5.在l1上截得的两条线段AB,BC和在l2上截得的两条线段DE,EF的长度,AB:BC与DE:EF相等吗?任意平移l5,再量度AB,BC,DE,EF的长度,它们的比值还相等吗?除此之外,还有其他对应线段成比例吗?(出示课件4、5)
学生动手操作后可发现:
教师归纳:(出示课件6)
一般地,我们有平行线分线段成比例的基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
符号语言:若a∥b∥c,则,,
教师问:1.如何理解“对应线段”?
2.“对应线段”成比例都有哪些表达形式?(出示课件7)
小组合作交流,再进行全班性的问答.
出示课件8,学生独立思考后口答,教师订正.
知识点2 平行线分线段成比例定理的推论
出示课件9~11:如图,直线l3∥l4∥l5,由平行线分线段成比例的基本事实,我们可以得出图中对应成比例的线段,把直线l1向左或向右任意平移,这些线段依然成比例.
如果把图1中l1,l2两条直线相交,交点A刚好落到l3上,如图2(1),所得的对应线段的比会相等吗?依据是什么?
如果把图1中l1,l2两条直线相交,交点A刚好落到l4上,如图2(2)所得的对应线段的比会相等吗?依据是什么?
学生分组讨论后,选代表口答,教师加以订正后归纳.(出示课件12)
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
出示课件13,学生独立解答,一生板演,教师订正.
考点 利用平行线分线段成比例定理及推论求线段长度
出示课件14,例 如图,在△ABC中,DE∥BC,AC=4,AB=3,EC=1.求AD和BD.
学生思考后,师生共同解答如下:
解:∵AC=4,EC=1,
∴AE=3.
∵ DE∥BC,
∴
∴AD=2.25,
∴BD=0.75.
出示课件15,学生独立解答,教师订正.
知识点3 相似三角形的判定定理
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.(出示课件16~17)
教师问:1.△ADE与△ABC的三个角分别相等吗?
2.分别度量△ADE与△ABC的边长,它们的边长是否对应成比例?
3.你认为△ADE与△ABC之间有什么关系?平行移动DE的位置,你的结论还成立吗?
学生分组讨论,动手操作后达成共识:通过度量,我们发现△ADE∽△ABC,且只要DE∥BC,这个结论恒成立.
教师问:1.我们通过度量三角形的边长,知道△ADE∽△ABC,但要用相似的定义去证明它,我们需要证明什么?(出示课件18)
2.由前面的结论,我们可以得到什么?还需证明什么?
学生讨论后,带着疑问解决证明△ADE∽△ABC问题.(出示课件19)
已知:如图,在△ABC中,DE//BC,且DE分别交AB,AC于点D、E.
求证:△ADE∽△ABC.
师生共同分析:直观告诉我们:△ADE∽△ABC,根据三角形相似的概念,要想证明两个三角形相似,必须证明三个角对应相等,三条边对应边对应成比例.由平行线分线段成比例定理,可知:,还需证明所以要将DE平移到BC上,使得BF=DE(如图),再证明:即可.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C,
过E作EF//AB交BC于F,则,
∵四边形DBFE是平行四边形,
∴DE=BF,
∴,
∴,
∴△ADE∽△ABC.
归纳:定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似.(出示课件20)
符号语言:∵DE//BC,∴△ADE∽△ABC.
教师问:过点D作与AC平行的直线与BC相交,可否证明△ADE∽△ABC?如果在三角形中出现一边的平行线,那么你应该联想到什么?(出示课件21)
学生分组讨论后,教师归纳:过点D作与AC平行的直线与BC相交,仍可证明△ADE∽△ABC,这与教材第31页证法雷同.题目中有平行线,可得相似三角形,然后利用相似三角形的性质,可列出比例式.
出示课件22,学生独立思考后口答,教师订正.
(三)课堂练习(出示课件23-29)
引导学生练习课件23-29题目,巩固本课知识点,约用时20分钟。
(四)课堂小结(出示课件30)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.两条直线被一组平行线所截,所得的对应线段成比例.
2.平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
3.平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.
(五)课前预习
预习下节课(27.2.1第2课时)的相关内容.
知道利用三边判定两个三角形相似的方法.
七、课后作业
教材第31页练习第1,2题.
八、板书设计
27.2.1相似三角形的判定(第1课时)
1.定义 5.例题
2.基本事实
3.推论
4.判定定理
九、教学反思
关于平行线分线段成比例定理,学生没有足够体验,很难达到对定理的理解,进而影响了后续知识的掌握.所有的新知识,都要通过自身“再创造”,纳入到自己的认知结构中,成为有效而能发展的知识,优化和发展了数学认知结构.因此在教学过程中,要让学生经历“观察——猜想——归纳——验证”等一系列的数学活动,不断体会数形结合和从特殊到一般的数学思想方法.要给学生充足的研讨时间,化未知为已知,从而不断完善学生的认知体系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
