27.2.2 相似三角形的性质 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2 相似三角形
27.2.2相似三角形的性质
一、教学目标
【知识与技能】
1.相似三角形的一切对应线段的比都等于相似比;
2.理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方;
3.能用三角形的性质解决简单的问题.
【过程与方法】
通过操作、观察、猜想、类比等活动,进一步提高学生的思维能力和推理论证能力.
【情感态度与价值观】
通过对性质的发现和论证,可以提高学生学习数学的热情,增强学生的探究意识,引发学生学习数学的兴趣.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
相似三角形性质定理的理解与运用.
【教学难点】
探究相似三角形面积的性质,并运用相似三角形的性质定理解决问题.
五、课前准备
教师:课件、直尺、三角板.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2、3)
教师问:相似三角形的判定方法有哪几种?
学生答:1.对应边成比例,对应角相等的两个三角形相似.
2.平行于三角形一边,与另外两边相交所构成的三角形与原三角形相似.
3.三边对应成比例的两三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
5.两角分别相等的两个三角形相似.
6.两边对应成比例的两直角三角形相似.
教师问:三角形除了三个角,三条边外,还有哪些几何量
学生答:角平分线、高线、中线、周长、面积.
教师问:如果两个三角形相似,那么它们的这些几何量有一些怎样的性质呢
(二)探索新知
知识点1 相似三角形对应线段的比
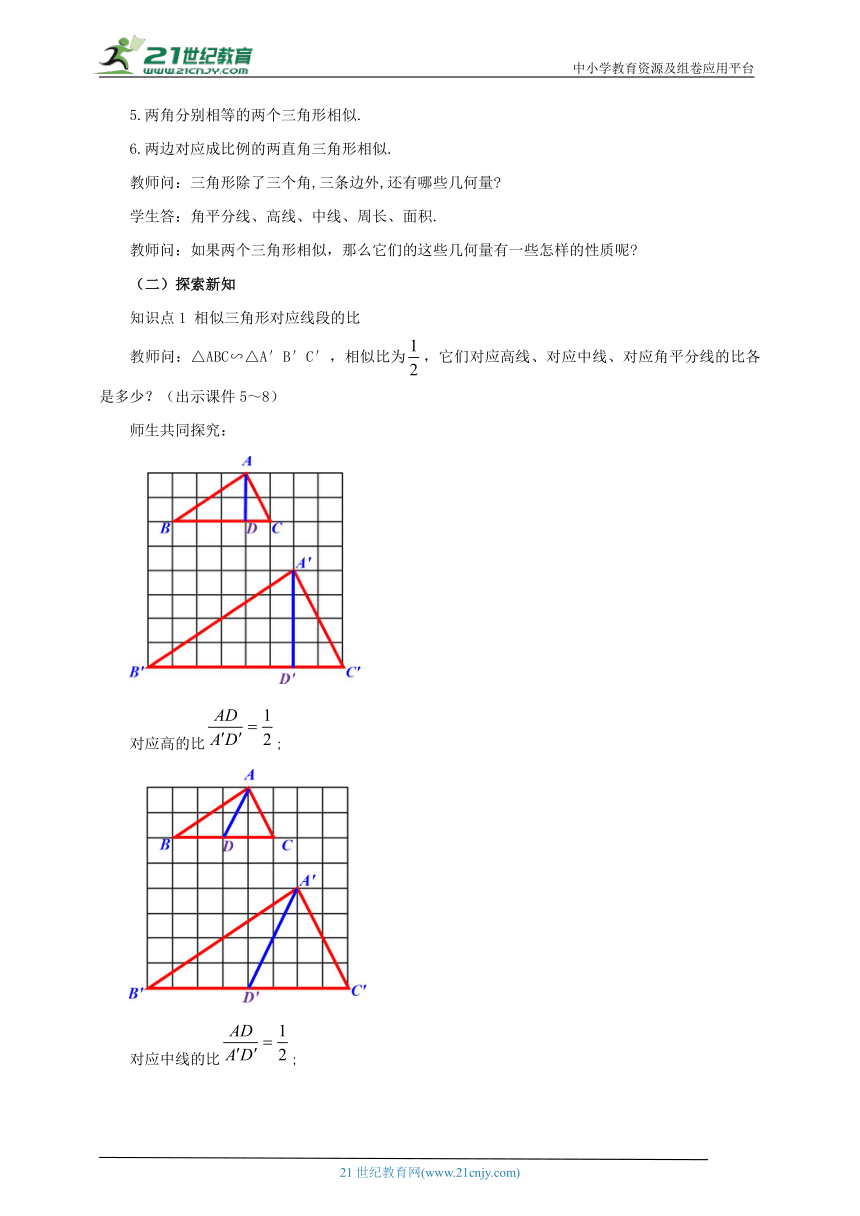
教师问:△ABC∽△A′B′C′,相似比为,它们对应高线、对应中线、对应角平分线的比各是多少?(出示课件5~8)
师生共同探究:
对应高的比;
对应中线的比;
对应角平分线的比.
教师问:△ABC∽△A′B′C′,若相似比为k,它们对应高、对应中线、对应角平分线的比又各是多少?(出示课件9)
师生共同探究:
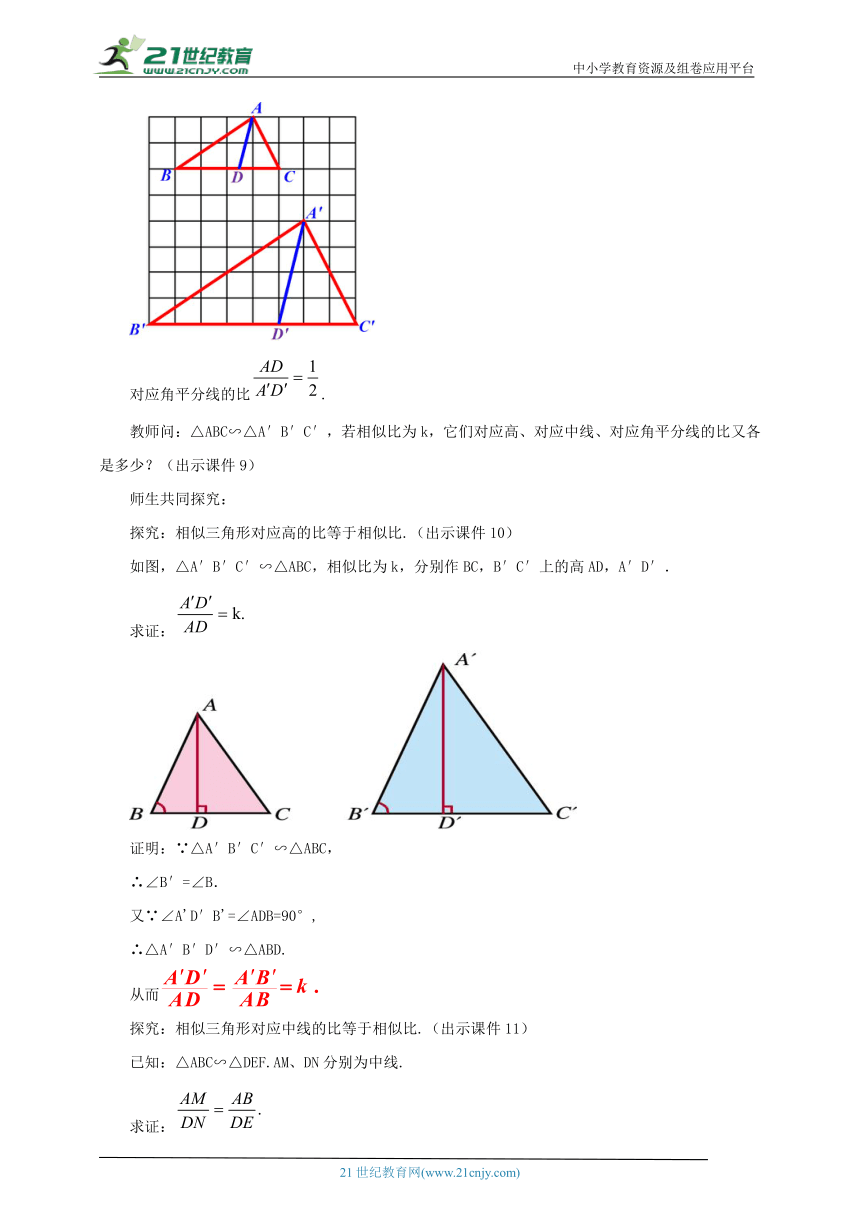
探究:相似三角形对应高的比等于相似比.(出示课件10)
如图,△A′B′C′∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
证明:∵△A′B′C′∽△ABC,
∴∠B′=∠B.
又∵∠A'D′B'=∠ADB=90°,
∴△A′B′D′∽△ABD.
从而
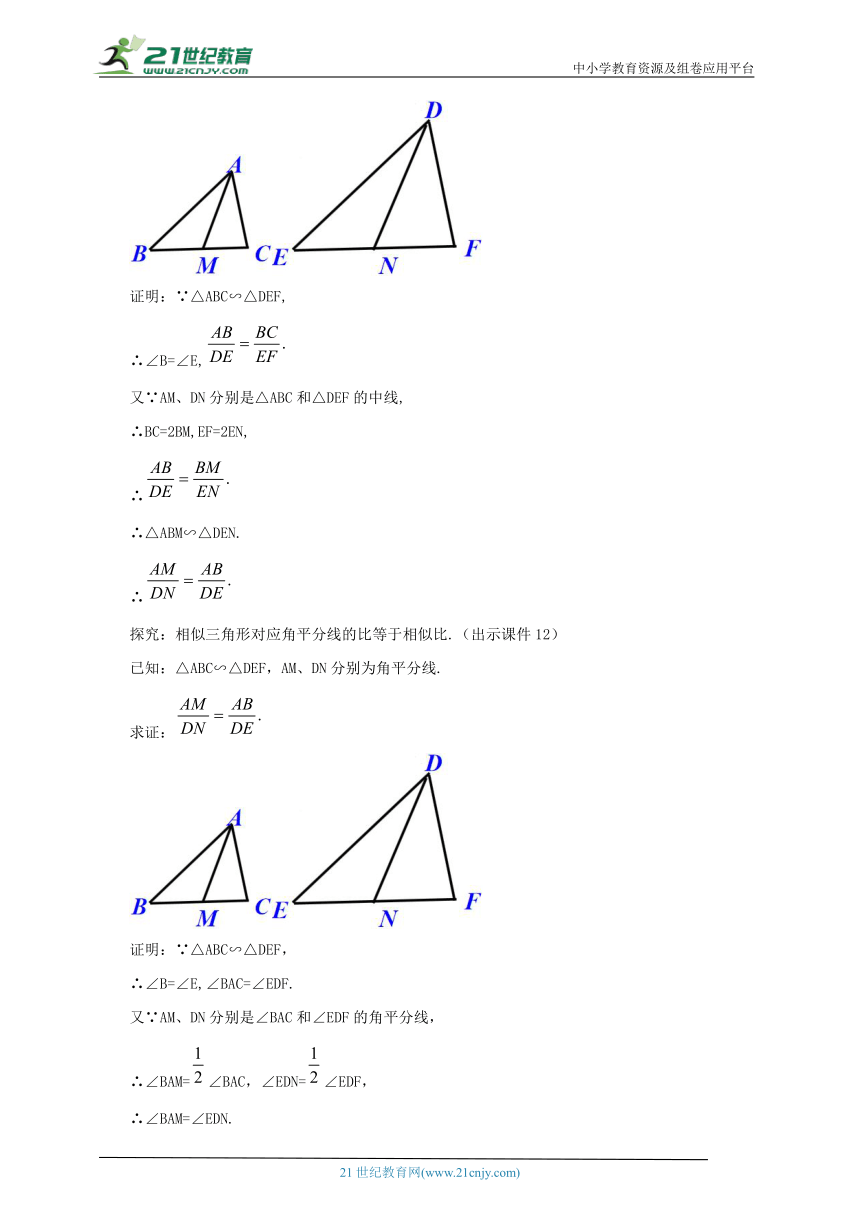
探究:相似三角形对应中线的比等于相似比.(出示课件11)
已知:△ABC∽△DEF.AM、DN分别为中线.
求证:
证明:∵△ABC∽△DEF,
∴∠B=∠E,
又∵AM、DN分别是△ABC和△DEF的中线,
∴BC=2BM,EF=2EN,
∴
∴△ABM∽△DEN.
∴
探究:相似三角形对应角平分线的比等于相似比.(出示课件12)
已知:△ABC∽△DEF,AM、DN分别为角平分线.
求证:
证明:∵△ABC∽△DEF,
∴∠B=∠E,∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠BAC,∠EDN=∠EDF,
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴
归纳总结:相似三角形对应高的比等于相似比.(出示课件13)
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
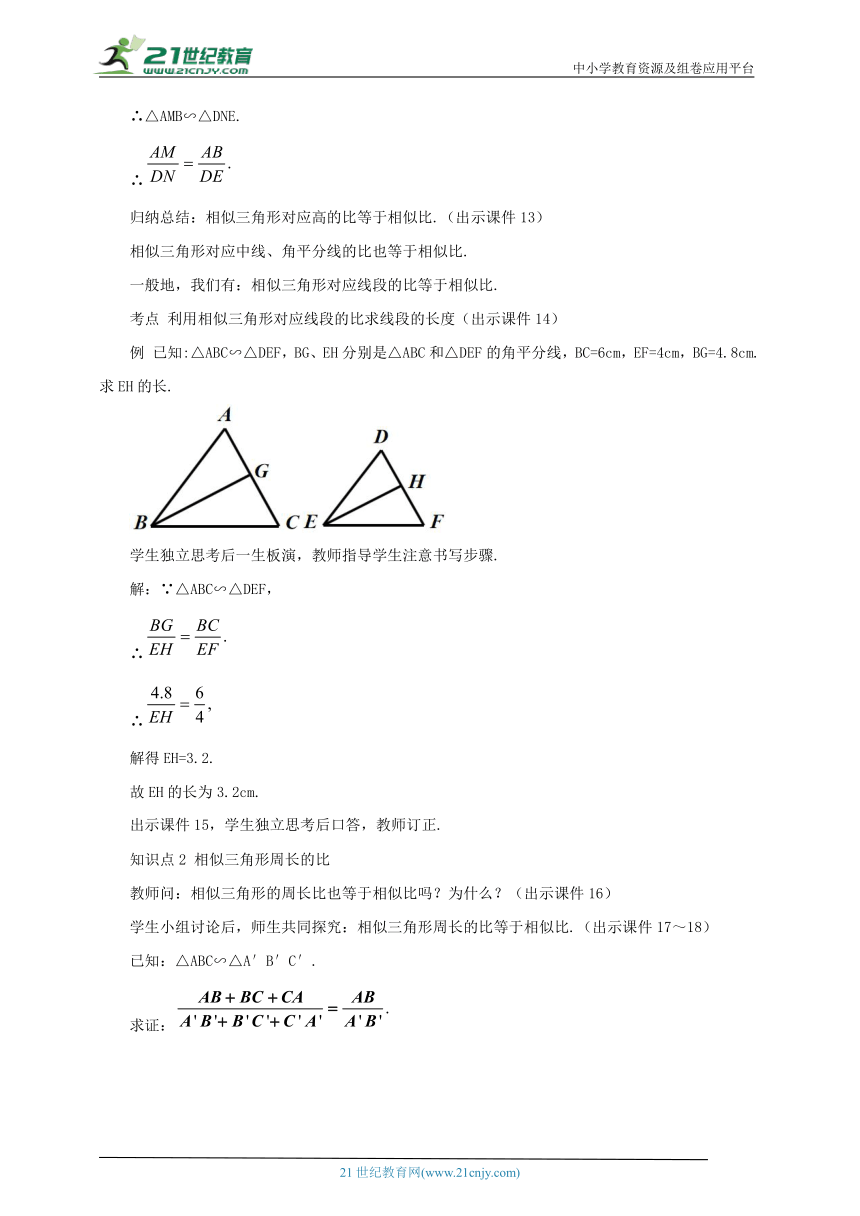
考点 利用相似三角形对应线段的比求线段的长度(出示课件14)
例 已知:△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
学生独立思考后一生板演,教师指导学生注意书写步骤.
解:∵△ABC∽△DEF,
∴
∴
解得EH=3.2.
故EH的长为3.2cm.
出示课件15,学生独立思考后口答,教师订正.
知识点2 相似三角形周长的比
教师问:相似三角形的周长比也等于相似比吗?为什么?(出示课件16)
学生小组讨论后,师生共同探究:相似三角形周长的比等于相似比.(出示课件17~18)
已知:△ABC∽△A′B′C′.
求证:
证明1:∵△ABC∽△A′B′C′,
∴
∴
证明2:∵△ABC∽△A′B′C′,相似比为k,
∴
∴AB=kA′B′,BC=kB′C′,AC=kA′C′,
.
出示课件19,学生独立思考后口答,教师订正.
知识点3 相似三角形面积的比
教师问:△ABC∽△A′B′C′,相似比为k,它们的面积比是多少?(出示课件20)
学生讨论后,师生共同探究如下:(出示课件21)
由前面的结论,我们有
==·=k· k= k2
教师归纳:(出示课件22)
相似三角形性质定理:相似三角形面积的比等于相似比的平方.
几何表述:∵△ABC∽△A′B′C′,相似比为k,
∴.
出示课件23,学生独立思考后填表,教师订正.
考点1 利用相似三角形面积的比求面积或线段
例 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为,求△DEF的边EF上的高和面积.(出示课件24~25)
学生独立思考后,师生共同解答:
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴
又∵∠D=∠A,
∴△DEF∽△ABC,相似比为1:2.
∵△ABC的边BC上的高为6,面积为,
∴△DEF的边EF上的高为,
面积为
出示课件26,学生独立思考后口答,教师订正.
考点2 利用相似三角形面积的比求多边形的面积(比)
例 如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且,求四边形BCDE的面积.(出示课件27)
学生小组讨论后,一生板演,教师指正.
解:∵∠BAC=∠DAE,且,
∴△ADE∽△ABC.
∵它们的相似比为3:5,
∴面积比为9:25.
又∵△ABC的面积为100cm2,
∴△ADE的面积为36cm2.
∴四边形BCDE的面积为100-36=64(cm2).
出示课件28~29,学生自主解决,一生板演,教师巡视指导,然后多媒体展示验证.
(三)课堂练习(出示课件30-37)
引导学生练习课件30-37题目,约用时20分钟。
(四)课堂小结(出示课件38)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.相似三角形对应中线、角平分线、对应高的比等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
2.相似三角形的周长比等于相似比.
3.相似三角形面积的比等于相似比的平方.
(五)课前预习
预习下节课(27.2.3)的相关内容.
能利用相似三角形解决一些简单问题.
七、课后作业
教材第39页练习第1,3题.
八、板书设计
27.2.2相似三角形的性质
1.相似三角形的对应线段的比也等于相似比 4.例题
2.相似三角形的周长的比等于相似比
3.相似三角形的面积的比等于相似比的平方
九、教学反思
本节课让学生在学习探究中,体会、理解、掌握相似三角形的对应中线、对应高、对应角平分线及周长比等于相似比,面积比等于相似比的平方.并通过类比的方法得出上述结论.此外,教师的肯定、表扬与鼓励,会使学生始终保持高昂的学习热情,感受在探究性学习、创造性劳动中获得成功的乐趣这样的时常诱导学生积极探索、思考,既能达到掌握知识,又能提高能力,才能使学生学会学习.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2 相似三角形
27.2.2相似三角形的性质
一、教学目标
【知识与技能】
1.相似三角形的一切对应线段的比都等于相似比;
2.理解并初步掌握相似三角形周长的比等于相似比,面积的比等于相似比的平方;
3.能用三角形的性质解决简单的问题.
【过程与方法】
通过操作、观察、猜想、类比等活动,进一步提高学生的思维能力和推理论证能力.
【情感态度与价值观】
通过对性质的发现和论证,可以提高学生学习数学的热情,增强学生的探究意识,引发学生学习数学的兴趣.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
相似三角形性质定理的理解与运用.
【教学难点】
探究相似三角形面积的性质,并运用相似三角形的性质定理解决问题.
五、课前准备
教师:课件、直尺、三角板.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2、3)
教师问:相似三角形的判定方法有哪几种?
学生答:1.对应边成比例,对应角相等的两个三角形相似.
2.平行于三角形一边,与另外两边相交所构成的三角形与原三角形相似.
3.三边对应成比例的两三角形相似.
4.两边成比例且夹角相等的两个三角形相似.
5.两角分别相等的两个三角形相似.
6.两边对应成比例的两直角三角形相似.
教师问:三角形除了三个角,三条边外,还有哪些几何量
学生答:角平分线、高线、中线、周长、面积.
教师问:如果两个三角形相似,那么它们的这些几何量有一些怎样的性质呢
(二)探索新知
知识点1 相似三角形对应线段的比
教师问:△ABC∽△A′B′C′,相似比为,它们对应高线、对应中线、对应角平分线的比各是多少?(出示课件5~8)
师生共同探究:
对应高的比;
对应中线的比;
对应角平分线的比.
教师问:△ABC∽△A′B′C′,若相似比为k,它们对应高、对应中线、对应角平分线的比又各是多少?(出示课件9)
师生共同探究:
探究:相似三角形对应高的比等于相似比.(出示课件10)
如图,△A′B′C′∽△ABC,相似比为k,分别作BC,B′C′上的高AD,A′D′.
求证:
证明:∵△A′B′C′∽△ABC,
∴∠B′=∠B.
又∵∠A'D′B'=∠ADB=90°,
∴△A′B′D′∽△ABD.
从而
探究:相似三角形对应中线的比等于相似比.(出示课件11)
已知:△ABC∽△DEF.AM、DN分别为中线.
求证:
证明:∵△ABC∽△DEF,
∴∠B=∠E,
又∵AM、DN分别是△ABC和△DEF的中线,
∴BC=2BM,EF=2EN,
∴
∴△ABM∽△DEN.
∴
探究:相似三角形对应角平分线的比等于相似比.(出示课件12)
已知:△ABC∽△DEF,AM、DN分别为角平分线.
求证:
证明:∵△ABC∽△DEF,
∴∠B=∠E,∠BAC=∠EDF.
又∵AM、DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠BAC,∠EDN=∠EDF,
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
∴
归纳总结:相似三角形对应高的比等于相似比.(出示课件13)
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
考点 利用相似三角形对应线段的比求线段的长度(出示课件14)
例 已知:△ABC∽△DEF,BG、EH分别是△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
学生独立思考后一生板演,教师指导学生注意书写步骤.
解:∵△ABC∽△DEF,
∴
∴
解得EH=3.2.
故EH的长为3.2cm.
出示课件15,学生独立思考后口答,教师订正.
知识点2 相似三角形周长的比
教师问:相似三角形的周长比也等于相似比吗?为什么?(出示课件16)
学生小组讨论后,师生共同探究:相似三角形周长的比等于相似比.(出示课件17~18)
已知:△ABC∽△A′B′C′.
求证:
证明1:∵△ABC∽△A′B′C′,
∴
∴
证明2:∵△ABC∽△A′B′C′,相似比为k,
∴
∴AB=kA′B′,BC=kB′C′,AC=kA′C′,
.
出示课件19,学生独立思考后口答,教师订正.
知识点3 相似三角形面积的比
教师问:△ABC∽△A′B′C′,相似比为k,它们的面积比是多少?(出示课件20)
学生讨论后,师生共同探究如下:(出示课件21)
由前面的结论,我们有
==·=k· k= k2
教师归纳:(出示课件22)
相似三角形性质定理:相似三角形面积的比等于相似比的平方.
几何表述:∵△ABC∽△A′B′C′,相似比为k,
∴.
出示课件23,学生独立思考后填表,教师订正.
考点1 利用相似三角形面积的比求面积或线段
例 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为,求△DEF的边EF上的高和面积.(出示课件24~25)
学生独立思考后,师生共同解答:
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴
又∵∠D=∠A,
∴△DEF∽△ABC,相似比为1:2.
∵△ABC的边BC上的高为6,面积为,
∴△DEF的边EF上的高为,
面积为
出示课件26,学生独立思考后口答,教师订正.
考点2 利用相似三角形面积的比求多边形的面积(比)
例 如图,D,E分别是AC,AB上的点,已知△ABC的面积为100cm2,且,求四边形BCDE的面积.(出示课件27)
学生小组讨论后,一生板演,教师指正.
解:∵∠BAC=∠DAE,且,
∴△ADE∽△ABC.
∵它们的相似比为3:5,
∴面积比为9:25.
又∵△ABC的面积为100cm2,
∴△ADE的面积为36cm2.
∴四边形BCDE的面积为100-36=64(cm2).
出示课件28~29,学生自主解决,一生板演,教师巡视指导,然后多媒体展示验证.
(三)课堂练习(出示课件30-37)
引导学生练习课件30-37题目,约用时20分钟。
(四)课堂小结(出示课件38)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.相似三角形对应中线、角平分线、对应高的比等于相似比.
一般地,我们有:相似三角形对应线段的比等于相似比.
2.相似三角形的周长比等于相似比.
3.相似三角形面积的比等于相似比的平方.
(五)课前预习
预习下节课(27.2.3)的相关内容.
能利用相似三角形解决一些简单问题.
七、课后作业
教材第39页练习第1,3题.
八、板书设计
27.2.2相似三角形的性质
1.相似三角形的对应线段的比也等于相似比 4.例题
2.相似三角形的周长的比等于相似比
3.相似三角形的面积的比等于相似比的平方
九、教学反思
本节课让学生在学习探究中,体会、理解、掌握相似三角形的对应中线、对应高、对应角平分线及周长比等于相似比,面积比等于相似比的平方.并通过类比的方法得出上述结论.此外,教师的肯定、表扬与鼓励,会使学生始终保持高昂的学习热情,感受在探究性学习、创造性劳动中获得成功的乐趣这样的时常诱导学生积极探索、思考,既能达到掌握知识,又能提高能力,才能使学生学会学习.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
