27.2.3 相似三角形应用举例 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2 相似三角形
27.2.3相似三角形应用举例
一、教学目标
【知识与技能】
1.应用相似三角形的有关知识去解决简单的实际问题;
2.应用三角形相似的知识计算不能直接测量物体的长度和高度.
【过程与方法】
经历应用相似三角形的有关知识去解决简单的实际问题的全过程,培养学生的应用意识和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力.
【情感态度与价值观】
1.通过著名的科学家如何测量神秘的金字塔的高度来激发学生学数学的兴趣,使全体学生积极参与探索,体验成功的喜悦;
2.力求培养学生科学,正确的数学观,体现探索精神.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
运用三角形相似的知识计算不能直接测量物体的长度和高度.
【教学难点】
通过审题、思考后,如何在实际问题中抽象出相似三角形的模型.
五、课前准备
教师:课件、直尺、三角板.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师问:在前面,我们学过哪些判定三角形相似的方法?相似三角形的性质是什么?
学生答:1.相似三角形的判定:
(1) 通过平行线;(2) 三边成比例;(3) 两边成比例且夹角相等;(4) 两角分别相等.
2.相似三角形的性质:
(1)对应边成比例,对应角相等;
(2)相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方.
教师问:观察下列图片,你会利用相似三角形知识解决一些不能直接测量的物体(如塔高、河宽等)的长度或高度的问题吗?
出示课件3~7,学生思考解决方法.
教师提示:利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.(出示课件7)
(二)探索新知
知识点1 利用相似三角形测物体
古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度.(出示课件9)
考点1 利用相似三角形测物体的高(出示课件10)
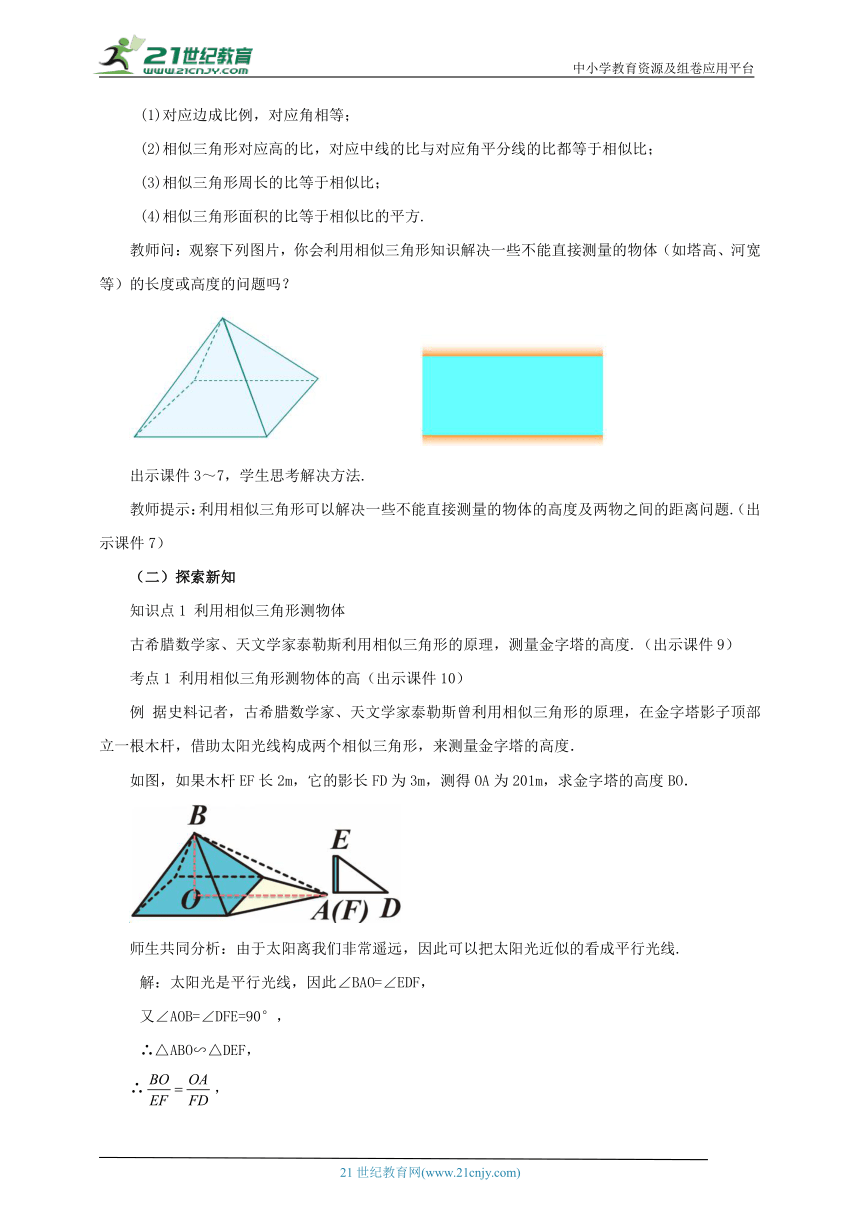
例 据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
师生共同分析:由于太阳离我们非常遥远,因此可以把太阳光近似的看成平行光线.
解:太阳光是平行光线,因此∠BAO=∠EDF,
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴,
∴(m).
因此金字塔的高度为134m.
教师问:利用太阳光测量物体的高度一般需要注意哪些问题?(出示课件11)
学生分组讨论后教师总结:在同一时刻,太阳光下不同物体的高度之比与其影长之比相等.利用太阳光测量物体的高度需要注意:
(1)由于太阳相对于地面的位置在不停地改变,影长也随着太阳位置的变化而发生变化,因此要在同一时刻测量影长.
(2)被测物体的底部必须在可以到达的地方,否则,测不到被测物体的影长,从而计算不出物体的高.
(3)表达式:物1高:物2高=影1长:影2长.
出示课件12,学生独立思考后一生板演,教师订正.
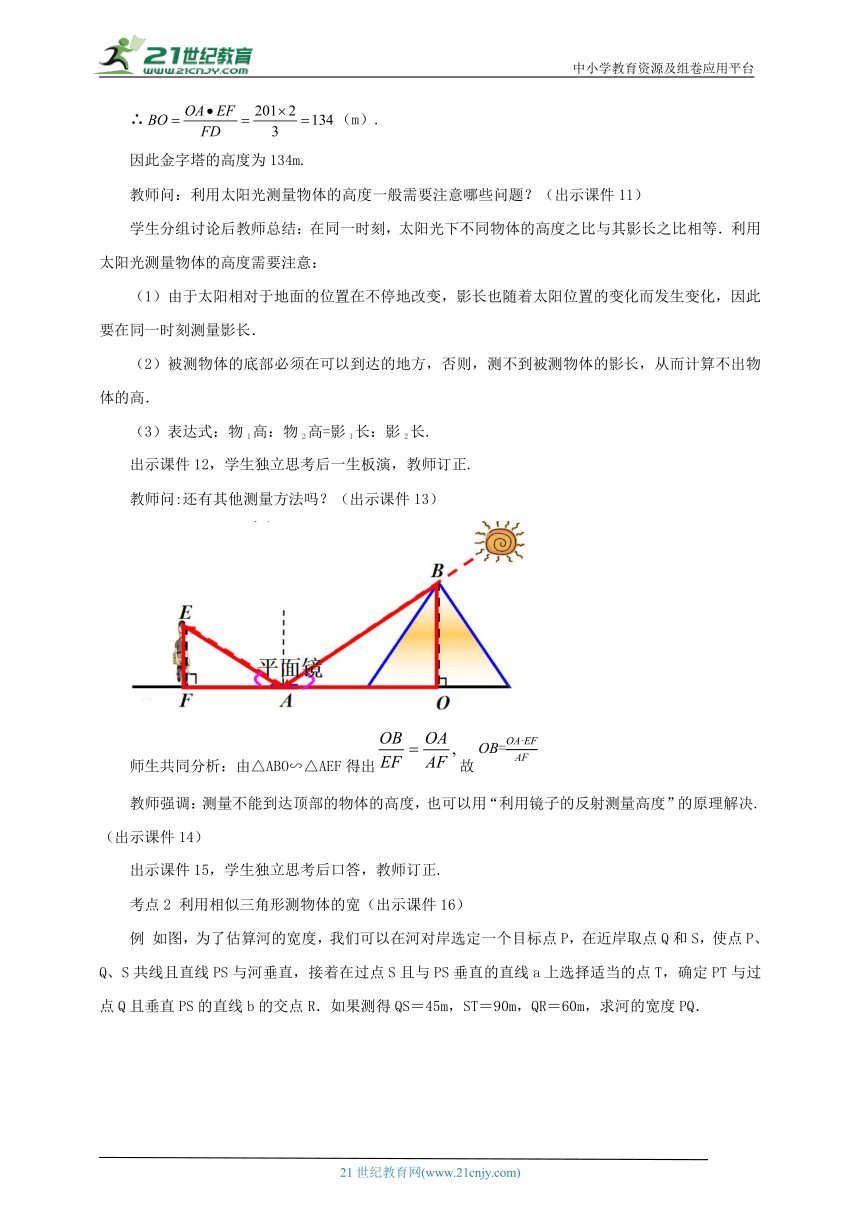
教师问:还有其他测量方法吗?(出示课件13)
师生共同分析:由△ABO∽△AEF得出故OB=
教师强调:测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.(出示课件14)
出示课件15,学生独立思考后口答,教师订正.
考点2 利用相似三角形测物体的宽(出示课件16)
例 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
学生独立思考后师生共同解决:
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST,
∴,
即,,PQ×90=(PQ+45)×60,
解得PQ=90(m).
因此,河宽大约为90m.
教师问:测量前面例题中的河宽,你还有哪些方法?(出示课件17)
学生分组讨论后教师强调:利用相似测量不能直接到达的两点间的距离,关键是构造相似三角形,构造的相似三角形可以为“A”字型,也可以为“X”字型,并测量出必要的数据,然后根据相似三角形的性质求出所要求的两点间的距离.该例题还可参照课本P41页练习2设计测量方案.
出示课件18,学生独立思考后一生板演,教师订正.
教师强调:测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.(出示课件19)
考点3 利用相似三角形测量有遮挡的物体
例 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m.一个人估计自己眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了?(出示课件20~21)
师生共同分析:如图(1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB、CD于点H、K.视线FA、FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域(盲区)之内.
解:如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树顶端点A、C恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD,
∴△AEH∽△CEK,
∴,
即,解得EH=8(m).
由此可知,如果观察者继续前进,当她与左边的树的距离小于8m时,由于这棵树的遮挡,她看不到右边树的顶端C.
教师问:利用相似来解决测量物体高度的问题的一般思路是怎样的 (出示课件22)
师生共同总结:一般情况下,可以从人眼所在的部位向物体作垂线,根据人、物体都与地面垂直构造相似三角形数学模型,利用相似三角形对应边的比相等解决问题.
出示课件23,学生独立思考后口答,教师订正.
(三)课堂练习(出示课件24-33)
教师引导学生练习24-33相应题目,巩固本课所学知识,约用时20分钟。
(四)课堂小结(出示课件34)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.在同一时刻,太阳光下不同物体的高度之比与其影长之比相等.利用太阳光测量物体的高度需要注意:
(1)由于太阳相对于地面的位置在不停地改变,影长也随着太阳位置的变化而发生变化,因此要在同一时刻测量影长.
(2)被测物体的底部必须在可以到达的地方,否则,测不到被测物体的影长,从而计算不出物体的高.
(3)表达式:物1高:物2高=影1长:影2长.
2.测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
3.利用相似测量不能直接到达的两点间的距离,关键是构造相似三角形,构造的相似三角形可以为“A”字型,也可以为“X”字型,并测量出必要的数据,然后根据相似三角形的性质求出所要求的两点间的距离.
4.利用相似来解决测量物体高度的问题的一般思路:一般情况下,可以从人眼所在的部位向物体作垂线,根据人、物体都与地面垂直构造相似三角形数学模型,利用相似三角形对应边的比相等解决问题.
(五)课前预习
预习下节课(27.3第1课时)的相关内容.
知道位似图形的定义、性质及画法.
七、课后作业
教材第41页练习第1题.
八、板书设计
27.2.3相似三角形应用举例
1.利用阳光下的影长解决实际问题
2.利用镜子的反射解决实际问题
3.利用标杆解决实际问题
九、教学反思
通过本节知识的学习,可以使学生综合运用三角形相似的判定和性质解决问题,发展学生的应用意识,加深学生对相似三角形的理解和认识.基本达到了预期的教学目标,大部分学生都学会了建立数学模型,利用相似的判定和性质来解决实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2 相似三角形
27.2.3相似三角形应用举例
一、教学目标
【知识与技能】
1.应用相似三角形的有关知识去解决简单的实际问题;
2.应用三角形相似的知识计算不能直接测量物体的长度和高度.
【过程与方法】
经历应用相似三角形的有关知识去解决简单的实际问题的全过程,培养学生的应用意识和把实际问题转化为数学问题并用数学方法去分析、解决实际问题的能力.
【情感态度与价值观】
1.通过著名的科学家如何测量神秘的金字塔的高度来激发学生学数学的兴趣,使全体学生积极参与探索,体验成功的喜悦;
2.力求培养学生科学,正确的数学观,体现探索精神.
二、课型
新授课
三、课时
1课时
四、教学重难点
【教学重点】
运用三角形相似的知识计算不能直接测量物体的长度和高度.
【教学难点】
通过审题、思考后,如何在实际问题中抽象出相似三角形的模型.
五、课前准备
教师:课件、直尺、三角板.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
教师问:在前面,我们学过哪些判定三角形相似的方法?相似三角形的性质是什么?
学生答:1.相似三角形的判定:
(1) 通过平行线;(2) 三边成比例;(3) 两边成比例且夹角相等;(4) 两角分别相等.
2.相似三角形的性质:
(1)对应边成比例,对应角相等;
(2)相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方.
教师问:观察下列图片,你会利用相似三角形知识解决一些不能直接测量的物体(如塔高、河宽等)的长度或高度的问题吗?
出示课件3~7,学生思考解决方法.
教师提示:利用相似三角形可以解决一些不能直接测量的物体的高度及两物之间的距离问题.(出示课件7)
(二)探索新知
知识点1 利用相似三角形测物体
古希腊数学家、天文学家泰勒斯利用相似三角形的原理,测量金字塔的高度.(出示课件9)
考点1 利用相似三角形测物体的高(出示课件10)
例 据史料记者,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.
如图,如果木杆EF长2m,它的影长FD为3m,测得OA为201m,求金字塔的高度BO.
师生共同分析:由于太阳离我们非常遥远,因此可以把太阳光近似的看成平行光线.
解:太阳光是平行光线,因此∠BAO=∠EDF,
又∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴,
∴(m).
因此金字塔的高度为134m.
教师问:利用太阳光测量物体的高度一般需要注意哪些问题?(出示课件11)
学生分组讨论后教师总结:在同一时刻,太阳光下不同物体的高度之比与其影长之比相等.利用太阳光测量物体的高度需要注意:
(1)由于太阳相对于地面的位置在不停地改变,影长也随着太阳位置的变化而发生变化,因此要在同一时刻测量影长.
(2)被测物体的底部必须在可以到达的地方,否则,测不到被测物体的影长,从而计算不出物体的高.
(3)表达式:物1高:物2高=影1长:影2长.
出示课件12,学生独立思考后一生板演,教师订正.
教师问:还有其他测量方法吗?(出示课件13)
师生共同分析:由△ABO∽△AEF得出故OB=
教师强调:测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.(出示课件14)
出示课件15,学生独立思考后口答,教师订正.
考点2 利用相似三角形测物体的宽(出示课件16)
例 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
学生独立思考后师生共同解决:
解:∵∠PQR=∠PST=90°,∠P=∠P,
∴△PQR∽△PST,
∴,
即,,PQ×90=(PQ+45)×60,
解得PQ=90(m).
因此,河宽大约为90m.
教师问:测量前面例题中的河宽,你还有哪些方法?(出示课件17)
学生分组讨论后教师强调:利用相似测量不能直接到达的两点间的距离,关键是构造相似三角形,构造的相似三角形可以为“A”字型,也可以为“X”字型,并测量出必要的数据,然后根据相似三角形的性质求出所要求的两点间的距离.该例题还可参照课本P41页练习2设计测量方案.
出示课件18,学生独立思考后一生板演,教师订正.
教师强调:测量如河宽等不易直接测量的物体的宽度,常构造相似三角形求解.(出示课件19)
考点3 利用相似三角形测量有遮挡的物体
例 已知左、右并排的两棵大树的高分别是AB=8m和CD=12m,两树底部的距离BD=5m.一个人估计自己眼睛距地面1.6m.她沿着正对这两棵树的一条水平直路l从左向右前进,当她与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C了?(出示课件20~21)
师生共同分析:如图(1),设观察者眼睛的位置为点F,画出观察者的水平视线FG,分别交AB、CD于点H、K.视线FA、FG的夹角∠AFH是观察点A时的仰角.类似地,∠CFK是观察点C时的仰角.由于树的遮挡,区域Ⅰ和Ⅱ都在观察者看不到的区域(盲区)之内.
解:如图(2),假设观察者从左向右走到点E时,她的眼睛的位置点E与两棵树顶端点A、C恰在一条直线上.
∵AB⊥l,CD⊥l,∴AB∥CD,
∴△AEH∽△CEK,
∴,
即,解得EH=8(m).
由此可知,如果观察者继续前进,当她与左边的树的距离小于8m时,由于这棵树的遮挡,她看不到右边树的顶端C.
教师问:利用相似来解决测量物体高度的问题的一般思路是怎样的 (出示课件22)
师生共同总结:一般情况下,可以从人眼所在的部位向物体作垂线,根据人、物体都与地面垂直构造相似三角形数学模型,利用相似三角形对应边的比相等解决问题.
出示课件23,学生独立思考后口答,教师订正.
(三)课堂练习(出示课件24-33)
教师引导学生练习24-33相应题目,巩固本课所学知识,约用时20分钟。
(四)课堂小结(出示课件34)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.在同一时刻,太阳光下不同物体的高度之比与其影长之比相等.利用太阳光测量物体的高度需要注意:
(1)由于太阳相对于地面的位置在不停地改变,影长也随着太阳位置的变化而发生变化,因此要在同一时刻测量影长.
(2)被测物体的底部必须在可以到达的地方,否则,测不到被测物体的影长,从而计算不出物体的高.
(3)表达式:物1高:物2高=影1长:影2长.
2.测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
3.利用相似测量不能直接到达的两点间的距离,关键是构造相似三角形,构造的相似三角形可以为“A”字型,也可以为“X”字型,并测量出必要的数据,然后根据相似三角形的性质求出所要求的两点间的距离.
4.利用相似来解决测量物体高度的问题的一般思路:一般情况下,可以从人眼所在的部位向物体作垂线,根据人、物体都与地面垂直构造相似三角形数学模型,利用相似三角形对应边的比相等解决问题.
(五)课前预习
预习下节课(27.3第1课时)的相关内容.
知道位似图形的定义、性质及画法.
七、课后作业
教材第41页练习第1题.
八、板书设计
27.2.3相似三角形应用举例
1.利用阳光下的影长解决实际问题
2.利用镜子的反射解决实际问题
3.利用标杆解决实际问题
九、教学反思
通过本节知识的学习,可以使学生综合运用三角形相似的判定和性质解决问题,发展学生的应用意识,加深学生对相似三角形的理解和认识.基本达到了预期的教学目标,大部分学生都学会了建立数学模型,利用相似的判定和性质来解决实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
