27.3 位似(第2课时)教案
图片预览

文档简介
中小学教育资源及组卷应用平台
27.3 位似
第2课时
一、教学目标
【知识与技能】
1.巩固位似图形及其有关概念.
2.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
【过程与方法】
通过学生动手操作,探究坐标的变化,类比平移,轴对称,旋转(中心对称)等变换,提高学生的动手能力和归纳问题的能力.
【情感态度与价值观】
1.让学生经历探究过程,体会数与形的联系,激发学生探究用坐标的变化规律来表示位似的兴趣.
2.渗透数形结合的数学思想,培养学生良好的学习习惯。
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
用图形的坐标的变化来表示图形的位似变换.
【教学难点】
把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、直尺、铅笔.
六、教学过程
(一)导入新课(出示课件2)
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
(二)探索新知
知识点1 平面直角坐标系中的位似变换
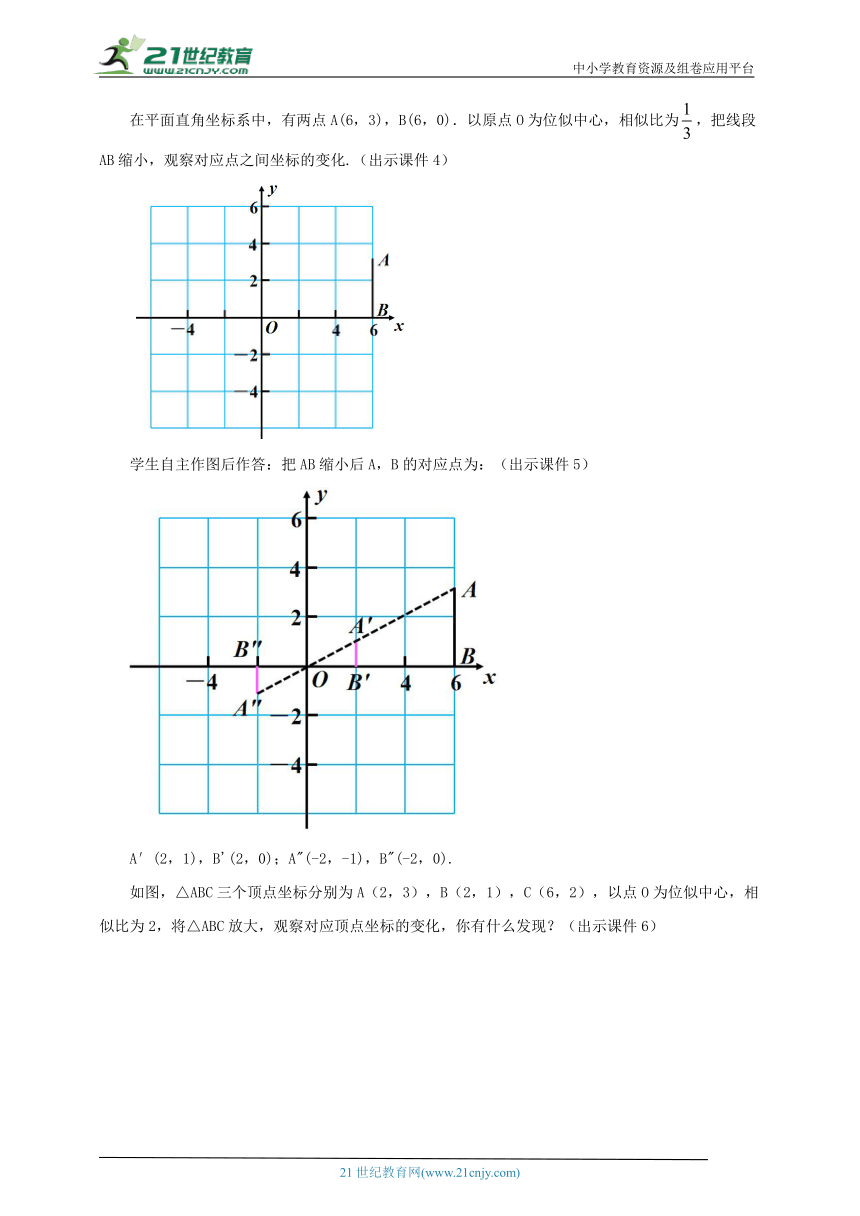
在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化.(出示课件4)
学生自主作图后作答:把AB缩小后A,B的对应点为:(出示课件5)
A′(2,1),B'(2,0);A"(-2,-1),B"(-2,0).
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?(出示课件6)
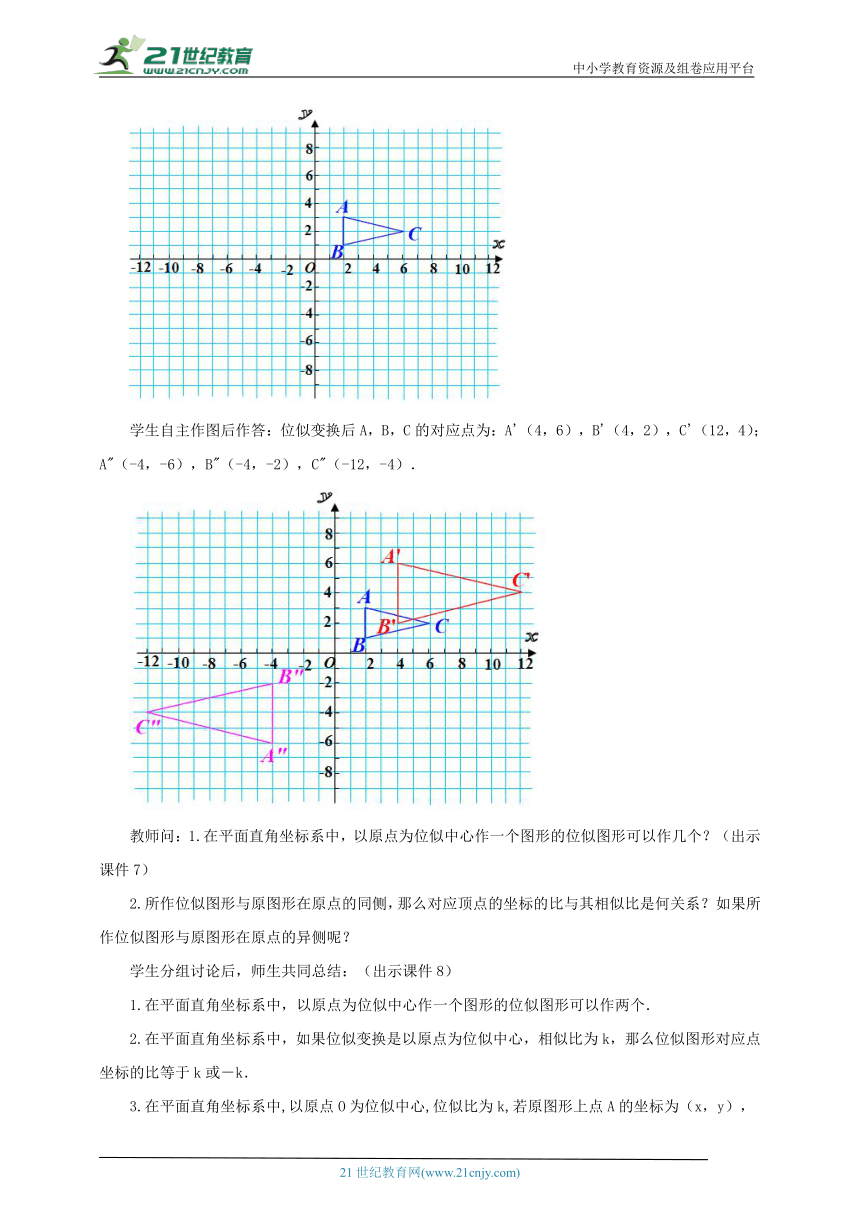
学生自主作图后作答:位似变换后A,B,C的对应点为:A'(4,6),B'(4,2),C'(12,4);A"(-4,-6),B"(-4,-2),C"(-12,-4).
教师问:1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?(出示课件7)
2.所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
学生分组讨论后,师生共同总结:(出示课件8)
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比等于k或-k.
3.在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A'的坐标为(kx,ky)或(-kx,-ky).
教师强调:当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的.
出示课件9,学生独立思考后口答,教师订正.
考点 利用平面直角坐标系中的位似变换作图
例 如图,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,画出一个三角形使它与△ABO的相似比为3:2.(出示课件10)
教师提示:画三角形关键是确定它各顶点的坐标.根据前面的归纳可知,点A的对应点A′的坐标为,即(-3,6),类似地,可以确定其他顶点的坐标.(出示课件11)
师生一起解答:
解:利用位似中对应点的坐标的变化规律,分别取点A′(-3,6),B′(-3,0),O(0,0).
顺次连接点A′,B′,O,所得的△A′B′O就是要画的一个图形.
教师问:还有其他画法吗?自己试一试.
学生尝试其他作法,教师加以指导.
出示课件12,学生独立解答,教师订正.
知识点2 平面直角坐标系中的图形变换
出示课件13,将图中的△ABC做下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴正向平移3个单位长度;
(2)关于x轴对称;
(3)以C为位似中心,将△ABC放大2倍;
(4)以C为中心,将△ABC顺时针旋转180°.
学生按要求作图后,教师用多媒体加以展示.
教师问:截止现在,你总共学了哪些图形变换?它们有何异同点?
学生分组讨论后,师生共同总结:(出示课件14)
名称 规律 变换方式
平移 对应点的横坐标或纵坐标加上(或减去)平移的单位长度. 全等变换
轴对称 以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数; 以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数.
旋转 若一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数.
位似 当以原点为位似中心时,变换前后两个图形对应点的同名坐标之比的绝对值等于相似比. 相似变换
出示课件15、16,学生独立解答,教师订正.
(三)课堂练习(出示课件17-26)
练习课件17-26相应题目,巩固本课知识点,约用时15分钟。
(四)课堂小结(出示课件27)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比等于k或-k.
3.在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A'的坐标为(kx,ky)或(-kx,-ky).
(五)课前预习
预习下节课(28.1第1课时)的相关内容.
知道正弦的意义,能用正弦的定义解决简单的问题.
课后作业
教材第50页练习第2题.
板书设计
27.3位似(第2课时)
1.平面直角坐标系中的位似变换
2.平面直角坐标系中的图形变换
3.例题:
教学反思
这节课主要是让学生感受在平面直角坐标系中的位似图形根据坐标的变化而变化,教学过程中要提高学生学习积极性,使心情愉悦、思维活跃,这样才能真正激发学生学习数学的兴趣,提高课堂学习效率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.3 位似
第2课时
一、教学目标
【知识与技能】
1.巩固位似图形及其有关概念.
2.会用图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
【过程与方法】
通过学生动手操作,探究坐标的变化,类比平移,轴对称,旋转(中心对称)等变换,提高学生的动手能力和归纳问题的能力.
【情感态度与价值观】
1.让学生经历探究过程,体会数与形的联系,激发学生探究用坐标的变化规律来表示位似的兴趣.
2.渗透数形结合的数学思想,培养学生良好的学习习惯。
二、课型
新授课
三、课时
第1课时 共2课时
四、教学重难点
【教学重点】
用图形的坐标的变化来表示图形的位似变换.
【教学难点】
把一个图形按一定大小比例放大或缩小后,点的坐标变化的规律.
五、课前准备
教师:课件、三角尺、直尺等.
学生:三角尺、直尺、铅笔.
六、教学过程
(一)导入新课(出示课件2)
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么,位似是否也可以用两个图形坐标之间的关系来表示呢?
(二)探索新知
知识点1 平面直角坐标系中的位似变换
在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为,把线段AB缩小,观察对应点之间坐标的变化.(出示课件4)
学生自主作图后作答:把AB缩小后A,B的对应点为:(出示课件5)
A′(2,1),B'(2,0);A"(-2,-1),B"(-2,0).
如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?(出示课件6)
学生自主作图后作答:位似变换后A,B,C的对应点为:A'(4,6),B'(4,2),C'(12,4);A"(-4,-6),B"(-4,-2),C"(-12,-4).
教师问:1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?(出示课件7)
2.所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
学生分组讨论后,师生共同总结:(出示课件8)
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比等于k或-k.
3.在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A'的坐标为(kx,ky)或(-kx,-ky).
教师强调:当k>1时,图形扩大为原来的k倍;当0<k<1时,图形缩小为原来的.
出示课件9,学生独立思考后口答,教师订正.
考点 利用平面直角坐标系中的位似变换作图
例 如图,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,画出一个三角形使它与△ABO的相似比为3:2.(出示课件10)
教师提示:画三角形关键是确定它各顶点的坐标.根据前面的归纳可知,点A的对应点A′的坐标为,即(-3,6),类似地,可以确定其他顶点的坐标.(出示课件11)
师生一起解答:
解:利用位似中对应点的坐标的变化规律,分别取点A′(-3,6),B′(-3,0),O(0,0).
顺次连接点A′,B′,O,所得的△A′B′O就是要画的一个图形.
教师问:还有其他画法吗?自己试一试.
学生尝试其他作法,教师加以指导.
出示课件12,学生独立解答,教师订正.
知识点2 平面直角坐标系中的图形变换
出示课件13,将图中的△ABC做下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴正向平移3个单位长度;
(2)关于x轴对称;
(3)以C为位似中心,将△ABC放大2倍;
(4)以C为中心,将△ABC顺时针旋转180°.
学生按要求作图后,教师用多媒体加以展示.
教师问:截止现在,你总共学了哪些图形变换?它们有何异同点?
学生分组讨论后,师生共同总结:(出示课件14)
名称 规律 变换方式
平移 对应点的横坐标或纵坐标加上(或减去)平移的单位长度. 全等变换
轴对称 以x轴为对称轴,则对应点的横坐标相等,纵坐标互为相反数; 以y轴为对称轴,则对应点的纵坐标相等,横坐标互为相反数.
旋转 若一个图形绕原点旋转180°,则旋转前后两个图形对应点的横坐标与纵坐标都互为相反数.
位似 当以原点为位似中心时,变换前后两个图形对应点的同名坐标之比的绝对值等于相似比. 相似变换
出示课件15、16,学生独立解答,教师订正.
(三)课堂练习(出示课件17-26)
练习课件17-26相应题目,巩固本课知识点,约用时15分钟。
(四)课堂小结(出示课件27)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个.
2.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点坐标的比等于k或-k.
3.在平面直角坐标系中,以原点O为位似中心,位似比为k,若原图形上点A的坐标为(x,y),那么位似图形对应点A'的坐标为(kx,ky)或(-kx,-ky).
(五)课前预习
预习下节课(28.1第1课时)的相关内容.
知道正弦的意义,能用正弦的定义解决简单的问题.
课后作业
教材第50页练习第2题.
板书设计
27.3位似(第2课时)
1.平面直角坐标系中的位似变换
2.平面直角坐标系中的图形变换
3.例题:
教学反思
这节课主要是让学生感受在平面直角坐标系中的位似图形根据坐标的变化而变化,教学过程中要提高学生学习积极性,使心情愉悦、思维活跃,这样才能真正激发学生学习数学的兴趣,提高课堂学习效率.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
