28.2.2 应用举例(第1课时)教案
图片预览


文档简介
中小学教育资源及组卷应用平台
28.2 解直角三角形及其应用
28.2.2 应用举例(第1课时)
一、教学目标
【知识与技能】
1.巩固解直角三角形相关知识;
2.能从实际问题中构造直角三角形,会把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题.
【过程与方法】
经历解直角三角形的实际应用,运用转化思想,学会把实际问题转化为数学问题来解决,培养学生分析问题、解决问题的能力.
【情感态度与价值观】
渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识.
二、课型
新授课
三、课时
第1课时 共3课时
四、教学重难点
【教学重点】
能利用直角三角形元素之间的关系,解决实际问题.
【教学难点】
实际问题转化为数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
高跟鞋深受很多女性的喜爱,但有时候,如果鞋跟太高,也有可能“喜剧”变“悲剧”.
你知道高跟鞋的鞋底与地面的夹角为多少度时,人脚的感觉最舒适吗?
(二)探索新知
知识点 利用解直角三角形解答简单的问题(出示课件4)
解直角三角形主要用到以下知识:
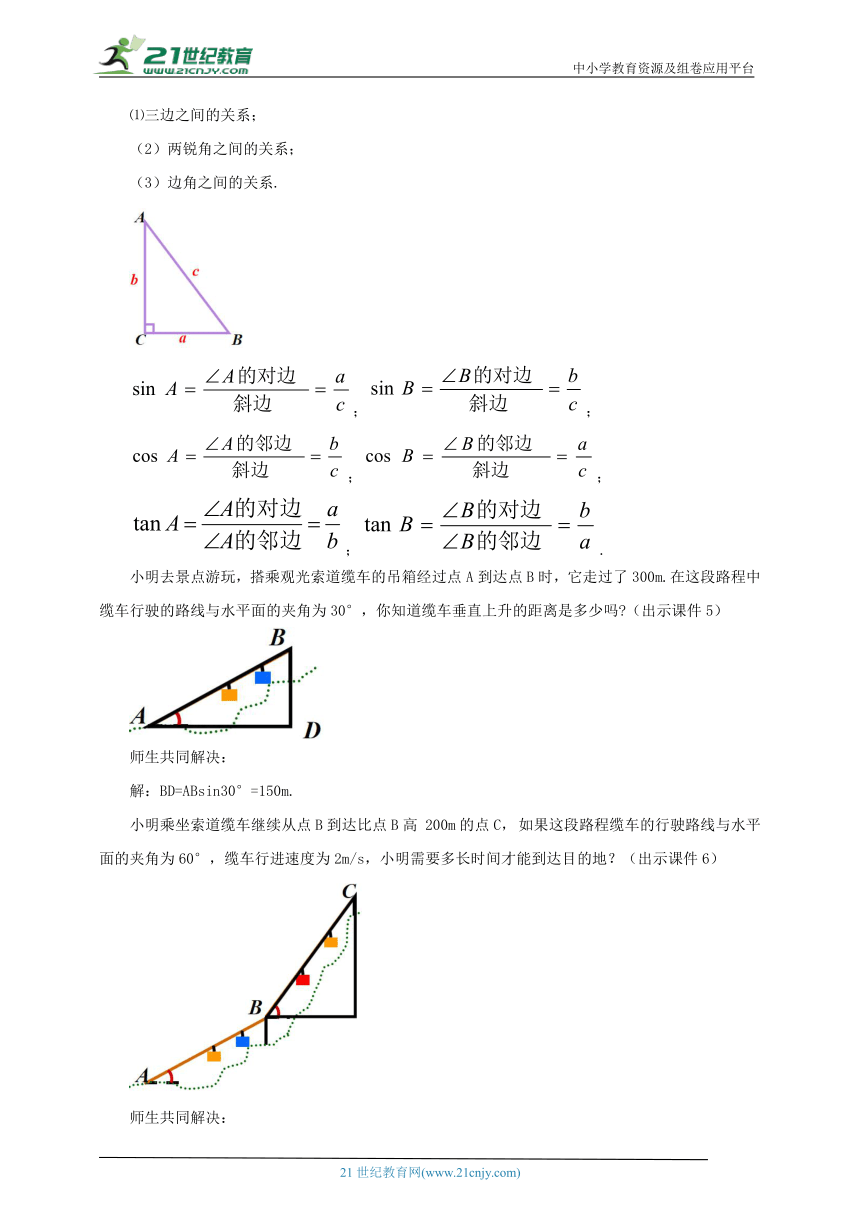
⑴三边之间的关系;
(2)两锐角之间的关系;
(3)边角之间的关系.
;;
;;
;.
小明去景点游玩,搭乘观光索道缆车的吊箱经过点A到达点B时,它走过了300m.在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗 (出示课件5)
师生共同解决:
解:BD=ABsin30°=150m.
小明乘坐索道缆车继续从点B到达比点B高 200m的点C, 如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为2m/s,小明需要多长时间才能到达目的地?(出示课件6)
师生共同解决:
解:
231÷2=115.5(s),
小明需要115.5s才能到达目的地.
考点1 建立直角三角形模型解答简单的问题.
例 2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行.如图,当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?(出示课件7~8)
教师分析:从组合体中能直接看到的地球表面最远点,是视线与地球相切的切点.求最远点与P点的距离就是求弧PQ的长.为计算弧PQ的长,必须要求出∠POQ的度数.
解:设∠FOQ =α,FQ是⊙O切线,△FOQ是直角三角形.
∵,
∴a≈18.36°
.
当组合体在P点的正上方时,从中观测地球表面时的最远点距离P点约2051km.
教师问:从前面的例题解答中,你能体会到解直角三角形的应用前提条件是什么吗?如何进行?(出示课件9)
学生分组讨论后,教师强调:一般情况下,直角三角形是求解或运用三角函数值的前提条件,故当题目中提供的并非直角三角形时,需添加辅助线构造直角三角形,然后运用三角函数解决问题.
师生共同总结:(出示课件10)
解直角三角形的应用:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;
(3)得到数学问题答案;
(4)得到实际问题答案.
教师强调:数学问题的解符合实际意义才可以成为实际问题的解.
出示课件11,学生独立解决,一生板演,教师订正.
考点2 建立直角三角形模型解答生活问题.
例 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?(出示课件12~13)
师生共同分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:已知DE=0.5m,AD=AB=3m,∠DAB=60°,△ACB为直角三角形,求CE的长度.
师生共同解决:(出示课件14)
解:∵∠CAB=60°,AD=AB=3m,
∴AC=ABcos∠CAB=1.5m.
∴CD=AD-AC=1.5m.
∴CE=CD+DE=2.0m.
即秋千踏板与地面的最大距离为2.0m.
出示课件15~16,学生独立解决,一生板演,教师订正.
(三)课堂练习(出示课件17-25)
引导学生练习课件17-25页题目,解决相应问题,约用时20分钟
(四)课堂小结(出示课件26)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
解直角三角形的应用:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;
(3)得到数学问题答案;
(4)得到实际问题答案.
(五)课前预习
预习下节课(28.2.2(第2课时))的相关内容.
会解简单的仰角、俯角问题.
课后作业
教材第76页练习第2题.
板书设计
28.2.2 应用举例(第1课时)
1.简单应用
2.例题
九、教学反思
本节课为了充分发挥学生的主观能动性,可引导学生通过小组讨论,大胆地发表意见,提高学生学习数学的兴趣.能够使学生自己构造实际问题中的直角三角形模型,并通过解直角三角形解决实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.2 解直角三角形及其应用
28.2.2 应用举例(第1课时)
一、教学目标
【知识与技能】
1.巩固解直角三角形相关知识;
2.能从实际问题中构造直角三角形,会把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题.
【过程与方法】
经历解直角三角形的实际应用,运用转化思想,学会把实际问题转化为数学问题来解决,培养学生分析问题、解决问题的能力.
【情感态度与价值观】
渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识.
二、课型
新授课
三、课时
第1课时 共3课时
四、教学重难点
【教学重点】
能利用直角三角形元素之间的关系,解决实际问题.
【教学难点】
实际问题转化为数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
高跟鞋深受很多女性的喜爱,但有时候,如果鞋跟太高,也有可能“喜剧”变“悲剧”.
你知道高跟鞋的鞋底与地面的夹角为多少度时,人脚的感觉最舒适吗?
(二)探索新知
知识点 利用解直角三角形解答简单的问题(出示课件4)
解直角三角形主要用到以下知识:
⑴三边之间的关系;
(2)两锐角之间的关系;
(3)边角之间的关系.
;;
;;
;.
小明去景点游玩,搭乘观光索道缆车的吊箱经过点A到达点B时,它走过了300m.在这段路程中缆车行驶的路线与水平面的夹角为30°,你知道缆车垂直上升的距离是多少吗 (出示课件5)
师生共同解决:
解:BD=ABsin30°=150m.
小明乘坐索道缆车继续从点B到达比点B高 200m的点C, 如果这段路程缆车的行驶路线与水平面的夹角为60°,缆车行进速度为2m/s,小明需要多长时间才能到达目的地?(出示课件6)
师生共同解决:
解:
231÷2=115.5(s),
小明需要115.5s才能到达目的地.
考点1 建立直角三角形模型解答简单的问题.
例 2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行.如图,当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?(出示课件7~8)
教师分析:从组合体中能直接看到的地球表面最远点,是视线与地球相切的切点.求最远点与P点的距离就是求弧PQ的长.为计算弧PQ的长,必须要求出∠POQ的度数.
解:设∠FOQ =α,FQ是⊙O切线,△FOQ是直角三角形.
∵,
∴a≈18.36°
.
当组合体在P点的正上方时,从中观测地球表面时的最远点距离P点约2051km.
教师问:从前面的例题解答中,你能体会到解直角三角形的应用前提条件是什么吗?如何进行?(出示课件9)
学生分组讨论后,教师强调:一般情况下,直角三角形是求解或运用三角函数值的前提条件,故当题目中提供的并非直角三角形时,需添加辅助线构造直角三角形,然后运用三角函数解决问题.
师生共同总结:(出示课件10)
解直角三角形的应用:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;
(3)得到数学问题答案;
(4)得到实际问题答案.
教师强调:数学问题的解符合实际意义才可以成为实际问题的解.
出示课件11,学生独立解决,一生板演,教师订正.
考点2 建立直角三角形模型解答生活问题.
例 如图,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为60°,则秋千踏板与地面的最大距离为多少?(出示课件12~13)
师生共同分析:根据题意,可知秋千踏板与地面的最大距离为CE的长度.因此,本题可抽象为:已知DE=0.5m,AD=AB=3m,∠DAB=60°,△ACB为直角三角形,求CE的长度.
师生共同解决:(出示课件14)
解:∵∠CAB=60°,AD=AB=3m,
∴AC=ABcos∠CAB=1.5m.
∴CD=AD-AC=1.5m.
∴CE=CD+DE=2.0m.
即秋千踏板与地面的最大距离为2.0m.
出示课件15~16,学生独立解决,一生板演,教师订正.
(三)课堂练习(出示课件17-25)
引导学生练习课件17-25页题目,解决相应问题,约用时20分钟
(四)课堂小结(出示课件26)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
解直角三角形的应用:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形;
(3)得到数学问题答案;
(4)得到实际问题答案.
(五)课前预习
预习下节课(28.2.2(第2课时))的相关内容.
会解简单的仰角、俯角问题.
课后作业
教材第76页练习第2题.
板书设计
28.2.2 应用举例(第1课时)
1.简单应用
2.例题
九、教学反思
本节课为了充分发挥学生的主观能动性,可引导学生通过小组讨论,大胆地发表意见,提高学生学习数学的兴趣.能够使学生自己构造实际问题中的直角三角形模型,并通过解直角三角形解决实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
