28.2.2 应用举例(第2课时)教案
图片预览


文档简介
中小学教育资源及组卷应用平台
28.2 解直角三角形及其应用
28.2.2 应用举例(第2课时)
一、教学目标
【知识与技能】
1.使学生了解仰角、俯角的概念,并能够根据直角三角形的知识解决实际问题;
2.进一步掌握用解直角三角形的知识解决实际问题的方法.
【过程与方法】
注重由已知到未知的探索发现过程,通过温故知新部分进行承前启后,让学生感悟知识的形成与发展过程,由简单到复杂,由已知到未知,由具体到抽象,渗透分类讨论、数形结合、用字母表示数、化归等数学思想和方法.
【情感态度与价值观】
体现数学与现实的联系,激发学生学习数学的主动性,通过小组交流合作,提高学生的交往能力,提高团队合作精神.
二、课型
新授课
三、课时
第2课时 共3课时
四、教学重难点
【教学重点】
用仰角、俯角等概念解决实际问题.
【教学难点】
实际问题转化为数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
㈠导入新课(出示课件2)
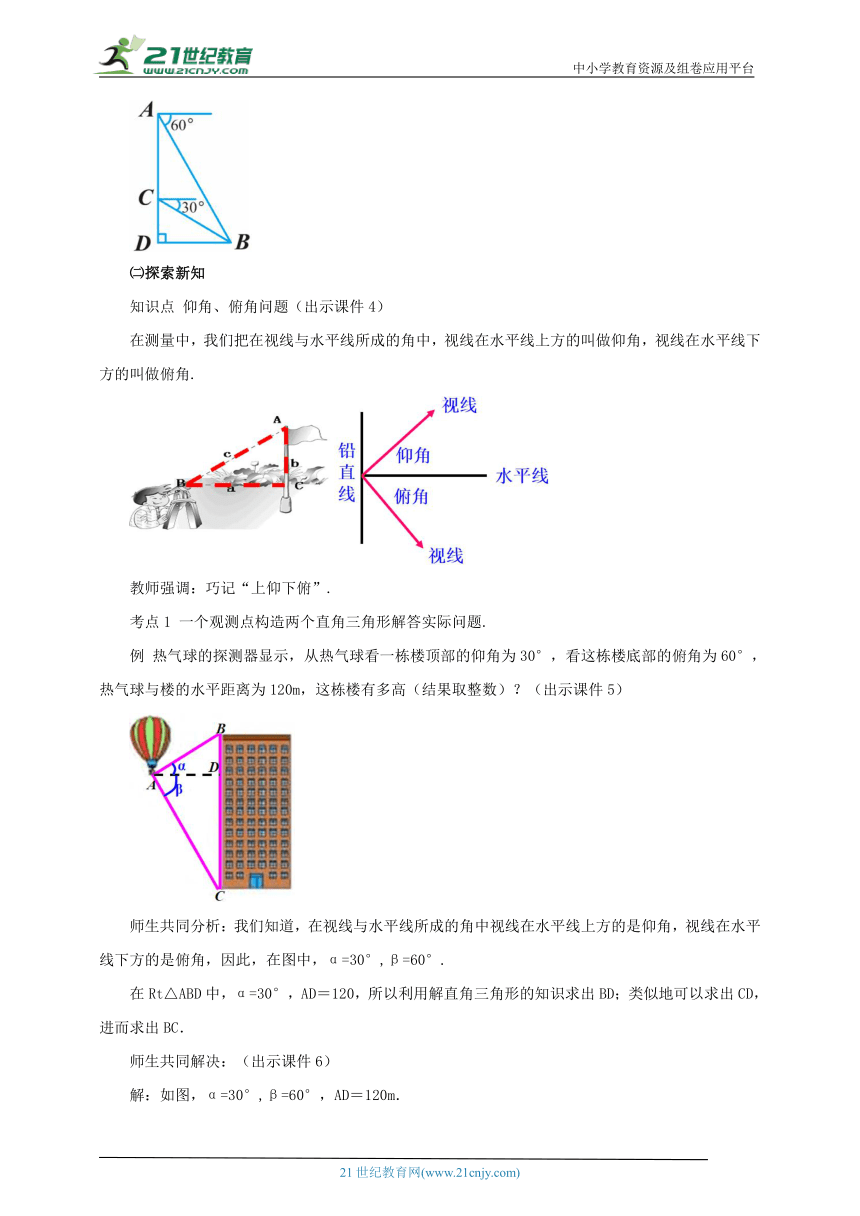
如图所示,一只猫在窝顶A处测得老鼠所在地B处的俯角为60°,然后下到猫窝的C处,测得B处的俯角为30°.已知AC =40 m,若这只猫以 5 m/s的速度从猫窝底部D处出发,几秒钟后能抓到老鼠 (结果精确到个位)(假设老鼠不动)
㈡探索新知
知识点 仰角、俯角问题(出示课件4)
在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角,视线在水平线下方的叫做俯角.
教师强调:巧记“上仰下俯”.
考点1 一个观测点构造两个直角三角形解答实际问题.
例 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?(出示课件5)
师生共同分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.
在Rt△ABD中,α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
师生共同解决:(出示课件6)
解:如图,α=30°,β=60°,AD=120m.
(m).
答:这栋楼高约为277m.
师生共同总结:(出示课件7)
解决与仰角、俯角有关的实际问题的方法:
根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形使问题获解.
出示课件8,学生独立解决并口答,教师订正.
考点2 两个观测点构造两个直角三角形解答实际问题.
例2 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45°,求飞机的高度 .(结果取整数.参考数据:sin37°≈0.6,cos37 °≈0.8,tan37°≈0.75)(出示课件9)
生独立思考后师生共同解决:(出示课件10)
解:作PO⊥AB交AB的延长线于O.
设PO=x米,
在Rt△POB中,∠PBO=45°,OB=PO= x米.
在Rt△POA中,∠PAB=37°,
即解得x=1200.
故飞机的高度为1200米.
出示课件11~12,学生独立解决,一生板演,教师订正.
(三)课堂练习(出示课件13-20)
引导学生练习课件13-20对应题目,约用时20分钟。
(四)课堂小结(出示课件21)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
解决有关仰角,俯角的实际问题的方法:
⑴仰角和俯角是指视线与水平线的夹角,上仰下俯.
⑵解答有关仰角俯角的问题关键是弄清仰角和俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
⑶若有两个或两个以上的三角形,不能直接解出的,可以考虑分别由两个三角形找出含有相同未知元素的关系式,运用方程知识求解.
(五)课前预习
预习下节课(28.2.2(第3课时))的相关内容.
会解简单的方向角、坡度问题.
课后作业
教材第79页练习第8题.
板书设计
28.2.2 应用举例(第2课时)
1.仰角、俯角
2.例题
九、教学反思
本节课尽可能站在学生的角度上思考问题,设计好教学过程中的每一个细节.让学生更多地参与到课堂的教学过程中,让学生体验思考的过程,体验成功的喜悦和失败的挫折,舍得把课堂让给学生,让学生做课堂这个小小舞台的主角.使课堂更加鲜活,充满人性魅力,课堂教学效率较高.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.2 解直角三角形及其应用
28.2.2 应用举例(第2课时)
一、教学目标
【知识与技能】
1.使学生了解仰角、俯角的概念,并能够根据直角三角形的知识解决实际问题;
2.进一步掌握用解直角三角形的知识解决实际问题的方法.
【过程与方法】
注重由已知到未知的探索发现过程,通过温故知新部分进行承前启后,让学生感悟知识的形成与发展过程,由简单到复杂,由已知到未知,由具体到抽象,渗透分类讨论、数形结合、用字母表示数、化归等数学思想和方法.
【情感态度与价值观】
体现数学与现实的联系,激发学生学习数学的主动性,通过小组交流合作,提高学生的交往能力,提高团队合作精神.
二、课型
新授课
三、课时
第2课时 共3课时
四、教学重难点
【教学重点】
用仰角、俯角等概念解决实际问题.
【教学难点】
实际问题转化为数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
㈠导入新课(出示课件2)
如图所示,一只猫在窝顶A处测得老鼠所在地B处的俯角为60°,然后下到猫窝的C处,测得B处的俯角为30°.已知AC =40 m,若这只猫以 5 m/s的速度从猫窝底部D处出发,几秒钟后能抓到老鼠 (结果精确到个位)(假设老鼠不动)
㈡探索新知
知识点 仰角、俯角问题(出示课件4)
在测量中,我们把在视线与水平线所成的角中,视线在水平线上方的叫做仰角,视线在水平线下方的叫做俯角.
教师强调:巧记“上仰下俯”.
考点1 一个观测点构造两个直角三角形解答实际问题.
例 热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120m,这栋楼有多高(结果取整数)?(出示课件5)
师生共同分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.
在Rt△ABD中,α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
师生共同解决:(出示课件6)
解:如图,α=30°,β=60°,AD=120m.
(m).
答:这栋楼高约为277m.
师生共同总结:(出示课件7)
解决与仰角、俯角有关的实际问题的方法:
根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形使问题获解.
出示课件8,学生独立解决并口答,教师订正.
考点2 两个观测点构造两个直角三角形解答实际问题.
例2 如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45°,求飞机的高度 .(结果取整数.参考数据:sin37°≈0.6,cos37 °≈0.8,tan37°≈0.75)(出示课件9)
生独立思考后师生共同解决:(出示课件10)
解:作PO⊥AB交AB的延长线于O.
设PO=x米,
在Rt△POB中,∠PBO=45°,OB=PO= x米.
在Rt△POA中,∠PAB=37°,
即解得x=1200.
故飞机的高度为1200米.
出示课件11~12,学生独立解决,一生板演,教师订正.
(三)课堂练习(出示课件13-20)
引导学生练习课件13-20对应题目,约用时20分钟。
(四)课堂小结(出示课件21)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
解决有关仰角,俯角的实际问题的方法:
⑴仰角和俯角是指视线与水平线的夹角,上仰下俯.
⑵解答有关仰角俯角的问题关键是弄清仰角和俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.
⑶若有两个或两个以上的三角形,不能直接解出的,可以考虑分别由两个三角形找出含有相同未知元素的关系式,运用方程知识求解.
(五)课前预习
预习下节课(28.2.2(第3课时))的相关内容.
会解简单的方向角、坡度问题.
课后作业
教材第79页练习第8题.
板书设计
28.2.2 应用举例(第2课时)
1.仰角、俯角
2.例题
九、教学反思
本节课尽可能站在学生的角度上思考问题,设计好教学过程中的每一个细节.让学生更多地参与到课堂的教学过程中,让学生体验思考的过程,体验成功的喜悦和失败的挫折,舍得把课堂让给学生,让学生做课堂这个小小舞台的主角.使课堂更加鲜活,充满人性魅力,课堂教学效率较高.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
