28.2.2 应用举例(第3课时)教案
图片预览



文档简介
中小学教育资源及组卷应用平台
28.2 解直角三角形及其应用
28.2.2 应用举例(第3课时)
一、教学目标
【知识与技能】
1.正确理解方向角、坡度、坡角的概念;
2.能运用解直角三角形知识解决方向角、坡度的问题;
3.能够解决与解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等.
【过程与方法】
通过实际问题的求解,总结出用解直角三角形的知识解决问题的一般过程,增强分析问题和解决问题的能力。
【情感态度与价值观】
渗透数形结合的思想方法,增强学生的数学应用意识和能力.
二、课型
新授课
三、课时
第3课时 共3课时
四、教学重难点
【教学重点】
用三角函数有关知识解决方位角问题.
【教学难点】
学会准确分析问题并将实际问题转化成数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
宜宾是国家级历史文化名城,大观楼是其标志性建筑之一
(如图①).喜爱数学的小伟决定用所学的知识测量大观楼的高度,如图②所示,他站在点B处利用测角仪测得大观楼最高点P的仰角为45°,又前进了12 m到达点A处,测得点P的仰角为60°.请你帮助小伟算一算大观楼的高度(测角仪的高度忽略不计,结果保留整数).
(二)探索新知
知识点1 方向角的有关问题(出示课件4)
方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角.
教师强调:(出示课件5)
(1)因为方向角是指北或指南方向线与目标方向线所成的角,所以方向角通常都写成“北偏……”,“南偏……”,的形式.
(2)解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.
(3)观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助于此性质进行角度转换.
考点1 有关方向角的实际问题——距离.(出示课件6)
例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
学生独立思考后师生共同解决:(出示课件7)
解:如图,在Rt△APC中,PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
教师强调:利用解直角三角形的知识解决实际问题的一般过程是:(出示课件8)
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
出示课件9,学生独立解决,一生板演,教师订正.
考点2 有关方向角的实际问题——预测路线.(出示课件10)
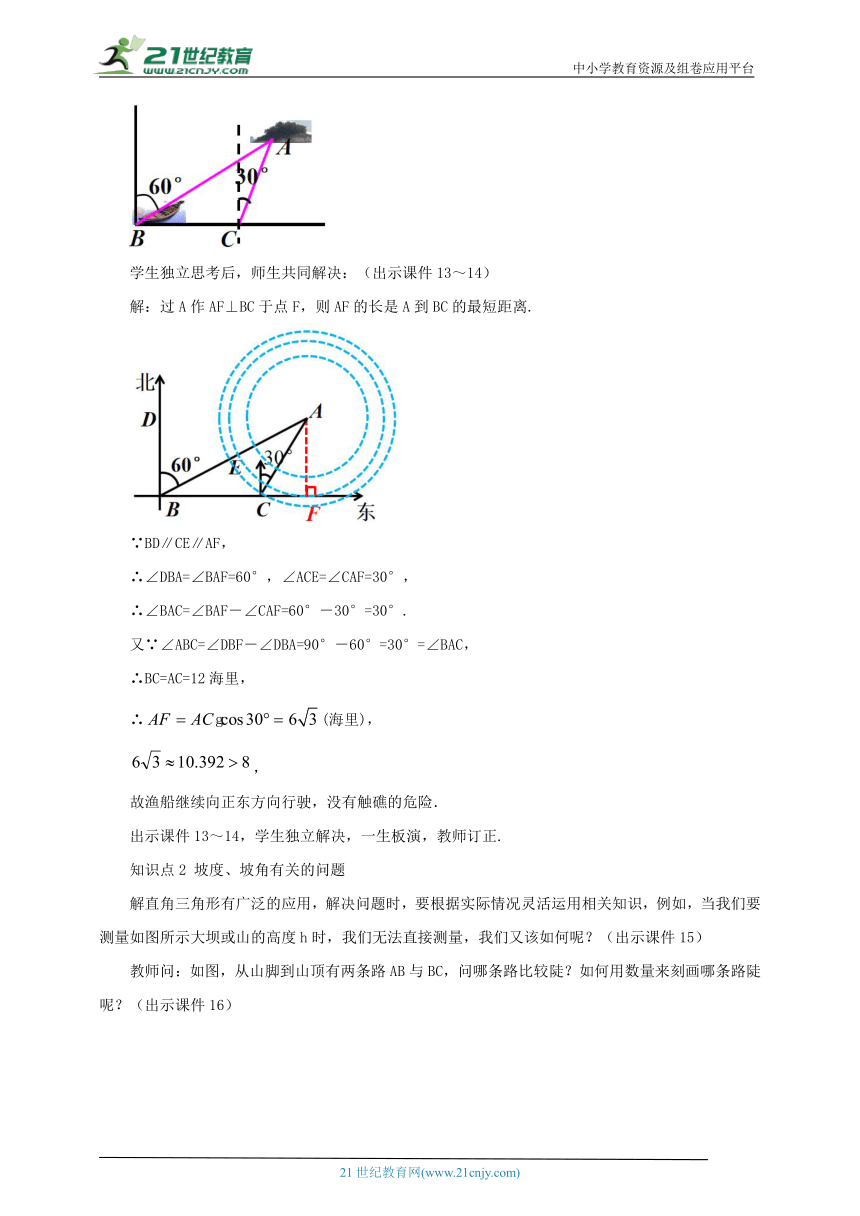
例 海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
学生独立思考后,师生共同解决:(出示课件13~14)
解:过A作AF⊥BC于点F,则AF的长是A到BC的最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF=60°-30°=30°.
又∵∠ABC=∠DBF-∠DBA=90°-60°=30°=∠BAC,
∴BC=AC=12海里,
∴(海里),
,
故渔船继续向正东方向行驶,没有触礁的危险.
出示课件13~14,学生独立解决,一生板演,教师订正.
知识点2 坡度、坡角有关的问题
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,我们无法直接测量,我们又该如何呢?(出示课件15)
教师问:如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?如何用数量来刻画哪条路陡呢?(出示课件16)
学生思考后,师生共同总结:(出示课件17)
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,如图,坡度通常写成的形式.
教师强调:坡度越大,坡角越大,坡面越陡.
出示课件18,学生独立解决并口答,教师订正.
考点1 利用坡度、坡角解答大坝问题
例 如图,防洪大堤的横截面是梯形 ABCD,其中AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)(出示课件19)
学生独立思考后,师生共同解答:(出示课件20)
解:过点A作AF⊥BC于点F,
在Rt△ABF中,∠ABF=∠α=60°,
则AF=AB·sin60°=(m),
在Rt△AEF中,∠E=∠β=45°,则(m).
故改造后的坡长AE为m.
出示课件21~22,学生独立解决,一生板演,教师订正.
考点2 利用坡度、坡角解答山坡问题
例 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?(出示课件23)
学生独立思考后,师生共同解答:(出示课件24)
解:用α表示坡角的大小,由题意可得
因此α≈26.57°.
在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,
因此
从而BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3m.
出示课件25,学生独立解决,教师订正.
(三)课堂练习(出示课件26-36)
练习课件26-36页题目,巩固所学知识点,约用时20分钟。
(四)课堂小结(出示课件21)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角.
2.坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
3.坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示.
4.坡度越大,坡角越大,坡面越陡.
(五)课前预习
预习下节课(29.1(第1课时))的相关内容.
知道什么是投影、平行投影及中心投影.
课后作业
教材第77页练习第2题.
板书设计
28.2.2 应用举例(第3课时)
1.方向角的意义;
2.坡度、坡角的意义;
3.例题
九、教学反思
将解直角三角形应用到实际生活中,有利于培养学生的空间想象能力,即要求学生通过对实物的观察或根据文字语言中的某些条件,画出适合他们的图形.这一方面在教学过程应由学生展开,并留给学生思考的时间,给学生充分的自主思考空间和时间,让学生积极主动地学习.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.2 解直角三角形及其应用
28.2.2 应用举例(第3课时)
一、教学目标
【知识与技能】
1.正确理解方向角、坡度、坡角的概念;
2.能运用解直角三角形知识解决方向角、坡度的问题;
3.能够解决与解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等.
【过程与方法】
通过实际问题的求解,总结出用解直角三角形的知识解决问题的一般过程,增强分析问题和解决问题的能力。
【情感态度与价值观】
渗透数形结合的思想方法,增强学生的数学应用意识和能力.
二、课型
新授课
三、课时
第3课时 共3课时
四、教学重难点
【教学重点】
用三角函数有关知识解决方位角问题.
【教学难点】
学会准确分析问题并将实际问题转化成数学模型.
五、课前准备
教师:课件、直尺、三角板等.
学生:直尺、三角板.
六、教学过程
(一)导入新课(出示课件2)
宜宾是国家级历史文化名城,大观楼是其标志性建筑之一
(如图①).喜爱数学的小伟决定用所学的知识测量大观楼的高度,如图②所示,他站在点B处利用测角仪测得大观楼最高点P的仰角为45°,又前进了12 m到达点A处,测得点P的仰角为60°.请你帮助小伟算一算大观楼的高度(测角仪的高度忽略不计,结果保留整数).
(二)探索新知
知识点1 方向角的有关问题(出示课件4)
方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角.
教师强调:(出示课件5)
(1)因为方向角是指北或指南方向线与目标方向线所成的角,所以方向角通常都写成“北偏……”,“南偏……”,的形式.
(2)解决实际问题时,可利用正南、正北、正西、正东方向线构造直角三角形来求解.
(3)观测点不同,所得的方向角也不同,但各个观测点的南北方向线是互相平行的,通常借助于此性质进行角度转换.
考点1 有关方向角的实际问题——距离.(出示课件6)
例 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(结果取整数)?
学生独立思考后师生共同解决:(出示课件7)
解:如图,在Rt△APC中,PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile.
教师强调:利用解直角三角形的知识解决实际问题的一般过程是:(出示课件8)
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
出示课件9,学生独立解决,一生板演,教师订正.
考点2 有关方向角的实际问题——预测路线.(出示课件10)
例 海中有一个小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达C点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
学生独立思考后,师生共同解决:(出示课件13~14)
解:过A作AF⊥BC于点F,则AF的长是A到BC的最短距离.
∵BD∥CE∥AF,
∴∠DBA=∠BAF=60°,∠ACE=∠CAF=30°,
∴∠BAC=∠BAF-∠CAF=60°-30°=30°.
又∵∠ABC=∠DBF-∠DBA=90°-60°=30°=∠BAC,
∴BC=AC=12海里,
∴(海里),
,
故渔船继续向正东方向行驶,没有触礁的危险.
出示课件13~14,学生独立解决,一生板演,教师订正.
知识点2 坡度、坡角有关的问题
解直角三角形有广泛的应用,解决问题时,要根据实际情况灵活运用相关知识,例如,当我们要测量如图所示大坝或山的高度h时,我们无法直接测量,我们又该如何呢?(出示课件15)
教师问:如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?如何用数量来刻画哪条路陡呢?(出示课件16)
学生思考后,师生共同总结:(出示课件17)
坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示,如图,坡度通常写成的形式.
教师强调:坡度越大,坡角越大,坡面越陡.
出示课件18,学生独立解决并口答,教师订正.
考点1 利用坡度、坡角解答大坝问题
例 如图,防洪大堤的横截面是梯形 ABCD,其中AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)(出示课件19)
学生独立思考后,师生共同解答:(出示课件20)
解:过点A作AF⊥BC于点F,
在Rt△ABF中,∠ABF=∠α=60°,
则AF=AB·sin60°=(m),
在Rt△AEF中,∠E=∠β=45°,则(m).
故改造后的坡长AE为m.
出示课件21~22,学生独立解决,一生板演,教师订正.
考点2 利用坡度、坡角解答山坡问题
例 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,沿山坡向上走了240m到达点C.这座山坡的坡角是多少度?小刚上升了多少米(角度精确到0.01°,长度精确到0.1m)?(出示课件23)
学生独立思考后,师生共同解答:(出示课件24)
解:用α表示坡角的大小,由题意可得
因此α≈26.57°.
在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,
因此
从而BC=240×sin26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3m.
出示课件25,学生独立解决,教师订正.
(三)课堂练习(出示课件26-36)
练习课件26-36页题目,巩固所学知识点,约用时20分钟。
(四)课堂小结(出示课件21)
本节课你有哪些收获?你还有什么困惑吗?(引导学生思考答复)
师生一起提炼本节课的重要知识和必须掌握的技能:
1.方向角的定义:指北或指南方向线与目标方向线所成的小于90°的角.
2.坡角:坡面与水平面的夹角叫做坡角,用字母α表示.
3.坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母i表示.
4.坡度越大,坡角越大,坡面越陡.
(五)课前预习
预习下节课(29.1(第1课时))的相关内容.
知道什么是投影、平行投影及中心投影.
课后作业
教材第77页练习第2题.
板书设计
28.2.2 应用举例(第3课时)
1.方向角的意义;
2.坡度、坡角的意义;
3.例题
九、教学反思
将解直角三角形应用到实际生活中,有利于培养学生的空间想象能力,即要求学生通过对实物的观察或根据文字语言中的某些条件,画出适合他们的图形.这一方面在教学过程应由学生展开,并留给学生思考的时间,给学生充分的自主思考空间和时间,让学生积极主动地学习.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
