物理人教版(2019)必修第二册6.3向心加速度(共27张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册6.3向心加速度(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 55.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-16 23:53:50 | ||
图片预览








文档简介
(共27张PPT)
第六章
人教版 高中物理必修二
第3节 向心加速度
加速度的大小
02
加速度的方向
01
拓展学习
03
总结提升
04
梦天实验舱在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
课堂引入
匀速圆周运动的加速度方向
PART 01
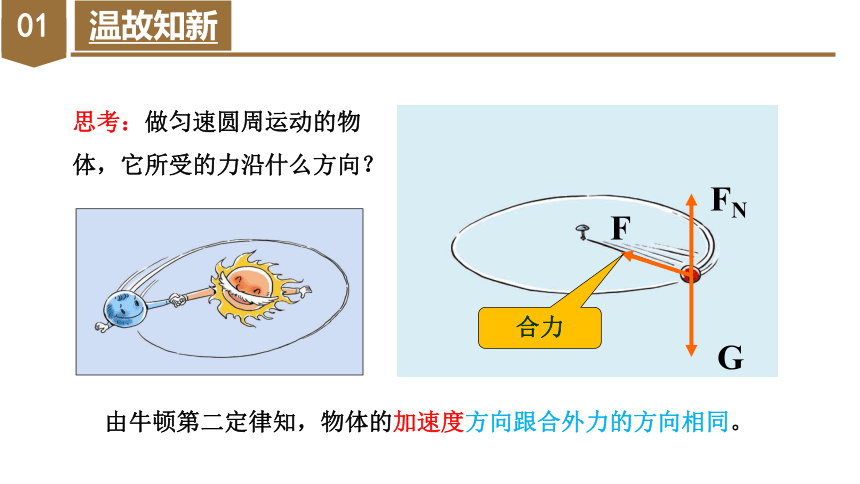
思考:做匀速圆周运动的物体,它所受的力沿什么方向?
G
FN
F
合力
由牛顿第二定律知,物体的加速度方向跟合外力的方向相同。
温故知新
01
1.向心加速度:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度。
4.物理意义:描述速度方向变化的快慢
2.符号:an
3.方向:始终指向圆心
5.说明:匀速圆周运动加速度的方向时刻改变,所以匀速圆周运动不是匀变速运动,而是变加速运动。
向心加速度
02
如何求大小呢?
v
a
Fn
匀速圆周运动的加速度大小
PART 02
如图,物体做匀速圆周运动,经Δt从A运动到B,画出Δv的方向
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δt趋于0时,Δv 逐渐趋向于平行 OA,即Δv指向圆心,此时加速度a也指向圆心。
O
A
B
vA
vB
Δv
Δv
学以致用
01
1.产生:由向心力产生
3.说明:匀速圆周运动的向心加速度大小不变。
2.大小:根据牛顿第二定律和向心力表达式 ,可得出向心加速度的大小
向心加速度的大小
02
对于向心加速度的公式,同学们有各自的看法。从 看,向心加速度与半径成反比;从a=ω2r看,向心加速度与半径成正比。这两个结论是否矛盾?谈谈你的看法。
当v一定时,a与r成反比
当ω一定时,a与r成正比
思考与讨论
03
【例题】如图 所示,在长为 l 的细绳下端拴一个质量为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应该增大小球运动的角速度 ω。
教材例题
04
Fn
m
O
r
F
l
G
【分析】 由于小球在水平面内做圆周运动,向心加速度的方向始终指向圆心。可以根据受力分析,求出向心力的大小,进而求出向心加速度的大小。根据向心加速度公式,分析小球做圆周运动的角速度 ω 与夹角 θ 之间的关系。
Fn
m
O
r
F
l
G
教材例题
04
【解析】 根据对小球的受力分析,可得向心力:Fn = mgtanθ
根据牛顿第二定律可得小球运动的向心加速度
an = Fn/m = gtan θ (1)
根据几何关系可知小球做圆周运动的半径 r=lsin θ (2)
把向心加速度公式 an=ω2r 和(2)式代入(1)式,可得 cosθ =—
g
lω2
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
教材例题
04
拓展学习
PART 03
我们从加速度的定义a= △ v/△t的角度讨论向心加速度的大小
一、速度的变化量
甲
v1
△v
v2
(1)若v1 < v2
1.直线运动的物体:如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v △v是矢量还是标量?
乙
v1
△v
v2
(2)若v1 > v2
速度的变化量
01
2.曲线运动的物体:如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v
v1
△v
v2
设质点初速度为v1,末速度为v2,则速度的变化量Δv = v2 - v1,
移项得: v1+ Δv = v2
v1
v2
Δv
结论: 速度的变化量Δv可以用初速度v1末端指向末速度v2末端的有向线段来表示。
速度的变化量
01
物体从A点经时间Δt沿圆周匀速率运动到B点,转过的角度为Δθ,如图所示,因为vA与OA垂直,vB与OB垂直,且vA=vB,OA=OB,所以△OAB与vA、vB、Δv组成的矢量三角形相似.
向心加速度的推导
02
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
向心加速度的推导
02
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
向心加速度的推导
02
总结提升
PART 04
课堂小结
大小
方向
拓展
向心加速度:匀速圆周运动的加速度
意义:描述速度方向变化的快慢
方向:始终指向圆心(时刻改变)
当v一定时,a与r成反比
当ω一定时,a与r成正比
匀速圆周运动的加速度公式推导
【练习1】(2022春·广东惠州·高一惠州一中)(多选)物体做圆周运动,关于向心加速度,以下说法中正确的是( )
A.向心加速度只改变线速度的方向
B.向心加速度的方向一直指向圆心,所以方向不变
C.由 可知,当线速度保持不变时,向心加速度与半径成反比
D.向心加速度越大,则速度方向改变越大
【参考答案】AC
课堂练习
【练习2】(多选)某高中开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕上每隔4 s均匀“点”一次奶油, 蛋糕一周均匀“点”上15个奶油,则下列说法正确的是( )
A.圆盘转动的转速约为2 πr/min
B.圆盘转动的角速度大小为
C.蛋糕边缘的奶油线速度大小约为
D.蛋糕边缘的奶油向心加速度约为
【参考答案】BD
课堂练习
【练习3】(多选)如图所示,地球绕与赤道面垂直的地轴由西向东匀速转动,O为地心。A点和C点位于赤道上,B点与C点位于同一条经线上。以地心O为参考系,记A、B、C三点的线速度大小分别为vA、vB和vC,向心加速度大小分别为aA、aB和aC,绕地轴转动的周期分别为TA、TB和TC,下列说法正确的是( )
A.vA=vC>vB
B.TA=TB>TC
C.aA=aC>aB
D.aA、aB和aC的方向均始终指向地心O
【参考答案】AC
课堂练习
【练习4】(2022春·山东临沂·高一)荡秋千是人们平时喜爱的一项休闲娱乐活动,如图所示,某同学正在荡秋千,A和B分别为运动过程中的最低点和最高点,若忽略空气阻力,则下列说法正确的是( )
A.在B位置时,该同学速度为零,处于平衡状态
B.在A位置时,该秋千踏板对同学的支持力大于该同学对秋千踏板的压力
C.由B到A过程中,该同学受到的合外力提供向心力
D.由B到A过程中,该同学向心加速度逐渐增大
【参考答案】D
课堂练习
【练习5】如图所示,科技馆中的科普器材中常有齿轮传动装置,已知三个齿轮的半径之比RA:RB:RC=3∶1∶2,当齿轮转动的时候,下列说法中正确的是( )
A.三个齿轮的角速度大小之比ωA:ωB:ωC为1∶1∶1
B.三个齿轮的周期大小之比TA:TB:TC为2∶1∶3
C.三个齿轮边缘的线速度大小之比vA:vB:vC为3∶1∶2
D.三个齿轮边缘的的向心加速度大小之比aA:aB:aC为2∶6∶3
【参考答案】D
课堂练习
【练习6】(2022春·广东肇庆)甲同学在周五离校时,看到乙同学的家长用某型号汽车接其回家,甲同学观察该汽车的后雨刮器,如图所示。设雨刮器摆臂可视为绕O点旋转的折杆OAB,如图所示,OA长度a、AB长度3a, ,AB部分装有胶条,雨刮器工作时胶条紧贴后窗平面可视为匀速率转动。雨刮器工作时下列说法正确的是( )
A.A、B两点线速度大小之比为1∶4
B.A、B角速度之比1∶3
C.A、B加速度大小之比为1∶
D.B点加速度方向沿着AB指向A
【参考答案】C
课堂练习
第六章
人教版 高中物理必修二
第3节 向心加速度
加速度的大小
02
加速度的方向
01
拓展学习
03
总结提升
04
梦天实验舱在轨飞行时,可认为它绕地球做匀速圆周运动。尽管线速度大小不变,但方向却时刻变化,因此,它运动的加速度一定不为 0。那么,该如何确定它在轨飞行时加速度的方向和大小呢?
课堂引入
匀速圆周运动的加速度方向
PART 01
思考:做匀速圆周运动的物体,它所受的力沿什么方向?
G
FN
F
合力
由牛顿第二定律知,物体的加速度方向跟合外力的方向相同。
温故知新
01
1.向心加速度:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度。
4.物理意义:描述速度方向变化的快慢
2.符号:an
3.方向:始终指向圆心
5.说明:匀速圆周运动加速度的方向时刻改变,所以匀速圆周运动不是匀变速运动,而是变加速运动。
向心加速度
02
如何求大小呢?
v
a
Fn
匀速圆周运动的加速度大小
PART 02
如图,物体做匀速圆周运动,经Δt从A运动到B,画出Δv的方向
Δv
O
A
B
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
Δt趋于0时,Δv 逐渐趋向于平行 OA,即Δv指向圆心,此时加速度a也指向圆心。
O
A
B
vA
vB
Δv
Δv
学以致用
01
1.产生:由向心力产生
3.说明:匀速圆周运动的向心加速度大小不变。
2.大小:根据牛顿第二定律和向心力表达式 ,可得出向心加速度的大小
向心加速度的大小
02
对于向心加速度的公式,同学们有各自的看法。从 看,向心加速度与半径成反比;从a=ω2r看,向心加速度与半径成正比。这两个结论是否矛盾?谈谈你的看法。
当v一定时,a与r成反比
当ω一定时,a与r成正比
思考与讨论
03
【例题】如图 所示,在长为 l 的细绳下端拴一个质量为 m 的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为 θ 时,小球运动的向心加速度 an 的大小为多少?通过计算说明 :要增大夹角 θ,应该增大小球运动的角速度 ω。
教材例题
04
Fn
m
O
r
F
l
G
【分析】 由于小球在水平面内做圆周运动,向心加速度的方向始终指向圆心。可以根据受力分析,求出向心力的大小,进而求出向心加速度的大小。根据向心加速度公式,分析小球做圆周运动的角速度 ω 与夹角 θ 之间的关系。
Fn
m
O
r
F
l
G
教材例题
04
【解析】 根据对小球的受力分析,可得向心力:Fn = mgtanθ
根据牛顿第二定律可得小球运动的向心加速度
an = Fn/m = gtan θ (1)
根据几何关系可知小球做圆周运动的半径 r=lsin θ (2)
把向心加速度公式 an=ω2r 和(2)式代入(1)式,可得 cosθ =—
g
lω2
从此式可以看出,当小球运动的角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
教材例题
04
拓展学习
PART 03
我们从加速度的定义a= △ v/△t的角度讨论向心加速度的大小
一、速度的变化量
甲
v1
△v
v2
(1)若v1 < v2
1.直线运动的物体:如果初速度v1和末速度v2在同一方向上,如何表示速度的变化量△v △v是矢量还是标量?
乙
v1
△v
v2
(2)若v1 > v2
速度的变化量
01
2.曲线运动的物体:如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v
v1
△v
v2
设质点初速度为v1,末速度为v2,则速度的变化量Δv = v2 - v1,
移项得: v1+ Δv = v2
v1
v2
Δv
结论: 速度的变化量Δv可以用初速度v1末端指向末速度v2末端的有向线段来表示。
速度的变化量
01
物体从A点经时间Δt沿圆周匀速率运动到B点,转过的角度为Δθ,如图所示,因为vA与OA垂直,vB与OB垂直,且vA=vB,OA=OB,所以△OAB与vA、vB、Δv组成的矢量三角形相似.
向心加速度的推导
02
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
向心加速度的推导
02
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
向心加速度的推导
02
总结提升
PART 04
课堂小结
大小
方向
拓展
向心加速度:匀速圆周运动的加速度
意义:描述速度方向变化的快慢
方向:始终指向圆心(时刻改变)
当v一定时,a与r成反比
当ω一定时,a与r成正比
匀速圆周运动的加速度公式推导
【练习1】(2022春·广东惠州·高一惠州一中)(多选)物体做圆周运动,关于向心加速度,以下说法中正确的是( )
A.向心加速度只改变线速度的方向
B.向心加速度的方向一直指向圆心,所以方向不变
C.由 可知,当线速度保持不变时,向心加速度与半径成反比
D.向心加速度越大,则速度方向改变越大
【参考答案】AC
课堂练习
【练习2】(多选)某高中开设了糕点制作的选修课,小明同学在体验糕点制作“裱花”环节时,他在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕上每隔4 s均匀“点”一次奶油, 蛋糕一周均匀“点”上15个奶油,则下列说法正确的是( )
A.圆盘转动的转速约为2 πr/min
B.圆盘转动的角速度大小为
C.蛋糕边缘的奶油线速度大小约为
D.蛋糕边缘的奶油向心加速度约为
【参考答案】BD
课堂练习
【练习3】(多选)如图所示,地球绕与赤道面垂直的地轴由西向东匀速转动,O为地心。A点和C点位于赤道上,B点与C点位于同一条经线上。以地心O为参考系,记A、B、C三点的线速度大小分别为vA、vB和vC,向心加速度大小分别为aA、aB和aC,绕地轴转动的周期分别为TA、TB和TC,下列说法正确的是( )
A.vA=vC>vB
B.TA=TB>TC
C.aA=aC>aB
D.aA、aB和aC的方向均始终指向地心O
【参考答案】AC
课堂练习
【练习4】(2022春·山东临沂·高一)荡秋千是人们平时喜爱的一项休闲娱乐活动,如图所示,某同学正在荡秋千,A和B分别为运动过程中的最低点和最高点,若忽略空气阻力,则下列说法正确的是( )
A.在B位置时,该同学速度为零,处于平衡状态
B.在A位置时,该秋千踏板对同学的支持力大于该同学对秋千踏板的压力
C.由B到A过程中,该同学受到的合外力提供向心力
D.由B到A过程中,该同学向心加速度逐渐增大
【参考答案】D
课堂练习
【练习5】如图所示,科技馆中的科普器材中常有齿轮传动装置,已知三个齿轮的半径之比RA:RB:RC=3∶1∶2,当齿轮转动的时候,下列说法中正确的是( )
A.三个齿轮的角速度大小之比ωA:ωB:ωC为1∶1∶1
B.三个齿轮的周期大小之比TA:TB:TC为2∶1∶3
C.三个齿轮边缘的线速度大小之比vA:vB:vC为3∶1∶2
D.三个齿轮边缘的的向心加速度大小之比aA:aB:aC为2∶6∶3
【参考答案】D
课堂练习
【练习6】(2022春·广东肇庆)甲同学在周五离校时,看到乙同学的家长用某型号汽车接其回家,甲同学观察该汽车的后雨刮器,如图所示。设雨刮器摆臂可视为绕O点旋转的折杆OAB,如图所示,OA长度a、AB长度3a, ,AB部分装有胶条,雨刮器工作时胶条紧贴后窗平面可视为匀速率转动。雨刮器工作时下列说法正确的是( )
A.A、B两点线速度大小之比为1∶4
B.A、B角速度之比1∶3
C.A、B加速度大小之比为1∶
D.B点加速度方向沿着AB指向A
【参考答案】C
课堂练习
