鲁教版六年级数学下册6.2.2积的乘方 课件(共23张PPT)
文档属性
| 名称 | 鲁教版六年级数学下册6.2.2积的乘方 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 277.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 08:35:59 | ||
图片预览




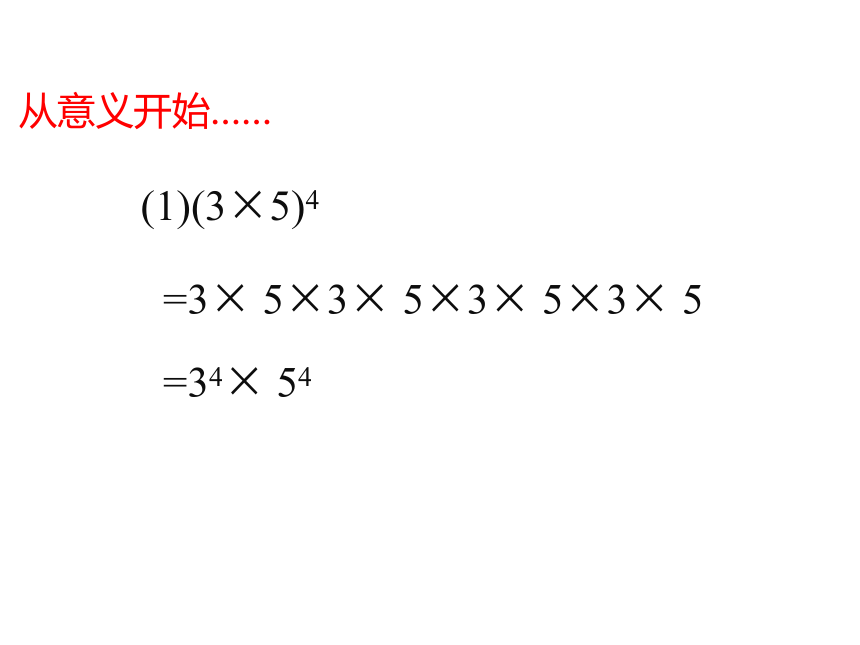




文档简介
(共23张PPT)
6.2.2积的乘方
初中一年级数学
回顾&思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m,n都是正整数)
amn
地球可以近似地看做是球体,地球的半径约为6×103km,它的体积大约是多少立方千米?
那么(6×103)3等于多少?
积乘方
从简单开始……
(1)(3×5)4
(2)(3×5)m
(3)(ab)n
从意义开始……
(1)(3×5)4
=3× 5×3× 5×3× 5×3× 5
=34× 54
从意义开始……
(2)(3×5)m
=3× 5×……×3× 5(m个3×5相乘 )
=3m× 5m
从意义开始……
(3)(ab)n
=ab× ab×……×ab(n个ab相乘 )
=an bn
积的乘方等于 .
(ab)n =
an·bn
积乘方
乘方的积
(m,n都是正整数)
把积的每个因式分别乘方,再把所得的幂相乘.
积的乘方法则
(a+b)n可以用积的乘方法则计算吗
即 (a+b)n= an·bn 成立吗?
又 (a+b)n= an+bn 成立吗?
积的乘方法则
例题解析
例2 计算:
(1) (3x)2 ; (2) (-2b)5 ;
(3) (-2xy)4 ; (4) (3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5 ;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n
=16x4 y4 ;
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
(1)(ab4)4=ab8 ( )
×
(2) (3xy)3=9x3y3 ( )
(3) (-3pq)2=-6 p2q2 ( )
(4) -(-ab2)2=a2b4 ( )
×
×
×
下面的计算是否准确?如果有错误请改正
结果应为a4b16
结果应为27x3y3
结果应为9p2q2
结果应为-a2b4
例3 计算:x3 · x5+(x2)4+(-2 x4)2
解:
x3 · x5+(x2)4+(-2 x4)2
= x8+ x8+4x8
=6x8
方法总结:涉及积的乘方的混合运算,一般先算积的乘方,再算乘法,最后算加减,合并同类项.
1、计算:
(–3n)3 ;
(5xy)3 ;
(3b)2
–(ab)2
(–4a2)3
(y2z3)3
(xy4)m
–(p2q)n
随堂训练
解:
(–3n)3 =(–3)3n3= –27n3;
(5xy)3=53x3y3=125x3y3;
(3b)2=32b2=9b2;
–(ab)2= –a2b2;
(–4a2)3=(–4)3(a2)3= –64a6;
(y2z3)3=(y2)3(z3)3=y6z9;
(xy4)m=xm(y4)m=xmy4m;
–(p2q)n= –(p2)nqn= –p2nqn;
2、计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-3ab2c3)3; (4)(-xmy3m)2.
随堂训练
(4)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
(3)(-3ab2c3)3=(-3)3a3b6c9=-27a3b6c9;
3、计算:
–a3 +(–4a)2 a (2)(xny3n)2 +(x2y6)n
–a3 +(–4a)2 a
= –a3 +16a2 a
= –a3 +16a3
=15a3
解:
(xny3n)2 +(x2y6)n
=x2ny6n +x2ny6n
=2x2ny6n
解:
(3) (–3x3)2 – [(2x)2]3
(–3x3)2 – [(2x)2]3
=9x6 – (2x)6
=9x6 – 64x6
= – 55x6
(4) [(x+y)(x-y)]3
[(x+y)(x-y)]3
=(x+y)3(x-y)3
解:
解:
公 式 的 拓 展
三个或三个以上的积的乘方,是否也具有上面的性质 怎样用公式表示
(abc)n=an·bn·cn
怎样证明
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
公式的逆向应用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
计算:
说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。
解:原式
2.计算:
过手练习
过手练习
过手练习
本节课你的收获是什么?
{
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方= .
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
6.2.2积的乘方
初中一年级数学
回顾&思考
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an
=am+n
(m,n都是正整数)
幂的乘方运算法则:
(am)n= (m,n都是正整数)
amn
地球可以近似地看做是球体,地球的半径约为6×103km,它的体积大约是多少立方千米?
那么(6×103)3等于多少?
积乘方
从简单开始……
(1)(3×5)4
(2)(3×5)m
(3)(ab)n
从意义开始……
(1)(3×5)4
=3× 5×3× 5×3× 5×3× 5
=34× 54
从意义开始……
(2)(3×5)m
=3× 5×……×3× 5(m个3×5相乘 )
=3m× 5m
从意义开始……
(3)(ab)n
=ab× ab×……×ab(n个ab相乘 )
=an bn
积的乘方等于 .
(ab)n =
an·bn
积乘方
乘方的积
(m,n都是正整数)
把积的每个因式分别乘方,再把所得的幂相乘.
积的乘方法则
(a+b)n可以用积的乘方法则计算吗
即 (a+b)n= an·bn 成立吗?
又 (a+b)n= an+bn 成立吗?
积的乘方法则
例题解析
例2 计算:
(1) (3x)2 ; (2) (-2b)5 ;
(3) (-2xy)4 ; (4) (3a2)n .
=32x2
= 9x2 ;
(1) (3x)2
解:
(2) (-2b)5
= (-2)5b5
= -32b5 ;
(3) (-2xy)4
= (-2x)4 y4
= (-2)4 x4 y4
(4) (3a2)n
= 3n (a2)n
= 3n a2n
=16x4 y4 ;
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
(1)(ab4)4=ab8 ( )
×
(2) (3xy)3=9x3y3 ( )
(3) (-3pq)2=-6 p2q2 ( )
(4) -(-ab2)2=a2b4 ( )
×
×
×
下面的计算是否准确?如果有错误请改正
结果应为a4b16
结果应为27x3y3
结果应为9p2q2
结果应为-a2b4
例3 计算:x3 · x5+(x2)4+(-2 x4)2
解:
x3 · x5+(x2)4+(-2 x4)2
= x8+ x8+4x8
=6x8
方法总结:涉及积的乘方的混合运算,一般先算积的乘方,再算乘法,最后算加减,合并同类项.
1、计算:
(–3n)3 ;
(5xy)3 ;
(3b)2
–(ab)2
(–4a2)3
(y2z3)3
(xy4)m
–(p2q)n
随堂训练
解:
(–3n)3 =(–3)3n3= –27n3;
(5xy)3=53x3y3=125x3y3;
(3b)2=32b2=9b2;
–(ab)2= –a2b2;
(–4a2)3=(–4)3(a2)3= –64a6;
(y2z3)3=(y2)3(z3)3=y6z9;
(xy4)m=xm(y4)m=xmy4m;
–(p2q)n= –(p2)nqn= –p2nqn;
2、计算:(1)(-5ab)3; (2)-(3x2y)2;
(3)(-3ab2c3)3; (4)(-xmy3m)2.
随堂训练
(4)(-xmy3m)2=(-1)2x2my6m=x2my6m.
解:(1)(-5ab)3=(-5)3a3b3=-125a3b3;
(2)-(3x2y)2=-32x4y2=-9x4y2;
(3)(-3ab2c3)3=(-3)3a3b6c9=-27a3b6c9;
3、计算:
–a3 +(–4a)2 a (2)(xny3n)2 +(x2y6)n
–a3 +(–4a)2 a
= –a3 +16a2 a
= –a3 +16a3
=15a3
解:
(xny3n)2 +(x2y6)n
=x2ny6n +x2ny6n
=2x2ny6n
解:
(3) (–3x3)2 – [(2x)2]3
(–3x3)2 – [(2x)2]3
=9x6 – (2x)6
=9x6 – 64x6
= – 55x6
(4) [(x+y)(x-y)]3
[(x+y)(x-y)]3
=(x+y)3(x-y)3
解:
解:
公 式 的 拓 展
三个或三个以上的积的乘方,是否也具有上面的性质 怎样用公式表示
(abc)n=an·bn·cn
怎样证明
(abc)n=[(ab)·c]n
=(ab)n·cn
= an·bn·cn.
公式的逆向应用
(ab)n = an·bn
(m,n都是正整数)
反向使用:
an·bn = (ab)n
计算:
说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。
解:原式
2.计算:
过手练习
过手练习
过手练习
本节课你的收获是什么?
{
幂的意义:
a·a· … ·a
n个a
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方= .
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
