数学人教A版(2019)必修第二册6.4.2向量在物理中的应用(共18张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册6.4.2向量在物理中的应用(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 427.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 11:33:10 | ||
图片预览





文档简介
(共18张PPT)
向量在物理中的应用
新知探究
问题1 向量加法的平行四边形法则、三角形法则、数量积的物理模型分别是什么?
向量加法的平行四边形的物理模型是力(速度)的合成与分解;
向量的数量积的物理模型是力对物体所做的功.
向量加法的三角形法则的物理模型是位移的合成;
新知探究
问题2 向量的运算与速度、加速度与位移有什么联系?
速度、加速度与位移的合成与分解,实质上是向量的加减法运算,
而运动的叠加也用到向量的合成.
新知探究
问题3 向量的数量积与功有什么联系?
物理上力做功的实质是力在物体前进方向上的分力与物体位移的乘积,
它的实质是向量的数量积.
新知探究
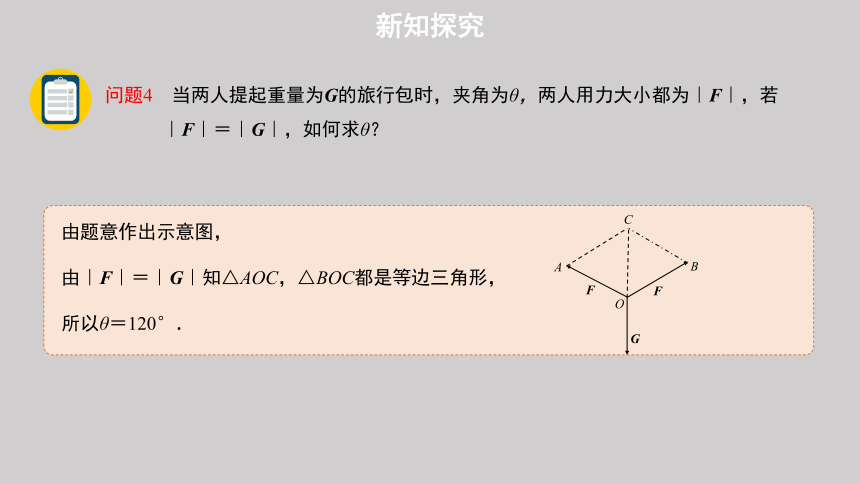
问题4 当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若
|F|=|G|,如何求θ?
由题意作出示意图,
所以θ=120°.
由|F|=|G|知△AOC,△BOC都是等边三角形,
新知探究
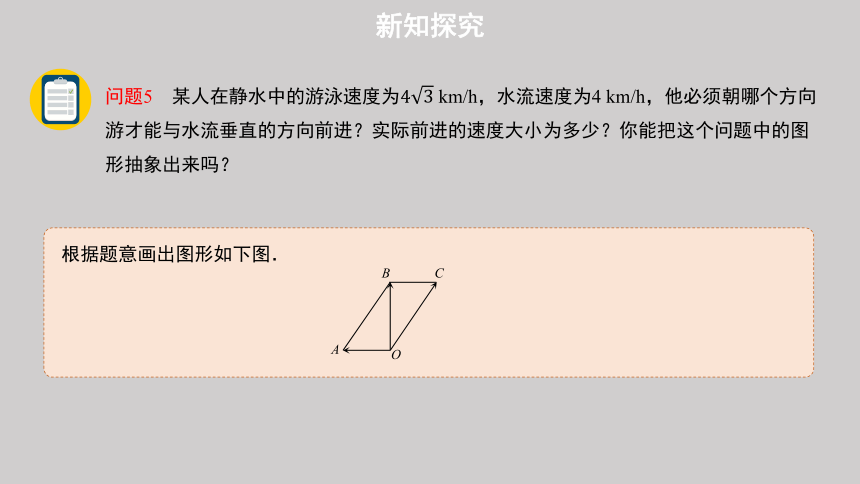
问题5 某人在静水中的游泳速度为 km/h,水流速度为4 km/h,他必须朝哪个方向游才能与水流垂直的方向前进?实际前进的速度大小为多少?你能把这个问题中的图形抽象出来吗?
根据题意画出图形如下图.
A
O
B
C
初步应用
例1 如图所示,用两条成120°角的等长的绳子悬挂一个灯具,已知灯具重10 N,那么每根绳子的拉力大小分别是多少?
解答:如图,设灯具的重力为G,每根绳的拉力分别为,
则由题意得与都成60°角,
且||cos 60°+||cos 60°=| G |=10,
即每根绳子的拉力大小都为10 N.
120°
G
F1
F2
||=||=10,
初步应用
例2 如图所示,已知力F与水平方向的夹角为30°(斜向上),大小为50 N,一个质量为8 kg的木块受力的作用在动摩擦因数μ=0.02的水平平面上运动了20 m.求力F和摩擦力f所做的功.(g=10 N/kg)
解答:设木块的位移为s,
如图,将力F分解,
它在竖直方向上的分力的大小为:
设木块的重力为G,摩擦力f的大小为:
sin 30°=25(N).
=1.1(N),
因此,做功为:
30°
f
F
F1
F2
则力F做功为:
F cos 30°=(J).
cos 180°=-22(J).
G
初步应用
例3 如图所示,已知质点由点A(20,15)移动到点B(7,0)的过程中,两恒力F1=(3,4),F2=(6,-5)作用于该质点.
x
y
A
B
O
F1
F2
20
15
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
如何求例3中力所做的功?
力F1,F2所做的功,分别为F1 , F2 ,
合力F所做功为F .
然后再根据数量积的坐标运算求解.
课堂练习
练习:教科书第122页练习1,2.
归纳小结
(1)利用向量法解决物理问题思路是什么?
(2)向量方法解决物理问题的步骤是什么?
问题6 本节课收获了哪些知识,请你从以下几方面总结:
(1)用向量理论讨论物理学中的相关问题,一般来说分为四个步骤:
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
(3)你有什么困惑吗?
④回答问题,即把所得的数学结论回归到物理问题.
归纳小结
(1)利用向量法解决物理问题思路是什么?
(2)向量方法解决物理问题的步骤是什么?
问题6 本节课收获了哪些知识,请你从以下几方面总结:
(2)利用向量法解决物理问题有两种思路,
第一种是几何法,选取适当的基底,将题中涉及的向量用基底表示,
运算律或性质计算.
第二种是坐标法,通过建立平面直角坐标系,实现向量的坐标化,转化为代数运算.
(3)你有什么困惑吗?
(3)困惑是:……
再利用向量运算法则、
作业布置
作业:教科书第123页,练习第3,4,5题,第124页A组12;B组第6题.
已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
1
目标检测
A
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
解析:(3,1)=(8,0),设F的终点坐标为
B∴终点坐标为(9,1),故选A.
2
目标检测
A
A.13 m/s
C.17 m/s
B.12 m/s
D.15 m/s
河水的流速为5 m/s,若一艘小船沿垂直于河岸方向以12 m/s的速度驶向对岸,则小船在静水中的速度大小为( )
解析:设小船在静水中的速度为v1,河水的流速为v2,v1与v2的合速度为v.
∵为了使航向垂直河岸,船头必须斜向上游方向,即小船在静水中的速度v1斜向上游方向,
河水速度v2平行于河岸,合速度v指向对岸,
∴静水速度|v1|==13(m/s).
3
目标检测
3
一条河宽为800 m,一船从A处出发垂直到达河正对岸的B处,船速为20 km/h,水速为12 km/h,则船到达B处所需时间为________ min.
解析:∵v实际=v船+v水=v1+v2,
∴|v实际|=
∴该船到达B处所需的时间为3 min.
|v1|=20 km/h,|v2|=12 km/h,
==16(km/h).
∴所需时间t= =0.05(h)
=3(min).
B
A
水流方向
v实际
v1
v2
4
目标检测
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
解答:(1)=(7,0)-(20,15)=(-13,-15),
W1=F1·=(3,4)·(-13,-15)
W2=F2·=(6,-5)·(-13,-15)
∴力F1,F2对质点所做的功分别为-99和-3.
=3×(-13)+4×(-15)=-99,
=6×(-13)+(-5)×(-15)=-3.
4
目标检测
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
(2)W=F·=(F1+F2)·
=(9,-1)·(-13,-15)
=-117+15=-102.
∴合力F对质点所做的功为-102.
=9×(-13)+(-1)×(-15)
=[(3,4)+(6,-5)]·(-13,-15)
向量在物理中的应用
新知探究
问题1 向量加法的平行四边形法则、三角形法则、数量积的物理模型分别是什么?
向量加法的平行四边形的物理模型是力(速度)的合成与分解;
向量的数量积的物理模型是力对物体所做的功.
向量加法的三角形法则的物理模型是位移的合成;
新知探究
问题2 向量的运算与速度、加速度与位移有什么联系?
速度、加速度与位移的合成与分解,实质上是向量的加减法运算,
而运动的叠加也用到向量的合成.
新知探究
问题3 向量的数量积与功有什么联系?
物理上力做功的实质是力在物体前进方向上的分力与物体位移的乘积,
它的实质是向量的数量积.
新知探究
问题4 当两人提起重量为G的旅行包时,夹角为θ,两人用力大小都为|F|,若
|F|=|G|,如何求θ?
由题意作出示意图,
所以θ=120°.
由|F|=|G|知△AOC,△BOC都是等边三角形,
新知探究
问题5 某人在静水中的游泳速度为 km/h,水流速度为4 km/h,他必须朝哪个方向游才能与水流垂直的方向前进?实际前进的速度大小为多少?你能把这个问题中的图形抽象出来吗?
根据题意画出图形如下图.
A
O
B
C
初步应用
例1 如图所示,用两条成120°角的等长的绳子悬挂一个灯具,已知灯具重10 N,那么每根绳子的拉力大小分别是多少?
解答:如图,设灯具的重力为G,每根绳的拉力分别为,
则由题意得与都成60°角,
且||cos 60°+||cos 60°=| G |=10,
即每根绳子的拉力大小都为10 N.
120°
G
F1
F2
||=||=10,
初步应用
例2 如图所示,已知力F与水平方向的夹角为30°(斜向上),大小为50 N,一个质量为8 kg的木块受力的作用在动摩擦因数μ=0.02的水平平面上运动了20 m.求力F和摩擦力f所做的功.(g=10 N/kg)
解答:设木块的位移为s,
如图,将力F分解,
它在竖直方向上的分力的大小为:
设木块的重力为G,摩擦力f的大小为:
sin 30°=25(N).
=1.1(N),
因此,做功为:
30°
f
F
F1
F2
则力F做功为:
F cos 30°=(J).
cos 180°=-22(J).
G
初步应用
例3 如图所示,已知质点由点A(20,15)移动到点B(7,0)的过程中,两恒力F1=(3,4),F2=(6,-5)作用于该质点.
x
y
A
B
O
F1
F2
20
15
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
如何求例3中力所做的功?
力F1,F2所做的功,分别为F1 , F2 ,
合力F所做功为F .
然后再根据数量积的坐标运算求解.
课堂练习
练习:教科书第122页练习1,2.
归纳小结
(1)利用向量法解决物理问题思路是什么?
(2)向量方法解决物理问题的步骤是什么?
问题6 本节课收获了哪些知识,请你从以下几方面总结:
(1)用向量理论讨论物理学中的相关问题,一般来说分为四个步骤:
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
(3)你有什么困惑吗?
④回答问题,即把所得的数学结论回归到物理问题.
归纳小结
(1)利用向量法解决物理问题思路是什么?
(2)向量方法解决物理问题的步骤是什么?
问题6 本节课收获了哪些知识,请你从以下几方面总结:
(2)利用向量法解决物理问题有两种思路,
第一种是几何法,选取适当的基底,将题中涉及的向量用基底表示,
运算律或性质计算.
第二种是坐标法,通过建立平面直角坐标系,实现向量的坐标化,转化为代数运算.
(3)你有什么困惑吗?
(3)困惑是:……
再利用向量运算法则、
作业布置
作业:教科书第123页,练习第3,4,5题,第124页A组12;B组第6题.
已知作用在点A的三个力F1=(3,4),F2=(2,-5),F3=(3,1)且A(1,1),则合力F=F1+F2+F3的终点坐标为( )
1
目标检测
A
A.(9,1)
B.(1,9)
C.(9,0)
D.(0,9)
解析:(3,1)=(8,0),设F的终点坐标为
B∴终点坐标为(9,1),故选A.
2
目标检测
A
A.13 m/s
C.17 m/s
B.12 m/s
D.15 m/s
河水的流速为5 m/s,若一艘小船沿垂直于河岸方向以12 m/s的速度驶向对岸,则小船在静水中的速度大小为( )
解析:设小船在静水中的速度为v1,河水的流速为v2,v1与v2的合速度为v.
∵为了使航向垂直河岸,船头必须斜向上游方向,即小船在静水中的速度v1斜向上游方向,
河水速度v2平行于河岸,合速度v指向对岸,
∴静水速度|v1|==13(m/s).
3
目标检测
3
一条河宽为800 m,一船从A处出发垂直到达河正对岸的B处,船速为20 km/h,水速为12 km/h,则船到达B处所需时间为________ min.
解析:∵v实际=v船+v水=v1+v2,
∴|v实际|=
∴该船到达B处所需的时间为3 min.
|v1|=20 km/h,|v2|=12 km/h,
==16(km/h).
∴所需时间t= =0.05(h)
=3(min).
B
A
水流方向
v实际
v1
v2
4
目标检测
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
解答:(1)=(7,0)-(20,15)=(-13,-15),
W1=F1·=(3,4)·(-13,-15)
W2=F2·=(6,-5)·(-13,-15)
∴力F1,F2对质点所做的功分别为-99和-3.
=3×(-13)+4×(-15)=-99,
=6×(-13)+(-5)×(-15)=-3.
4
目标检测
(1)求力F1,F2分别对质点所做的功;
(2)求力F1,F2的合力F对质点所做的功.
已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0).
(2)W=F·=(F1+F2)·
=(9,-1)·(-13,-15)
=-117+15=-102.
∴合力F对质点所做的功为-102.
=9×(-13)+(-1)×(-15)
=[(3,4)+(6,-5)]·(-13,-15)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
