9.4探索三角形相似的条件 第1课时 利用角的关系判定两三角形相似 同步练习(含答案)
文档属性
| 名称 | 9.4探索三角形相似的条件 第1课时 利用角的关系判定两三角形相似 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定两三角形相似
基础闯关
知识点一:相似三角形的定义
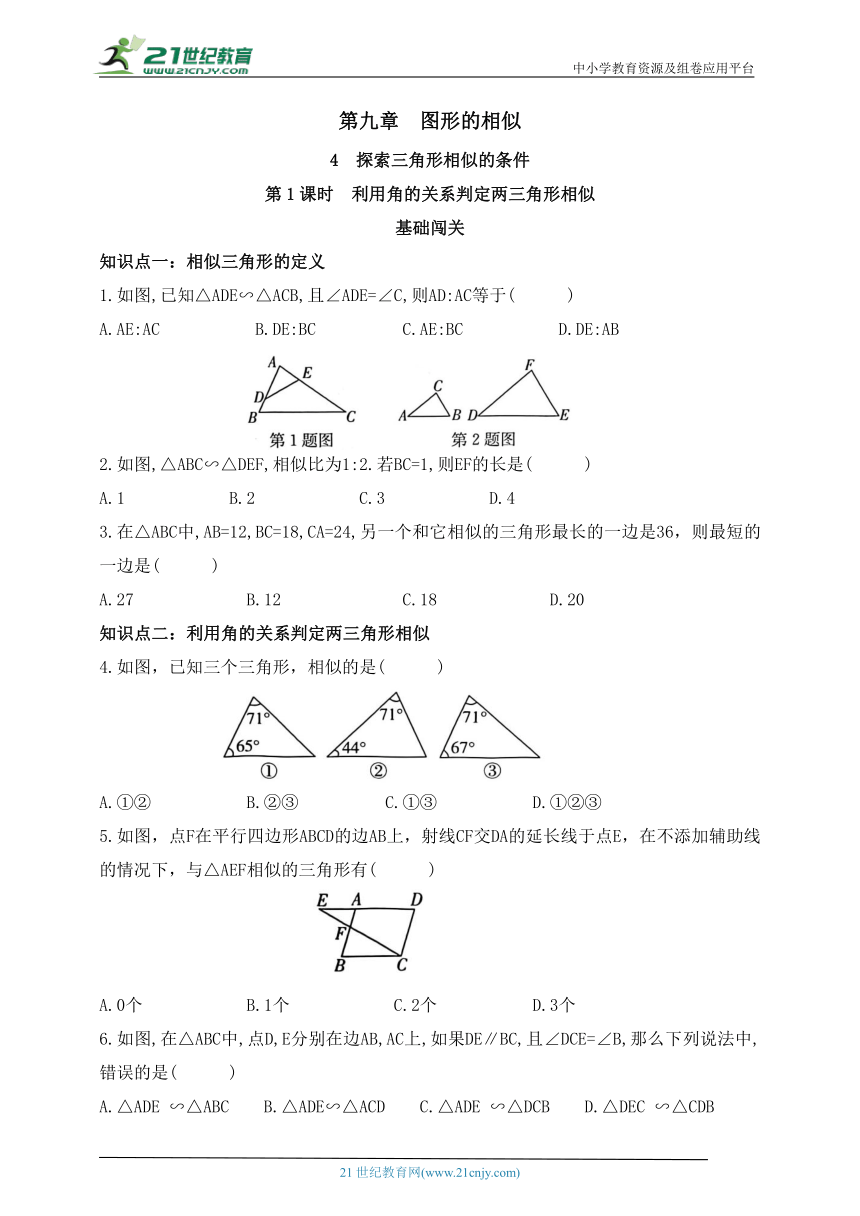
1.如图,已知△ADE∽△ACB,且∠ADE=∠C,则AD:AC等于( )
A.AE:AC B.DE:BC C.AE:BC D.DE:AB
2.如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是( )
A.1 B.2 C.3 D.4
3.在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B.12 C.18 D.20
知识点二:利用角的关系判定两三角形相似
4.如图,已知三个三角形,相似的是( )
A.①② B.②③ C.①③ D.①②③
5.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个
6.如图,在△ABC中,点D,E分别在边AB,AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
A.△ADE ∽△ABC B.△ADE∽△ACD C.△ADE ∽△DCB D.△DEC ∽△CDB
7.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
知识点三:直角三角形相似的判定
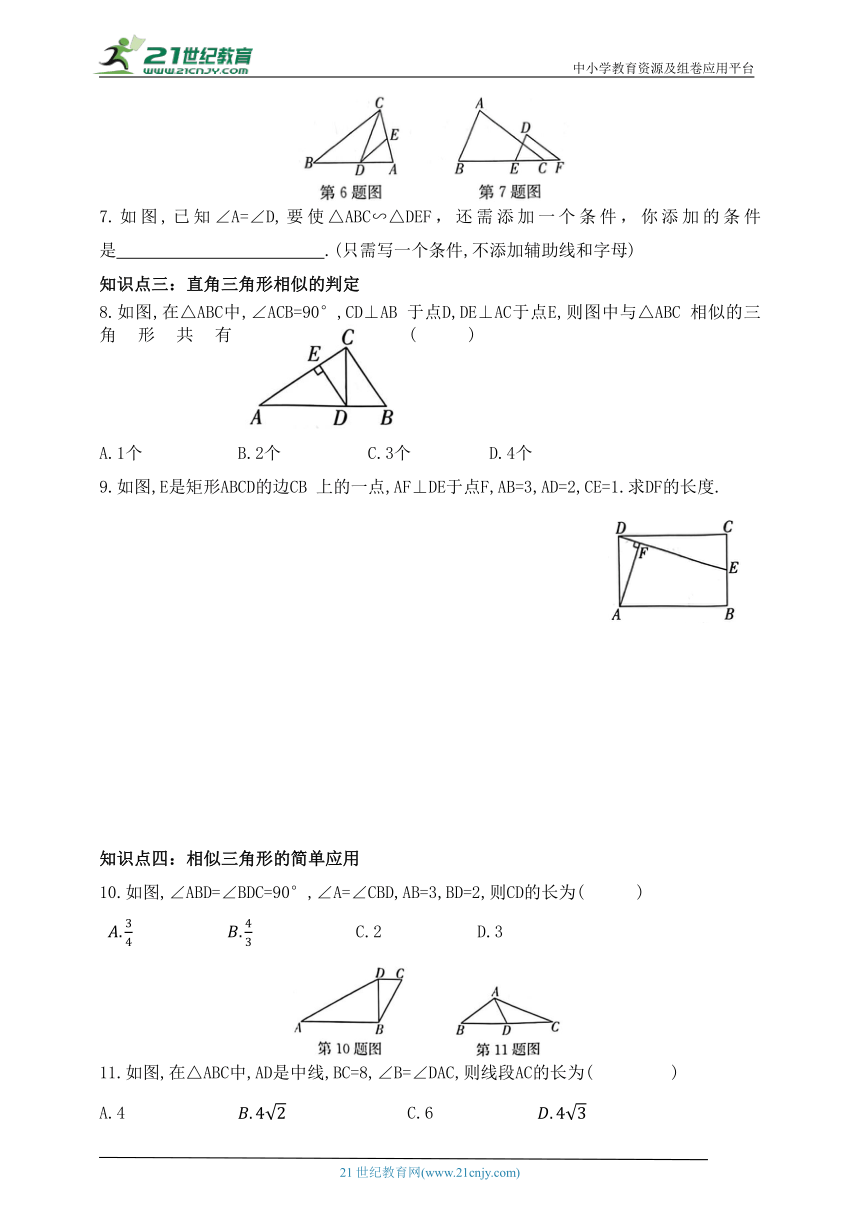
8.如图,在△ABC中,∠ACB=90°,CD⊥AB 于点D,DE⊥AC于点E,则图中与△ABC 相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
9.如图,E是矩形ABCD的边CB 上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
知识点四:相似三角形的简单应用
10.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
C.2 D.3
11.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 C.6
能力提升
12.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A.6 B.8 C.10 D.12
13.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为点F.若DF=6,则线段EF的长为( )
A.2 B.3 C.4 D.5
14.如图,已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:
①分别以A,B为圆心,大于的长为半径画弧,相交于两点M,N;②作直线MN 交射线AP于点D,连接BD;③以B为圆心,BA长为半径画弧,交射线AP于点C.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠CDB=72° B.△ADB ∽△ABC C.CD:AD=2:1 D.∠ABC=3∠ACB
15.[一题多解]如图,矩形ABCD的边长AB=6,BC=8,将矩形折叠,使点B与点D重合,则折痕EF的长 .
培优创新
16.如图,正方形ABCD的顶点A 在等腰直角三角形DEF的斜边EF上,EF 与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF.
(2)求证:△ABG∽△CFG.
参考答案
1.B 2.B 3.C 4.A 5.C 6.C 7.示例:AB∥DE 8.D
9.解:∵四边形ABCD是矩形,∴DC=AB=3,∠ADC=
⊥DE,∴∠AFD=90°=∠C,∠ADF+∠DAF=90°.
又 ∵∠ADF+∠EDC=90°,∴∠EDC=∠DAF,∴△EDC
即
10.B 11.B 12.C 13.B 14.C
16.证明:(1)∵四边形ABCD是正方形,△EDF为等腰直角三角形,
∴∠ADC=∠EDF=90°,DA=DC,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF.
在△DAE和△DCF中, ∴△DAE≌△DCF.
(2)∵△DEF为等腰直角三角形,∴∠E=∠DFE=45°.
∵△DAE≌△DCF,∴∠DFC=∠E=45°,∴∠CFG=∠DFC+∠DFE=90°=∠B.
∵∠AGB=∠CGF,∴△ABG∽△CFG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第1课时 利用角的关系判定两三角形相似
基础闯关
知识点一:相似三角形的定义
1.如图,已知△ADE∽△ACB,且∠ADE=∠C,则AD:AC等于( )
A.AE:AC B.DE:BC C.AE:BC D.DE:AB
2.如图,△ABC∽△DEF,相似比为1:2.若BC=1,则EF的长是( )
A.1 B.2 C.3 D.4
3.在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B.12 C.18 D.20
知识点二:利用角的关系判定两三角形相似
4.如图,已知三个三角形,相似的是( )
A.①② B.②③ C.①③ D.①②③
5.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个
6.如图,在△ABC中,点D,E分别在边AB,AC上,如果DE∥BC,且∠DCE=∠B,那么下列说法中,错误的是( )
A.△ADE ∽△ABC B.△ADE∽△ACD C.△ADE ∽△DCB D.△DEC ∽△CDB
7.如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
知识点三:直角三角形相似的判定
8.如图,在△ABC中,∠ACB=90°,CD⊥AB 于点D,DE⊥AC于点E,则图中与△ABC 相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
9.如图,E是矩形ABCD的边CB 上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
知识点四:相似三角形的简单应用
10.如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
C.2 D.3
11.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 C.6
能力提升
12.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
A.6 B.8 C.10 D.12
13.如图,在矩形ABCD中,AB=3,BC=10,点E在BC边上,DF⊥AE,垂足为点F.若DF=6,则线段EF的长为( )
A.2 B.3 C.4 D.5
14.如图,已知∠PAQ=36°,点B为射线AQ上一固定点,按以下步骤作图:
①分别以A,B为圆心,大于的长为半径画弧,相交于两点M,N;②作直线MN 交射线AP于点D,连接BD;③以B为圆心,BA长为半径画弧,交射线AP于点C.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠CDB=72° B.△ADB ∽△ABC C.CD:AD=2:1 D.∠ABC=3∠ACB
15.[一题多解]如图,矩形ABCD的边长AB=6,BC=8,将矩形折叠,使点B与点D重合,则折痕EF的长 .
培优创新
16.如图,正方形ABCD的顶点A 在等腰直角三角形DEF的斜边EF上,EF 与BC相交于点G,连接CF.
(1)求证:△DAE≌△DCF.
(2)求证:△ABG∽△CFG.
参考答案
1.B 2.B 3.C 4.A 5.C 6.C 7.示例:AB∥DE 8.D
9.解:∵四边形ABCD是矩形,∴DC=AB=3,∠ADC=
⊥DE,∴∠AFD=90°=∠C,∠ADF+∠DAF=90°.
又 ∵∠ADF+∠EDC=90°,∴∠EDC=∠DAF,∴△EDC
即
10.B 11.B 12.C 13.B 14.C
16.证明:(1)∵四边形ABCD是正方形,△EDF为等腰直角三角形,
∴∠ADC=∠EDF=90°,DA=DC,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF.
在△DAE和△DCF中, ∴△DAE≌△DCF.
(2)∵△DEF为等腰直角三角形,∴∠E=∠DFE=45°.
∵△DAE≌△DCF,∴∠DFC=∠E=45°,∴∠CFG=∠DFC+∠DFE=90°=∠B.
∵∠AGB=∠CGF,∴△ABG∽△CFG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
