9.4探索三角形相似的条件 第2课时 利用边角关系判定两三角形相似 同步练习(含答案)
文档属性
| 名称 | 9.4探索三角形相似的条件 第2课时 利用边角关系判定两三角形相似 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:08:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角关系判定两三角形相似
基础闯关
知识点一:利用边角关系判定两三角形相似
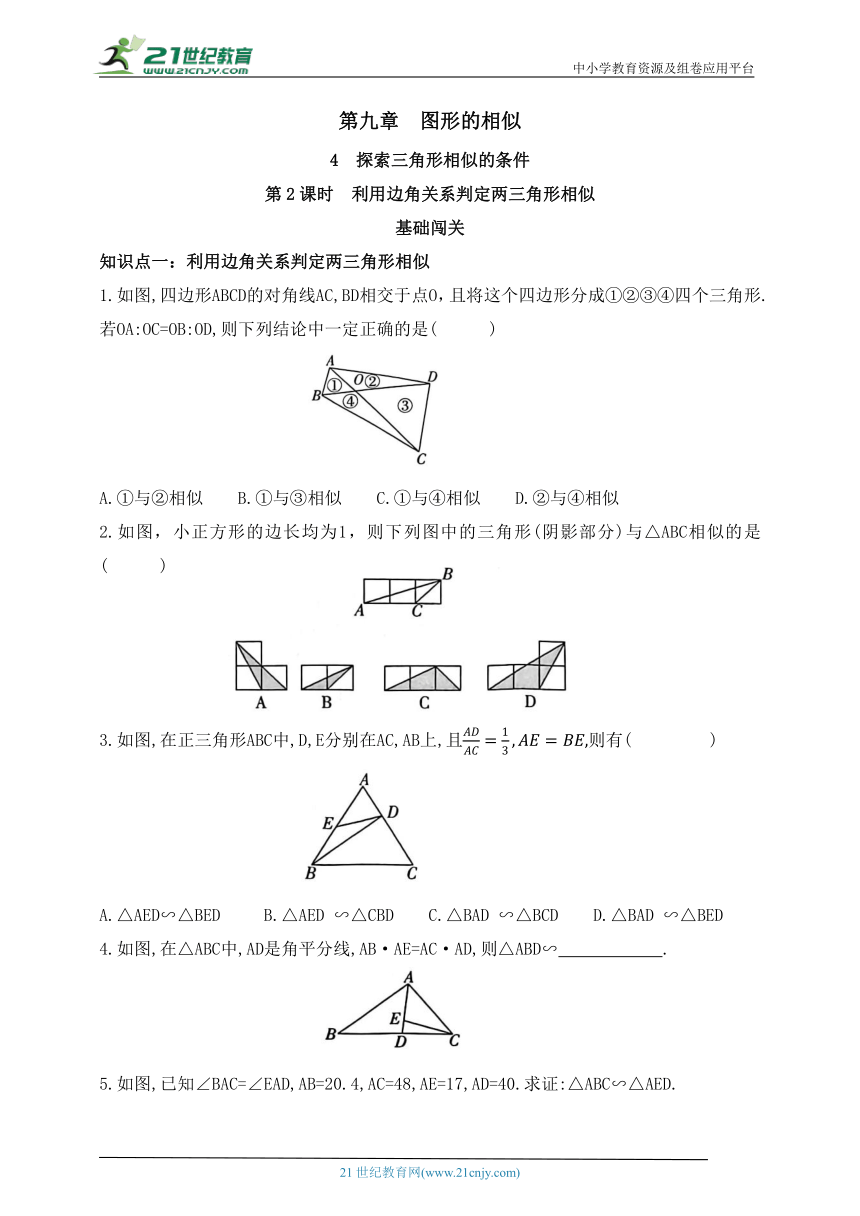
1.如图,四边形ABCD的对角线AC,BD相交于点O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似 C.①与④相似 D.②与④相似
2.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
3.如图,在正三角形ABC中,D,E分别在AC,AB上,且则有( )
A.△AED∽△BED B.△AED ∽△CBD C.△BAD ∽△BCD D.△BAD ∽△BED
4.如图,在△ABC中,AD是角平分线,AB·AE=AC·AD,则△ABD∽ .
5.如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
知识点二:相似三角形判定定理的简单应用
6.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.( 6,3) C.( 6,5) D.( 4,2)
7.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于 .
易错点:忽略分类讨论致错
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的边长分别是3,4及x,那么x的值( )
A.只有1个 B.可以有2个 C.有2个以上但有限 D.有无数个
9.如图所示,在△ABC中,AB=6,AC=4,P 是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和以A,B,C 为顶点的三角形相似,则AQ的长为( )
A.3 B.3 或 C.3 或
能力提升
10.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
11.如图,在△ABC中,AB≠AC.D,E分别为边AB,AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB 与△ADE相似.(只需写出一个)
12.如图,在平行四边形ABCD中,AB=8cm,AD=4cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= cm.
培优创新
13.如图,在正方形ABCD中,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)求证:Rt△ABM∽Rt△MCN.
(2)当M点运动到什么位置时, Rt△ABM∽Rt△AMN 请说明理由.
14.如图,点C,D在线段AB上,且△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB 请说明理由.
(2)当△ACP∽△PDB时,求∠APB的度数.
参考答案
1.B 2.B 3.B 4.△CAE
5.证明:
又∵∠BAC=∠EAD,∴△ABC∽△AED.
6.B 7. 8.B 9.B 10.C 11.示例:DF∥AC 12.7
13.(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°.
∵AM⊥MN,∴∠AMN=90°,∴∠AMB+∠NMC=90°.
∵∠AMB+∠MAB=90°,∴∠MAB=∠NMC,
∴Rt△ABM∽Rt△MCN.
(2)解:当M点运动到BC的中点时,Rt△ABM∽Rt△AMN.
理由:设正方形的边长为2a.∵四边形ABCD为正方形,∴AB=BC=2a,
∽Rt△AMN.
14.解:(1)当 CD =AC·DB时,△ACP∽△PDB.
理由如下:∵△PCD为等边三角形,∴CP=CD=PD,∠PCD=∠PDC=∠CPD=60° ,
∴∠PCA=∠PDB=120°,
即 △PDB.
(2)∵△ACP∽△PDB,∴∠BPD=∠A,
∴∠APC+∠BPD=∠APC+∠A=∠PCD=60°,
∴∠APB =∠APC+∠BPD+∠CPD=60° +60°=120°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用边角关系判定两三角形相似
基础闯关
知识点一:利用边角关系判定两三角形相似
1.如图,四边形ABCD的对角线AC,BD相交于点O,且将这个四边形分成①②③④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是( )
A.①与②相似 B.①与③相似 C.①与④相似 D.②与④相似
2.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
3.如图,在正三角形ABC中,D,E分别在AC,AB上,且则有( )
A.△AED∽△BED B.△AED ∽△CBD C.△BAD ∽△BCD D.△BAD ∽△BED
4.如图,在△ABC中,AD是角平分线,AB·AE=AC·AD,则△ABD∽ .
5.如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ABC∽△AED.
知识点二:相似三角形判定定理的简单应用
6.如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(6,0) B.( 6,3) C.( 6,5) D.( 4,2)
7.如图,点D为△ABC外一点,AD与BC边的交点为E,AE=3,DE=5,BE=4,要使△BDE∽△ACE,且点B,D的对应点为A,C,那么线段CE的长应等于 .
易错点:忽略分类讨论致错
8.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形的边长分别是3,4及x,那么x的值( )
A.只有1个 B.可以有2个 C.有2个以上但有限 D.有无数个
9.如图所示,在△ABC中,AB=6,AC=4,P 是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和以A,B,C 为顶点的三角形相似,则AQ的长为( )
A.3 B.3 或 C.3 或
能力提升
10.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
11.如图,在△ABC中,AB≠AC.D,E分别为边AB,AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: ,可以使得△FDB 与△ADE相似.(只需写出一个)
12.如图,在平行四边形ABCD中,AB=8cm,AD=4cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= cm.
培优创新
13.如图,在正方形ABCD中,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)求证:Rt△ABM∽Rt△MCN.
(2)当M点运动到什么位置时, Rt△ABM∽Rt△AMN 请说明理由.
14.如图,点C,D在线段AB上,且△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB 请说明理由.
(2)当△ACP∽△PDB时,求∠APB的度数.
参考答案
1.B 2.B 3.B 4.△CAE
5.证明:
又∵∠BAC=∠EAD,∴△ABC∽△AED.
6.B 7. 8.B 9.B 10.C 11.示例:DF∥AC 12.7
13.(1)证明:∵四边形ABCD为正方形,∴∠B=∠C=90°.
∵AM⊥MN,∴∠AMN=90°,∴∠AMB+∠NMC=90°.
∵∠AMB+∠MAB=90°,∴∠MAB=∠NMC,
∴Rt△ABM∽Rt△MCN.
(2)解:当M点运动到BC的中点时,Rt△ABM∽Rt△AMN.
理由:设正方形的边长为2a.∵四边形ABCD为正方形,∴AB=BC=2a,
∽Rt△AMN.
14.解:(1)当 CD =AC·DB时,△ACP∽△PDB.
理由如下:∵△PCD为等边三角形,∴CP=CD=PD,∠PCD=∠PDC=∠CPD=60° ,
∴∠PCA=∠PDB=120°,
即 △PDB.
(2)∵△ACP∽△PDB,∴∠BPD=∠A,
∴∠APC+∠BPD=∠APC+∠A=∠PCD=60°,
∴∠APB =∠APC+∠BPD+∠CPD=60° +60°=120°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
