9.4探索三角形相似的条件 第3课时 利用三边关系判定两三角形相似 同步练习(含解析)
文档属性
| 名称 | 9.4探索三角形相似的条件 第3课时 利用三边关系判定两三角形相似 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:09:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用三边关系判定两三角形相似
基础闯关
知识点一:利用三边关系判定两三角形相似
1.△ABC和相似,AB=7,BC=5, 则( )
D.不能确定
2.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1, 乙三角形木框的三边长分别为5,则甲、乙两个三角形( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
3.已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的最短边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似( )
A.2cm,3cm B.4cm,5 cm C.5cm,6cm D.6cm,7 cm
4.已知△ABC的三边长分别为2cm ,5cm,6cm,现将要利用长度为30cm和60cm的细木条各一根,做一个三角形木架与△ABC相似.要求以其中一根作为这个三角形木架的一边,将另一根截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形木架的三边长度分别为( )
A.10cm,25cm,30cm B.10cm,30cm,36cm或10cm,12cm,30cm
C.10cm,30cm,36cm D.10cm,25cm,30cm或12cm,30cm,36cm
知识点二:网格中的相似三角形
5.如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△ABC∽△PQR,则点R 应是甲,乙,丙,丁四点中的( )
A.甲 B.乙 C.丙 D.丁
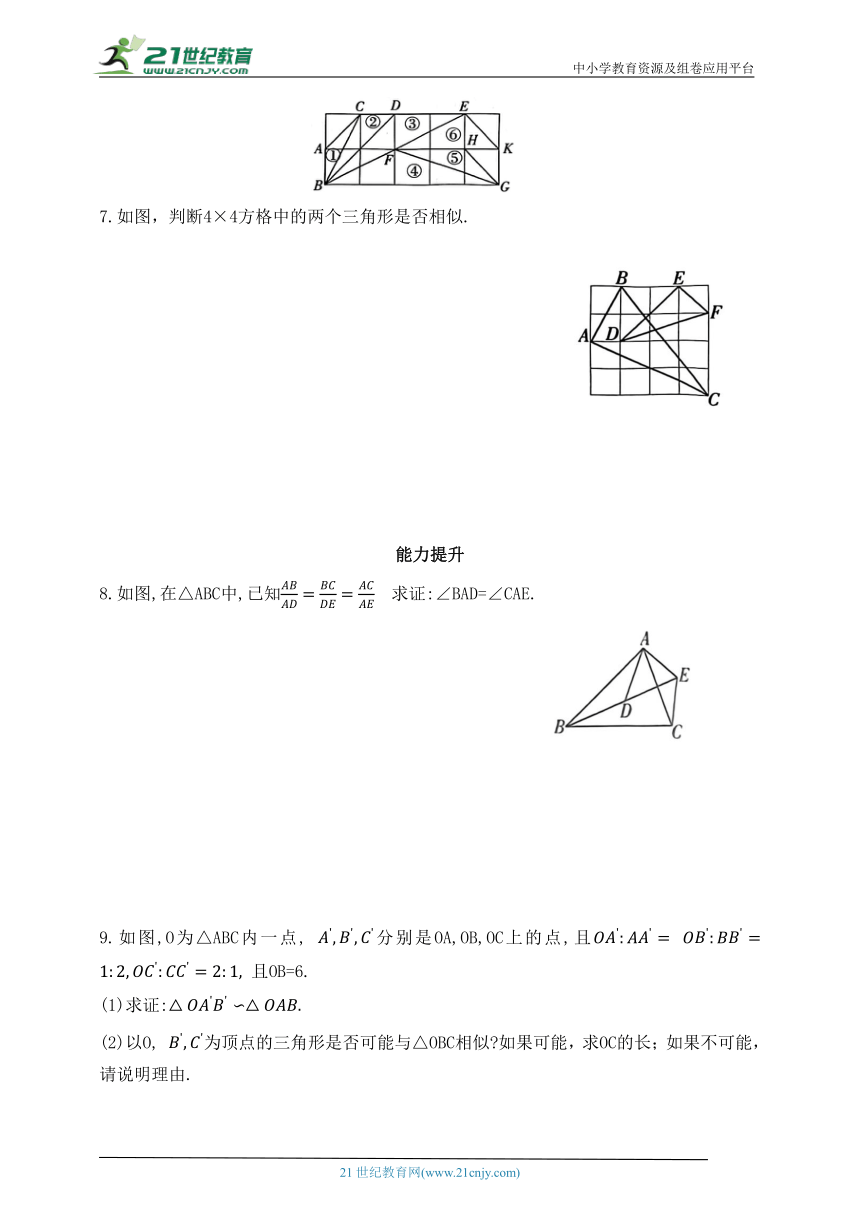
6.如图,在正方形网格中有6个斜三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,
⑥△EKF.在三角形②~⑥中,与①相似的三角形有 .(把你认为正确的三角形的序号都填上)
7.如图,判断4×4方格中的两个三角形是否相似.
能力提升
8.如图,在△ABC中,已知 求证:∠BAD=∠CAE.
9.如图,O为△ABC内一点, 分别是OA,OB,OC上的点,且 且OB=6.
(1)求证:
(2)以O, 为顶点的三角形是否可能与△OBC相似 如果可能,求OC的长;如果不可能,请说明理由.
培优创新
10.如图,在△ABC和中,D, 分别是AB, 上一点
(1)当时,求证:△ABC∽
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当时,判断△ABC与 是否相似,并说明理由.
参考答案
1.B 2.A 3.C 4.D 5.C 6.③④⑤
7.解:设每个小方格的边长为1.由图得
8.证明: ∠DAE,
∴∠BAC-∠DAC= ∠DAE -∠DAC,∴∠BAD=∠CAE.
9.(1)证明:∵
∽△OAB.
(2)解:可能相似.
设则
.要使以O, 为顶点的三角形与△OBC相似,
只要满足 即
10.解:
(2)相似.如图,过点D, 分别作∥∥DE交AC于点E,DE′交A′C′于点E′.
∵DE∥BC,∴△ADE∽△ABC, 同理,
同理,,∴
即
∵DE∥BC,∴∠CED+∠ACB=180°.同理,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
4 探索三角形相似的条件
第2课时 利用三边关系判定两三角形相似
基础闯关
知识点一:利用三边关系判定两三角形相似
1.△ABC和相似,AB=7,BC=5, 则( )
D.不能确定
2.有甲、乙两个三角形木框,甲三角形木框的三边长分别为1, 乙三角形木框的三边长分别为5,则甲、乙两个三角形( )
A.一定相似 B.一定不相似 C.不一定相似 D.无法判断
3.已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的最短边长为4cm,当△DEF 的另两边长是下列哪一组时,这两个三角形相似( )
A.2cm,3cm B.4cm,5 cm C.5cm,6cm D.6cm,7 cm
4.已知△ABC的三边长分别为2cm ,5cm,6cm,现将要利用长度为30cm和60cm的细木条各一根,做一个三角形木架与△ABC相似.要求以其中一根作为这个三角形木架的一边,将另一根截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形木架的三边长度分别为( )
A.10cm,25cm,30cm B.10cm,30cm,36cm或10cm,12cm,30cm
C.10cm,30cm,36cm D.10cm,25cm,30cm或12cm,30cm,36cm
知识点二:网格中的相似三角形
5.如图,若A,B,C,P,Q,甲,乙,丙,丁都是方格纸中的格点,为使△ABC∽△PQR,则点R 应是甲,乙,丙,丁四点中的( )
A.甲 B.乙 C.丙 D.丁
6.如图,在正方形网格中有6个斜三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,
⑥△EKF.在三角形②~⑥中,与①相似的三角形有 .(把你认为正确的三角形的序号都填上)
7.如图,判断4×4方格中的两个三角形是否相似.
能力提升
8.如图,在△ABC中,已知 求证:∠BAD=∠CAE.
9.如图,O为△ABC内一点, 分别是OA,OB,OC上的点,且 且OB=6.
(1)求证:
(2)以O, 为顶点的三角形是否可能与△OBC相似 如果可能,求OC的长;如果不可能,请说明理由.
培优创新
10.如图,在△ABC和中,D, 分别是AB, 上一点
(1)当时,求证:△ABC∽
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当时,判断△ABC与 是否相似,并说明理由.
参考答案
1.B 2.A 3.C 4.D 5.C 6.③④⑤
7.解:设每个小方格的边长为1.由图得
8.证明: ∠DAE,
∴∠BAC-∠DAC= ∠DAE -∠DAC,∴∠BAD=∠CAE.
9.(1)证明:∵
∽△OAB.
(2)解:可能相似.
设则
.要使以O, 为顶点的三角形与△OBC相似,
只要满足 即
10.解:
(2)相似.如图,过点D, 分别作∥∥DE交AC于点E,DE′交A′C′于点E′.
∵DE∥BC,∴△ADE∽△ABC, 同理,
同理,,∴
即
∵DE∥BC,∴∠CED+∠ACB=180°.同理,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
