9.8相似三角形的性质 第1课时 相似三角形对应线段的性质 同步练习(含解析)
文档属性
| 名称 | 9.8相似三角形的性质 第1课时 相似三角形对应线段的性质 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:15:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
8 相似三角形的性质
第1课时 相似三角形对应线段的性质
基础闯关
知识点一:相似三角形边的性质
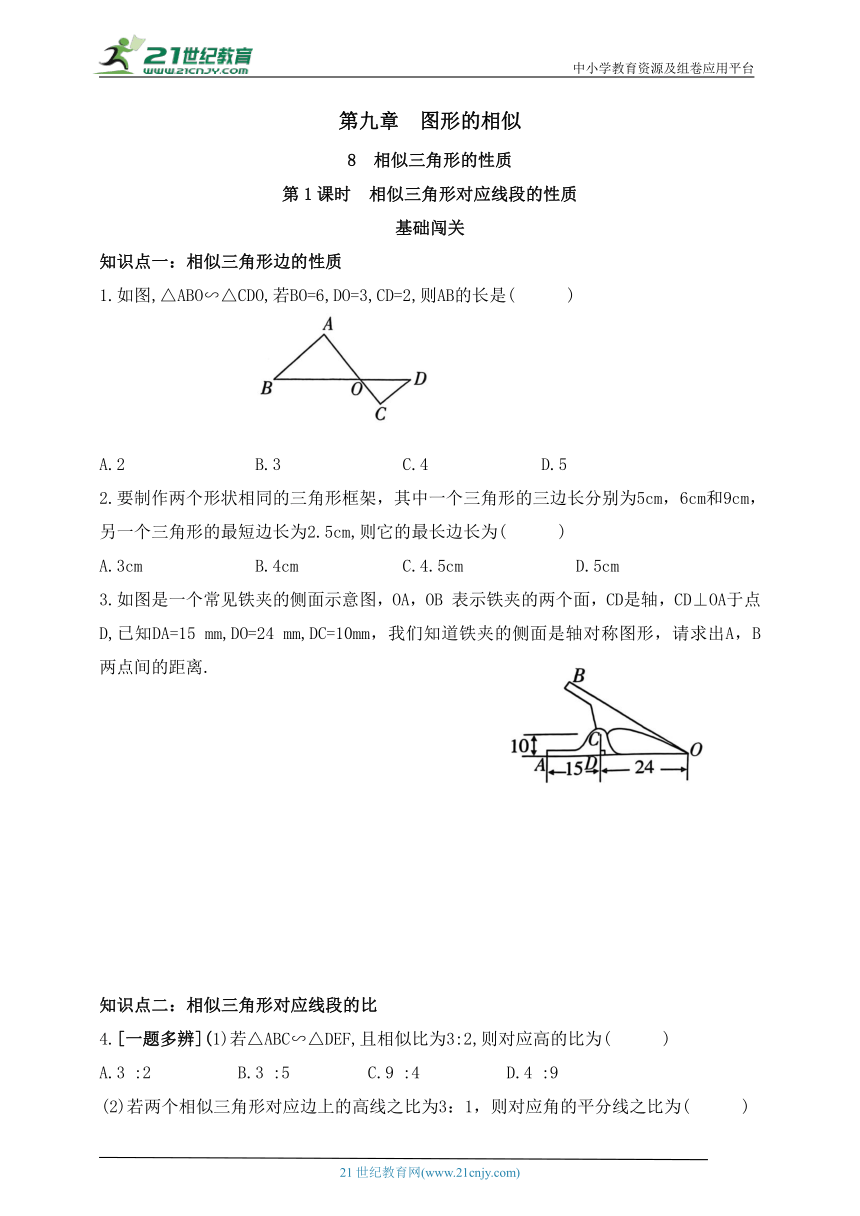
1.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边长为( )
A.3cm B.4cm C.4.5cm D.5cm
3.如图是一个常见铁夹的侧面示意图,OA,OB 表示铁夹的两个面,CD是轴,CD⊥OA于点D,已知DA=15 mm,DO=24 mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A,B两点间的距离.
知识点二:相似三角形对应线段的比
4.[一题多辨](1)若△ABC∽△DEF,且相似比为3:2,则对应高的比为( )
A.3 :2 B.3 :5 C.9 :4 D.4 :9
(2)若两个相似三角形对应边上的高线之比为3:1,则对应角的平分线之比为( )
A.9:1 B.6:1 C.3 :1
5.已知△ABC∽△DEF,若△ABC 与△DEF的相似比为则△ABC与△DEF对应中线的比为( )
6.如图,在6×6的方格纸上有△ABC和△DEF,它们的顶点都在格点上,AG和DH 分别是它们的高,则AG:DH等于( )
A.1:2 B.2:3 C.1:3 D.3:4
7.如图,一等腰三角形底边的长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第________个.
8.如图,AF是△ABC的高,点D,E分别在AB,AC上,且DE∥BC,DE交AF于点G,若DE=6,BC=10,GF=5,求AG的长.
能力提升
9.如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH= .
10.如图,点C,D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC,CD,BD之间的数量关系.
11.如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于点E,交AC的延长线于点F.
(1)求证:△ADF∽△EDB.
(2)求证: CD =DE·DF.
培优创新
12.如图,在矩形ABCD中,对角线AC,BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE分别交BD,CD于点G和点H.
(1)求证: DG =FG·BG.
(2)若AB=5,BC=6,求线段GH的长度.
参考答案
1.C 2.C
3.解:作出示意图,如图所示.连接AB,同时连接OC并延长交AB于点E.
∵铁夹是轴对称图形,故OE是对称轴,
而 即
30mm.
即A,B两点间的距离为30mm.
4.(1)A (2)C 5.A 6.A 7.5
8.解:∵DE∥BC,∴△ADG∽△ABF,△ADE∽△ABC,
解得AG=7.5.
9.1
10.解:(1)∵△PCD是等边三角形,∴∠PCD=60°,∴∠A +∠APC=60°.
∵△ACP∽△PDB,∴∠APC=∠B,∴∠A+∠B=60°,∴∠APB=120°.
(2)∵△ACP ∽△
11.证明:(1)在Rt△ABC中,∠B+∠A=90°.
∵DF⊥AB,∴∠BDE = ∠ADF =90°,∴∠A + ∠F =90°,∴∠B=∠F,∴△ADF∽△EDB. (2)由(1)可知△ADF∽△EDB,∠B=∠F.
∵CD是Rt△ABC斜边AB上的中线,∴CD=AD=DB,∴∠DCE=∠B,
∴CD =DE·DF.
12.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴△ADG∽△EBG,∴
∵四边形ACED是平行四边形,
∴
(2)解:∵四边形ACED为平行四边形,AE,CD相交于点H ,
在Rt△ADH中, AH =AD +DH ,∴AH=∴AE=13.
又∵△ADG∽△EBG,∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
8 相似三角形的性质
第1课时 相似三角形对应线段的性质
基础闯关
知识点一:相似三角形边的性质
1.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
A.2 B.3 C.4 D.5
2.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和9cm,另一个三角形的最短边长为2.5cm,则它的最长边长为( )
A.3cm B.4cm C.4.5cm D.5cm
3.如图是一个常见铁夹的侧面示意图,OA,OB 表示铁夹的两个面,CD是轴,CD⊥OA于点D,已知DA=15 mm,DO=24 mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A,B两点间的距离.
知识点二:相似三角形对应线段的比
4.[一题多辨](1)若△ABC∽△DEF,且相似比为3:2,则对应高的比为( )
A.3 :2 B.3 :5 C.9 :4 D.4 :9
(2)若两个相似三角形对应边上的高线之比为3:1,则对应角的平分线之比为( )
A.9:1 B.6:1 C.3 :1
5.已知△ABC∽△DEF,若△ABC 与△DEF的相似比为则△ABC与△DEF对应中线的比为( )
6.如图,在6×6的方格纸上有△ABC和△DEF,它们的顶点都在格点上,AG和DH 分别是它们的高,则AG:DH等于( )
A.1:2 B.2:3 C.1:3 D.3:4
7.如图,一等腰三角形底边的长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第________个.
8.如图,AF是△ABC的高,点D,E分别在AB,AC上,且DE∥BC,DE交AF于点G,若DE=6,BC=10,GF=5,求AG的长.
能力提升
9.如图,在△ABC中,D,E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=6,则DH= .
10.如图,点C,D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC,CD,BD之间的数量关系.
11.如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于点E,交AC的延长线于点F.
(1)求证:△ADF∽△EDB.
(2)求证: CD =DE·DF.
培优创新
12.如图,在矩形ABCD中,对角线AC,BD相交于点F,延长BC到点E,使得四边形ACED是一个平行四边形,平行四边形对角线AE分别交BD,CD于点G和点H.
(1)求证: DG =FG·BG.
(2)若AB=5,BC=6,求线段GH的长度.
参考答案
1.C 2.C
3.解:作出示意图,如图所示.连接AB,同时连接OC并延长交AB于点E.
∵铁夹是轴对称图形,故OE是对称轴,
而 即
30mm.
即A,B两点间的距离为30mm.
4.(1)A (2)C 5.A 6.A 7.5
8.解:∵DE∥BC,∴△ADG∽△ABF,△ADE∽△ABC,
解得AG=7.5.
9.1
10.解:(1)∵△PCD是等边三角形,∴∠PCD=60°,∴∠A +∠APC=60°.
∵△ACP∽△PDB,∴∠APC=∠B,∴∠A+∠B=60°,∴∠APB=120°.
(2)∵△ACP ∽△
11.证明:(1)在Rt△ABC中,∠B+∠A=90°.
∵DF⊥AB,∴∠BDE = ∠ADF =90°,∴∠A + ∠F =90°,∴∠B=∠F,∴△ADF∽△EDB. (2)由(1)可知△ADF∽△EDB,∠B=∠F.
∵CD是Rt△ABC斜边AB上的中线,∴CD=AD=DB,∴∠DCE=∠B,
∴CD =DE·DF.
12.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴△ADG∽△EBG,∴
∵四边形ACED是平行四边形,
∴
(2)解:∵四边形ACED为平行四边形,AE,CD相交于点H ,
在Rt△ADH中, AH =AD +DH ,∴AH=∴AE=13.
又∵△ADG∽△EBG,∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
