9.9利用位似放缩图形 第1课时 位似图形 同步练习(含解析)
文档属性
| 名称 | 9.9利用位似放缩图形 第1课时 位似图形 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:15:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
9 利用位似放缩图形
第1课时 位似图形
基础闯关
知识点一:位似的定义
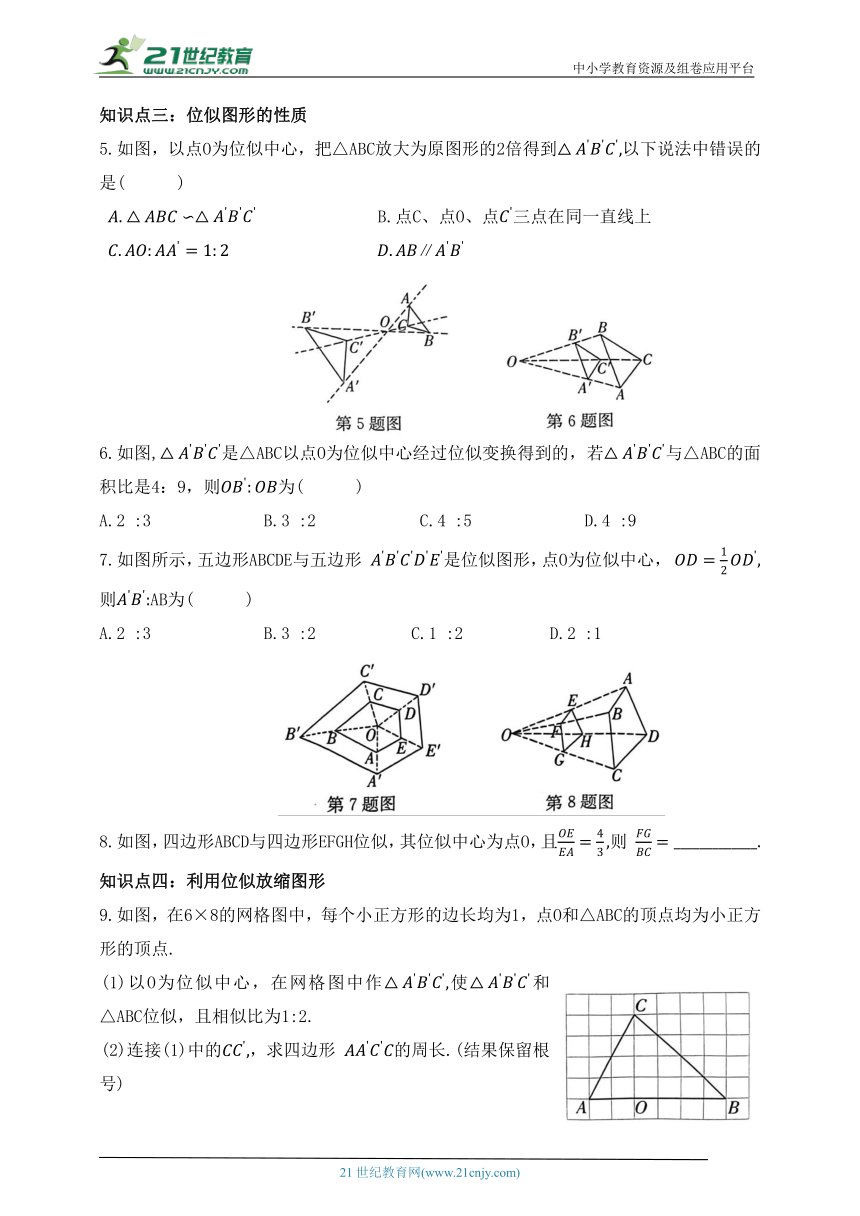
1.下列各组图形中,不是位似图形的是( )
2.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
知识点二:位似中心
3.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
4.如图,在6×7的网格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
A.P B.P C.P D.P
知识点三:位似图形的性质
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到以下说法中错误的是( )
B.点C、点O、点三点在同一直线上
∥
6.如图,是△ABC以点O为位似中心经过位似变换得到的,若与△ABC的面积比是4:9,则为( )
A.2 :3 B.3 :2 C.4 :5 D.4 :9
7.如图所示,五边形ABCDE与五边形 是位似图形,点O为位似中心, 则AB为( )
A.2 :3 B.3 :2 C.1 :2 D.2 :1
8.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且则
知识点四:利用位似放缩图形
9.如图,在6×8的网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作使和△ABC位似,且相似比为1:2.
(2)连接(1)中的,求四边形 的周长.(结果保留根号)
能力提升
10.如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF.
(1)图中有哪几对位似三角形
(2)若AB=2,CD=3,求EF的长.
11.如图,已知 ∥∥∥
(1)求证:四边形BCDE与四边形位似.
(2)若求
培优创新
12.如图所示,在矩形ABCD 中,对角线AC,BD相交于点O.
(1)过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC 与△FGC是位似图形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定 的值.
参考答案
1.B 2.A 3.D 4.C 5.C 6.A 7.D
9.解:(1)如图所示,即为所求作的三角形.
(2)根据勾股定理得 ∴四边形的周长为
10.解:(1)△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形.
(2)∵△BFE∽△BDC,
11.(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,∴
又∵四边形BCDE与四边形 对应顶点的连线相交于一点A,
∴四边形BCDE与四边形位似.
(2)解:∵∴,∴四边形BCDE与四边形B′C′D′E′的相似比为
∵,∴
12.解:(1)是位似图形.理由如下:∵FG⊥BC,AB⊥BC,∴FG∥AB,∴△ABC∽△FGC,
△ABC与△FGC对应顶点的连线相交于一点,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C.
∥
则△ABC与△FGC的相似比为3.
(2)由(1)得∥
又∵
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章 图形的相似
9 利用位似放缩图形
第1课时 位似图形
基础闯关
知识点一:位似的定义
1.下列各组图形中,不是位似图形的是( )
2.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
知识点二:位似中心
3.图中两个四边形是位似图形,它们的位似中心是( )
A.点M B.点N C.点O D.点P
4.如图,在6×7的网格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
A.P B.P C.P D.P
知识点三:位似图形的性质
5.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到以下说法中错误的是( )
B.点C、点O、点三点在同一直线上
∥
6.如图,是△ABC以点O为位似中心经过位似变换得到的,若与△ABC的面积比是4:9,则为( )
A.2 :3 B.3 :2 C.4 :5 D.4 :9
7.如图所示,五边形ABCDE与五边形 是位似图形,点O为位似中心, 则AB为( )
A.2 :3 B.3 :2 C.1 :2 D.2 :1
8.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且则
知识点四:利用位似放缩图形
9.如图,在6×8的网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作使和△ABC位似,且相似比为1:2.
(2)连接(1)中的,求四边形 的周长.(结果保留根号)
能力提升
10.如图,F在BD上,BC,AD相交于点E,且AB∥CD∥EF.
(1)图中有哪几对位似三角形
(2)若AB=2,CD=3,求EF的长.
11.如图,已知 ∥∥∥
(1)求证:四边形BCDE与四边形位似.
(2)若求
培优创新
12.如图所示,在矩形ABCD 中,对角线AC,BD相交于点O.
(1)过点O作OE⊥BC于点E,连接DE交OC于点F,作FG⊥BC于点G,则△ABC 与△FGC是位似图形吗 若是,请说出位似中心,并求出相似比;若不是,请说明理由.
(2)连接DG交AC于点H,作HI⊥BC于I,试确定 的值.
参考答案
1.B 2.A 3.D 4.C 5.C 6.A 7.D
9.解:(1)如图所示,即为所求作的三角形.
(2)根据勾股定理得 ∴四边形的周长为
10.解:(1)△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形.
(2)∵△BFE∽△BDC,
11.(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,∴
又∵四边形BCDE与四边形 对应顶点的连线相交于一点A,
∴四边形BCDE与四边形位似.
(2)解:∵∴,∴四边形BCDE与四边形B′C′D′E′的相似比为
∵,∴
12.解:(1)是位似图形.理由如下:∵FG⊥BC,AB⊥BC,∴FG∥AB,∴△ABC∽△FGC,
△ABC与△FGC对应顶点的连线相交于一点,对应边互相平行或重合,
∴△ABC与△FGC是位似图形,位似中心是点C.
∥
则△ABC与△FGC的相似比为3.
(2)由(1)得∥
又∵
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
