专项训练 作平行线构造平行线分线段成比例模型解决问题(含答案)
文档属性
| 名称 | 专项训练 作平行线构造平行线分线段成比例模型解决问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:17:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
作平行线构造平行线分线段成比例模型解决问题
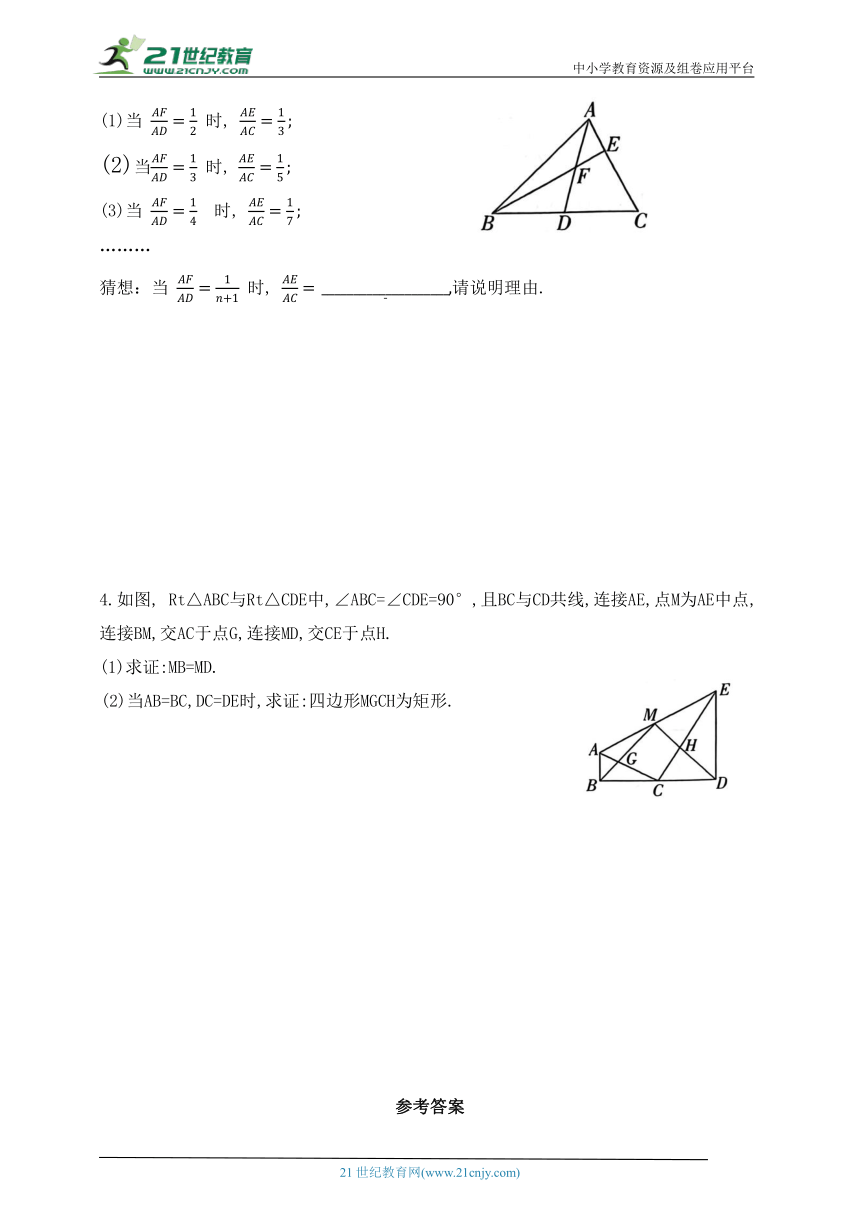
1.如图,在△ABC中,M为AC边的中点,E为AB上一点,且AB=4AE,连接EM并延长,交BC的延长线于点D,求证:BC=2CD.
2.对于平行线,我们有这样的结论:如图①,AB∥CD,AD,BC交于点O,则 请利用该结论解答下面的问题:
如图②,在△ABC 中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC 的长.
3.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
(1)当 时,
(2)当 时,
(3)当 时,
………
猜想:当 时, 请说明理由.
4.如图, Rt△ABC与Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,连接AE,点M为AE中点,连接BM,交AC于点G,连接MD,交CE于点H.
(1)求证:MB=MD.
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
参考答案
1.证明:如图,过点C作CF∥DE,交AB于点F.
∵ME∥
∵M为AC边的中点,∴AM=MC,
∴BC=2CD.
2.解:如图,过点C作CE∥AB,交AD的延长线于点E,则
又∵BD=2DC,AD=2,∴DE=1.
∵CE∥AB,∴∠E=∠BAD=75°.
又∵∠CAD=30°,∴∠ACE=75°,∴AC=AE=AD+DE=3.
3.解: 理由如下:如图,过点D作DG∥BE,交AC于点G,
则
是△ABC的中线,
4.证明:(1)如图,延长BM交DE的延长线于点N.
∥
∵点M为AE中点,∴AM=ME,∴BM=MN,∴DM为Rt△BDN的斜边上的中线,∴MB=MD.
(2)由(1)△ABM≌△ENM,∴AB=NE.
∵AB=BC,DC=DE,∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,∴DM⊥BN,∠DBM=∠N=45° ,∠BMD =90°.
∵AB=BC,DC = DE,∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=45°,∴∠CED=∠N,∠ACB=∠BDM,∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形.
∵∠BMD=90°,∴四边形MGCH为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
作平行线构造平行线分线段成比例模型解决问题
1.如图,在△ABC中,M为AC边的中点,E为AB上一点,且AB=4AE,连接EM并延长,交BC的延长线于点D,求证:BC=2CD.
2.对于平行线,我们有这样的结论:如图①,AB∥CD,AD,BC交于点O,则 请利用该结论解答下面的问题:
如图②,在△ABC 中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC 的长.
3.如图,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论:
(1)当 时,
(2)当 时,
(3)当 时,
………
猜想:当 时, 请说明理由.
4.如图, Rt△ABC与Rt△CDE中,∠ABC=∠CDE=90°,且BC与CD共线,连接AE,点M为AE中点,连接BM,交AC于点G,连接MD,交CE于点H.
(1)求证:MB=MD.
(2)当AB=BC,DC=DE时,求证:四边形MGCH为矩形.
参考答案
1.证明:如图,过点C作CF∥DE,交AB于点F.
∵ME∥
∵M为AC边的中点,∴AM=MC,
∴BC=2CD.
2.解:如图,过点C作CE∥AB,交AD的延长线于点E,则
又∵BD=2DC,AD=2,∴DE=1.
∵CE∥AB,∴∠E=∠BAD=75°.
又∵∠CAD=30°,∴∠ACE=75°,∴AC=AE=AD+DE=3.
3.解: 理由如下:如图,过点D作DG∥BE,交AC于点G,
则
是△ABC的中线,
4.证明:(1)如图,延长BM交DE的延长线于点N.
∥
∵点M为AE中点,∴AM=ME,∴BM=MN,∴DM为Rt△BDN的斜边上的中线,∴MB=MD.
(2)由(1)△ABM≌△ENM,∴AB=NE.
∵AB=BC,DC=DE,∴BD=BC+CD=AB+DE=NE+DE=DN,
∴△BDN为等腰直角三角形,∴DM⊥BN,∠DBM=∠N=45° ,∠BMD =90°.
∵AB=BC,DC = DE,∴Rt△ABC和Rt△CDE都是等腰直角三角形,
∴∠CED=∠ACB=45°,∴∠CED=∠N,∠ACB=∠BDM,∴CE∥BN,AC∥DM,
∴四边形MGCH为平行四边形.
∵∠BMD=90°,∴四边形MGCH为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
