专项训练 “三垂直”模型(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
专项训练
“三垂直”模型
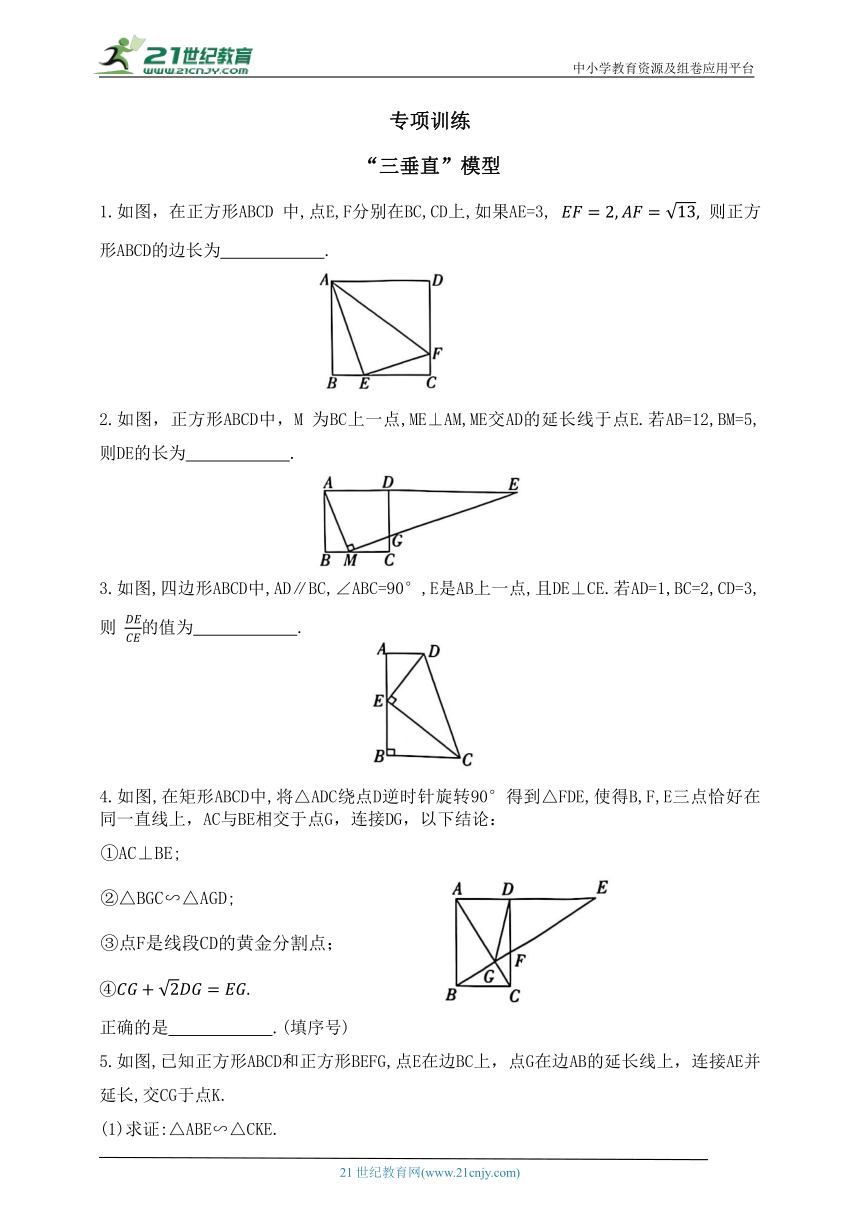
1.如图,在正方形ABCD 中,点E,F分别在BC,CD上,如果AE=3, 则正方形ABCD的边长为 .
2.如图,正方形ABCD中,M 为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为 .
3.如图,四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则 的值为 .
4.如图,在矩形ABCD中,将△ADC绕点D逆时针旋转90°得到△FDE,使得B,F,E三点恰好在同一直线上,AC与BE相交于点G,连接DG,以下结论:
①AC⊥BE;
②△BGC∽△AGD;
③点F是线段CD的黄金分割点;
④
正确的是 .(填序号)
5.如图,已知正方形ABCD和正方形BEFG,点E在边BC上,点G在边AB的延长线上,连接AE并延长,交CG于点K.
(1)求证:△ABE∽△CKE.
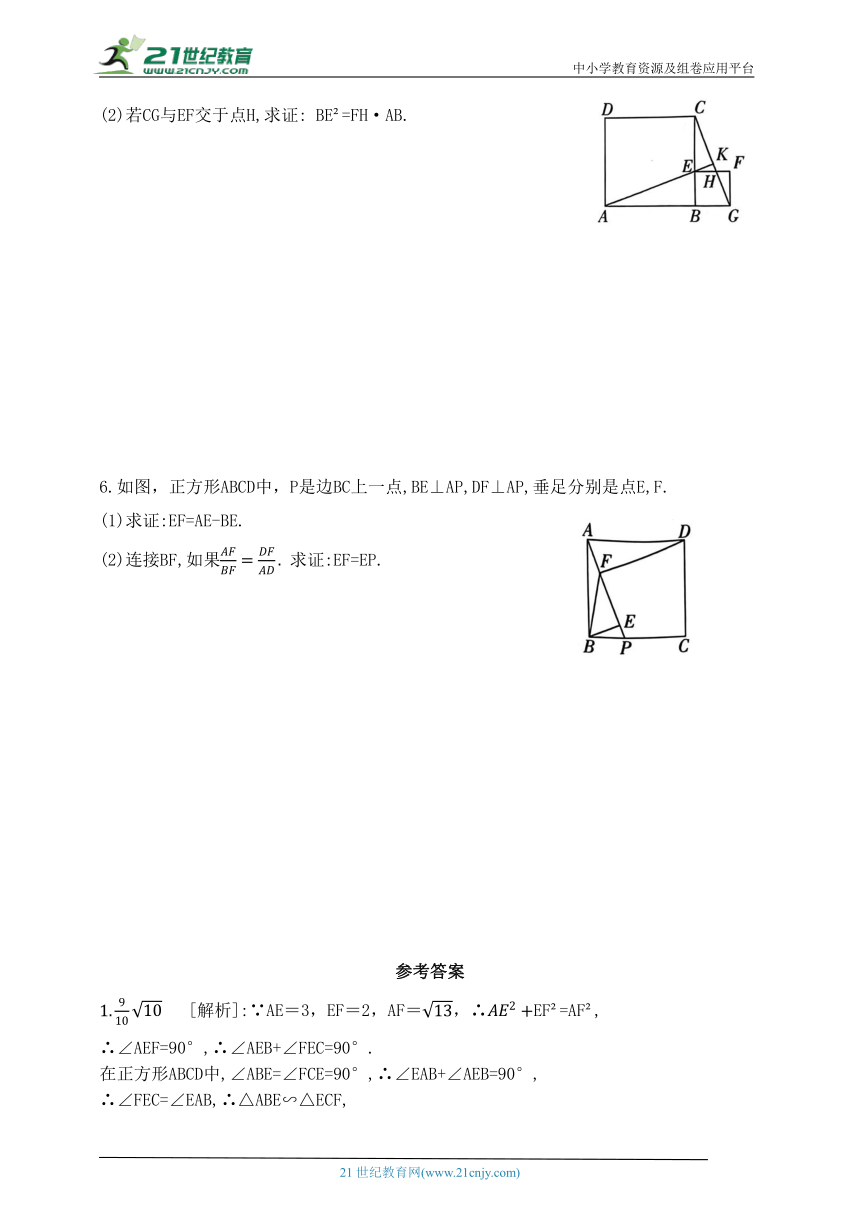
(2)若CG与EF交于点H,求证: BE =FH·AB.
6.如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E,F.
(1)求证:EF=AE-BE.
(2)连接BF,如果 求证:EF=EP.
参考答案
[解析]:∵AE=3,EF=2,AF=,∴EF =AF ,
∴∠AEF=90°,∴∠AEB+∠FEC=90°.
在正方形ABCD中,∠ABE=∠FCE=90°,∴∠EAB+∠AEB=90°,
∴∠FEC=∠EAB,∴△ABE∽△ECF,
∴EC:AB=EF:AE=2:3,即
[解析]∵四边形ABCD是正方形,AB=12,BM=5,∴MC=12-5=7.
∵ME ⊥AM,∴∠AME=90°,∴∠AMB+∠CMG=90°.
∵∠B=∠C=90°,∴∠AMB+∠BAM=90°,∴∠BAM=∠CMG,∴△ABM∽△MCG,
即解得
∵AE∥BC,∴∠E=∠CMG,∠EDG=∠C, 即 解得DE
[解析]过点D作DH⊥BC.∵AD=1,BC=2,∴CH
∥BC,∠ABC=90°,∴∠A=90°.∵DE⊥CE,∴∠AED+∠BEC=90°.
∵∠AED+∠ADE=90°,∴∠ADE=∠BEC,∴△ADE∽△BEC,∴
设BE=x,则 即 解得
4.①③④ [解析]四边形ABCD是矩形,∴AD=BC,∠BAD=∠ADC=90°,AD∥BC,
∴∠DAC+∠ACD=90°.
由旋转得△ADC≌△FDE,∴AD=DF,DC=DE,∠DCA=∠E,∠ADC=∠FDE=90°,
∴∠DAC+∠E=90°,∴∠AGE=180°-(∠DAC+∠E)=90°,∴AC⊥BE,故①正确.
∵AC⊥BE,∴∠AGE=∠BGC=90°,∴△BGC是直角三角形,△AGD是锐角三角形,
∴△BGC与△AGD不相似,故②不正确.
∵∠ADC=∠FDE=90°,∴∠ADC+∠FDE=180°,∴点A,D,E三点共线.
∵AD∥BC,∴∠E=∠EBC,∠EDF=∠BCF,∴△BCF∽△
点F是线段CD的黄金分割点,故③正确.
如图,在EG上截取=CG,连接DG′.
∵DC=DE,∠DCA=∠E,∴△GCD≌
即
是等腰直角三角形,
故④正确.
5.证明:(1)∵四边形ABCD是正方形,∴AB=CB,∠ABC =90°.
∵四边形BEFG是正方形,∴FG=BG=BE,∠CBG=90°,∴∠ABE=∠CBG.
在△ABE和△CBG中, =∠ECK.
又∵∠AEB=∠CEK,∴△ABE∽△CKE.
(2)由题意得∠CEF=∠F=∠ABE=90°,∴FG∥BC,∴∠ECK=∠FGH.
∵∠BAE=∠ECK,∴∠BAE=
6.证明:(1)如图,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠1+∠2=90°.
∵BE ⊥AP,DF ⊥AP,∴∠BEA=∠AFD=90°,∴∠2+∠3=90°,∴∠1=∠3.
在△ABE和△DAF中 △DAF,∴BE=AF,∴EF=AE-AF=AE-BE.
(2)如图,∴Rt△BEF∽△DFA,∴∠4=∠3.
∵∠1=∠3,∴∠4=∠1.∵∠5+∠APB=∠1+∠APB=90°,∴∠5=∠1,
∴∠4=∠5,即BE平分∠FBP.
∵BE⊥FP,∴EF=EP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
“三垂直”模型
1.如图,在正方形ABCD 中,点E,F分别在BC,CD上,如果AE=3, 则正方形ABCD的边长为 .
2.如图,正方形ABCD中,M 为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为 .
3.如图,四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则 的值为 .
4.如图,在矩形ABCD中,将△ADC绕点D逆时针旋转90°得到△FDE,使得B,F,E三点恰好在同一直线上,AC与BE相交于点G,连接DG,以下结论:
①AC⊥BE;
②△BGC∽△AGD;
③点F是线段CD的黄金分割点;
④
正确的是 .(填序号)
5.如图,已知正方形ABCD和正方形BEFG,点E在边BC上,点G在边AB的延长线上,连接AE并延长,交CG于点K.
(1)求证:△ABE∽△CKE.
(2)若CG与EF交于点H,求证: BE =FH·AB.
6.如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E,F.
(1)求证:EF=AE-BE.
(2)连接BF,如果 求证:EF=EP.
参考答案
[解析]:∵AE=3,EF=2,AF=,∴EF =AF ,
∴∠AEF=90°,∴∠AEB+∠FEC=90°.
在正方形ABCD中,∠ABE=∠FCE=90°,∴∠EAB+∠AEB=90°,
∴∠FEC=∠EAB,∴△ABE∽△ECF,
∴EC:AB=EF:AE=2:3,即
[解析]∵四边形ABCD是正方形,AB=12,BM=5,∴MC=12-5=7.
∵ME ⊥AM,∴∠AME=90°,∴∠AMB+∠CMG=90°.
∵∠B=∠C=90°,∴∠AMB+∠BAM=90°,∴∠BAM=∠CMG,∴△ABM∽△MCG,
即解得
∵AE∥BC,∴∠E=∠CMG,∠EDG=∠C, 即 解得DE
[解析]过点D作DH⊥BC.∵AD=1,BC=2,∴CH
∥BC,∠ABC=90°,∴∠A=90°.∵DE⊥CE,∴∠AED+∠BEC=90°.
∵∠AED+∠ADE=90°,∴∠ADE=∠BEC,∴△ADE∽△BEC,∴
设BE=x,则 即 解得
4.①③④ [解析]四边形ABCD是矩形,∴AD=BC,∠BAD=∠ADC=90°,AD∥BC,
∴∠DAC+∠ACD=90°.
由旋转得△ADC≌△FDE,∴AD=DF,DC=DE,∠DCA=∠E,∠ADC=∠FDE=90°,
∴∠DAC+∠E=90°,∴∠AGE=180°-(∠DAC+∠E)=90°,∴AC⊥BE,故①正确.
∵AC⊥BE,∴∠AGE=∠BGC=90°,∴△BGC是直角三角形,△AGD是锐角三角形,
∴△BGC与△AGD不相似,故②不正确.
∵∠ADC=∠FDE=90°,∴∠ADC+∠FDE=180°,∴点A,D,E三点共线.
∵AD∥BC,∴∠E=∠EBC,∠EDF=∠BCF,∴△BCF∽△
点F是线段CD的黄金分割点,故③正确.
如图,在EG上截取=CG,连接DG′.
∵DC=DE,∠DCA=∠E,∴△GCD≌
即
是等腰直角三角形,
故④正确.
5.证明:(1)∵四边形ABCD是正方形,∴AB=CB,∠ABC =90°.
∵四边形BEFG是正方形,∴FG=BG=BE,∠CBG=90°,∴∠ABE=∠CBG.
在△ABE和△CBG中, =∠ECK.
又∵∠AEB=∠CEK,∴△ABE∽△CKE.
(2)由题意得∠CEF=∠F=∠ABE=90°,∴FG∥BC,∴∠ECK=∠FGH.
∵∠BAE=∠ECK,∴∠BAE=
6.证明:(1)如图,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠1+∠2=90°.
∵BE ⊥AP,DF ⊥AP,∴∠BEA=∠AFD=90°,∴∠2+∠3=90°,∴∠1=∠3.
在△ABE和△DAF中 △DAF,∴BE=AF,∴EF=AE-AF=AE-BE.
(2)如图,∴Rt△BEF∽△DFA,∴∠4=∠3.
∵∠1=∠3,∴∠4=∠1.∵∠5+∠APB=∠1+∠APB=90°,∴∠5=∠1,
∴∠4=∠5,即BE平分∠FBP.
∵BE⊥FP,∴EF=EP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
