专项训练 求比值及证明比例式或等积式的技巧(含答案)
文档属性
| 名称 | 专项训练 求比值及证明比例式或等积式的技巧(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:20:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
求比值及证明比例式或等积式的技巧
技巧一:构造平行线求比值
1.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND 的值.
技巧二:寻找相似三角形证明比例中项
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,F是AB中点,连接EF交AD于点G.
(1)求证: AD =AB ·AE.
(2)若AB=3,AE=2,求的值.
技巧三:利用两次相似证明比例式或等积式
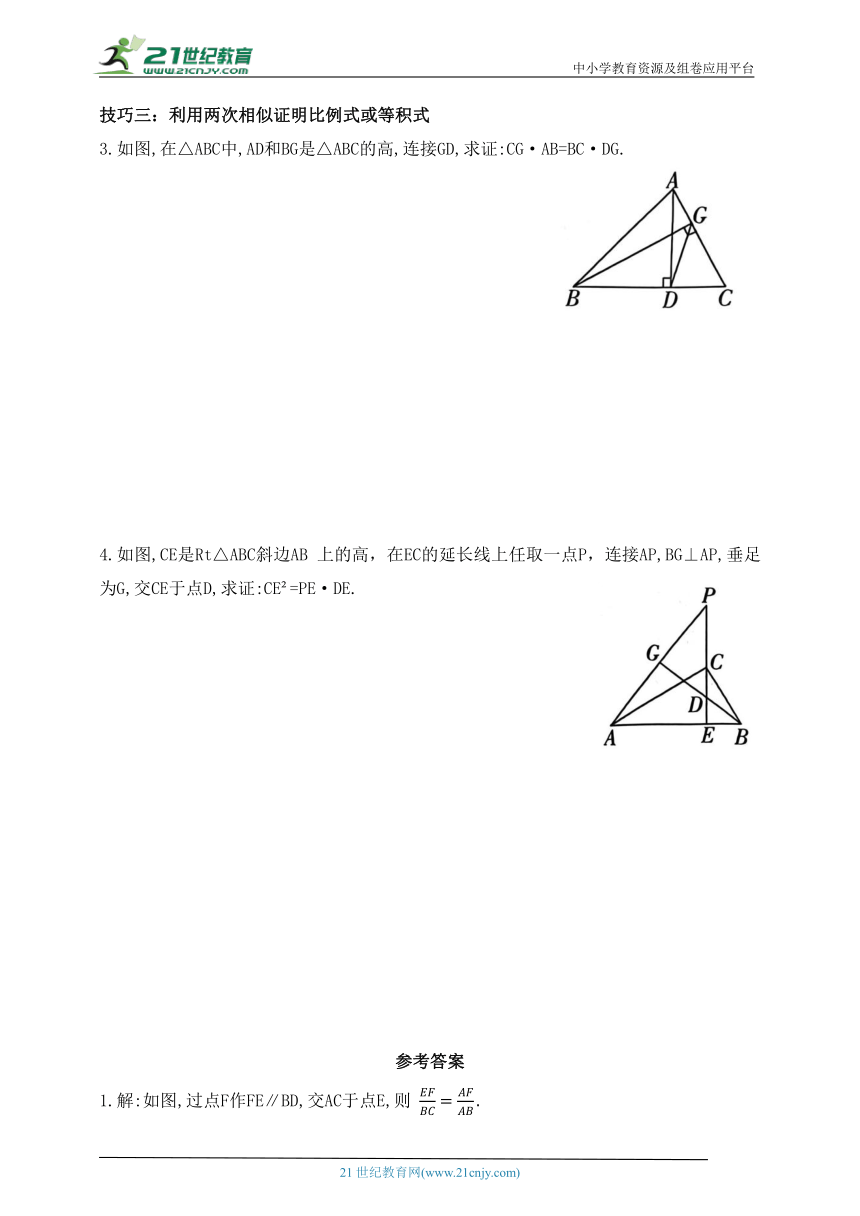
3.如图,在△ABC中,AD和BG是△ABC的高,连接GD,求证:CG·AB=BC·DG.
4.如图,CE是Rt△ABC斜边AB 上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP,垂足为G,交CE于点D,求证:CE =PE·DE.
参考答案
1.解:如图,过点F作FE∥BD,交AC于点E,则
即FE=
即FN:ND=2:3.
2.(1)证明:∵AD⊥BC于点D,DE⊥AC于点E,∴∠ADC=∠AED=90°.
∵∠DAE=∠DAC,∴△DAE∽△CAD,
AB·AE.
(2)解:如图,连接DF.∵AB=3,∠ADB=90°,F是AB中点,
3.证明:∵在△ABC中,AD和BG是△ABC的高,∴∠BGC =∠ADC=90°.
又∵∠C=∠C,∴△ADC∽△BGC, 即
又∵∠C=∠C,∴△GDC∽ △即CG·AB=BC·DG.
4.证明:∵∠ACB=90°,CE⊥AB,∴∠ACE+∠BCE=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCE,∴Rt△ACE
又∵BG⊥AP,CE ⊥AB,∴∠DEB=∠DGP=∠PEA =90°.
∵∠PDG=∠BDE,∴∠P=∠DBE,∴△AEP ∽△
PE ·DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
求比值及证明比例式或等积式的技巧
技巧一:构造平行线求比值
1.如图,已知点F在AB上,且AF:BF=1:2,点D是BC延长线上一点,BC:CD=2:1,连接FD与AC交于点N,求FN:ND 的值.
技巧二:寻找相似三角形证明比例中项
2.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,F是AB中点,连接EF交AD于点G.
(1)求证: AD =AB ·AE.
(2)若AB=3,AE=2,求的值.
技巧三:利用两次相似证明比例式或等积式
3.如图,在△ABC中,AD和BG是△ABC的高,连接GD,求证:CG·AB=BC·DG.
4.如图,CE是Rt△ABC斜边AB 上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP,垂足为G,交CE于点D,求证:CE =PE·DE.
参考答案
1.解:如图,过点F作FE∥BD,交AC于点E,则
即FE=
即FN:ND=2:3.
2.(1)证明:∵AD⊥BC于点D,DE⊥AC于点E,∴∠ADC=∠AED=90°.
∵∠DAE=∠DAC,∴△DAE∽△CAD,
AB·AE.
(2)解:如图,连接DF.∵AB=3,∠ADB=90°,F是AB中点,
3.证明:∵在△ABC中,AD和BG是△ABC的高,∴∠BGC =∠ADC=90°.
又∵∠C=∠C,∴△ADC∽△BGC, 即
又∵∠C=∠C,∴△GDC∽ △即CG·AB=BC·DG.
4.证明:∵∠ACB=90°,CE⊥AB,∴∠ACE+∠BCE=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCE,∴Rt△ACE
又∵BG⊥AP,CE ⊥AB,∴∠DEB=∠DGP=∠PEA =90°.
∵∠PDG=∠BDE,∴∠P=∠DBE,∴△AEP ∽△
PE ·DE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
