专项训练 相似三角形的实际应用(含答案)
文档属性
| 名称 | 专项训练 相似三角形的实际应用(含答案) | 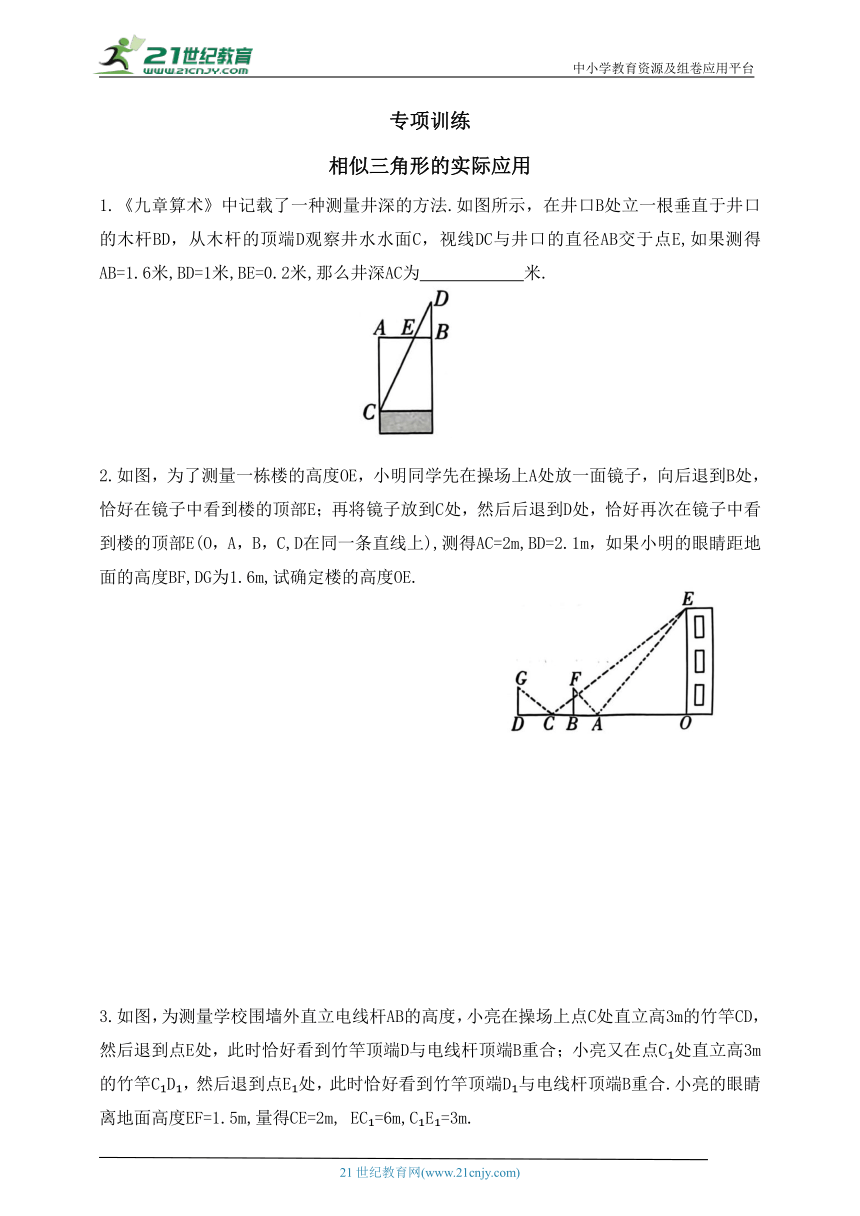 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:24:09 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
相似三角形的实际应用
1.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水面C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为 米.
2.如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2m,BD=2.1m,如果小明的眼睛距地面的高度BF,DG为1.6m,试确定楼的高度OE.
3.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C 处直立高3m的竹竿C D ,然后退到点E 处,此时恰好看到竹竿顶端D 与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m, EC =6m,C E =3m.
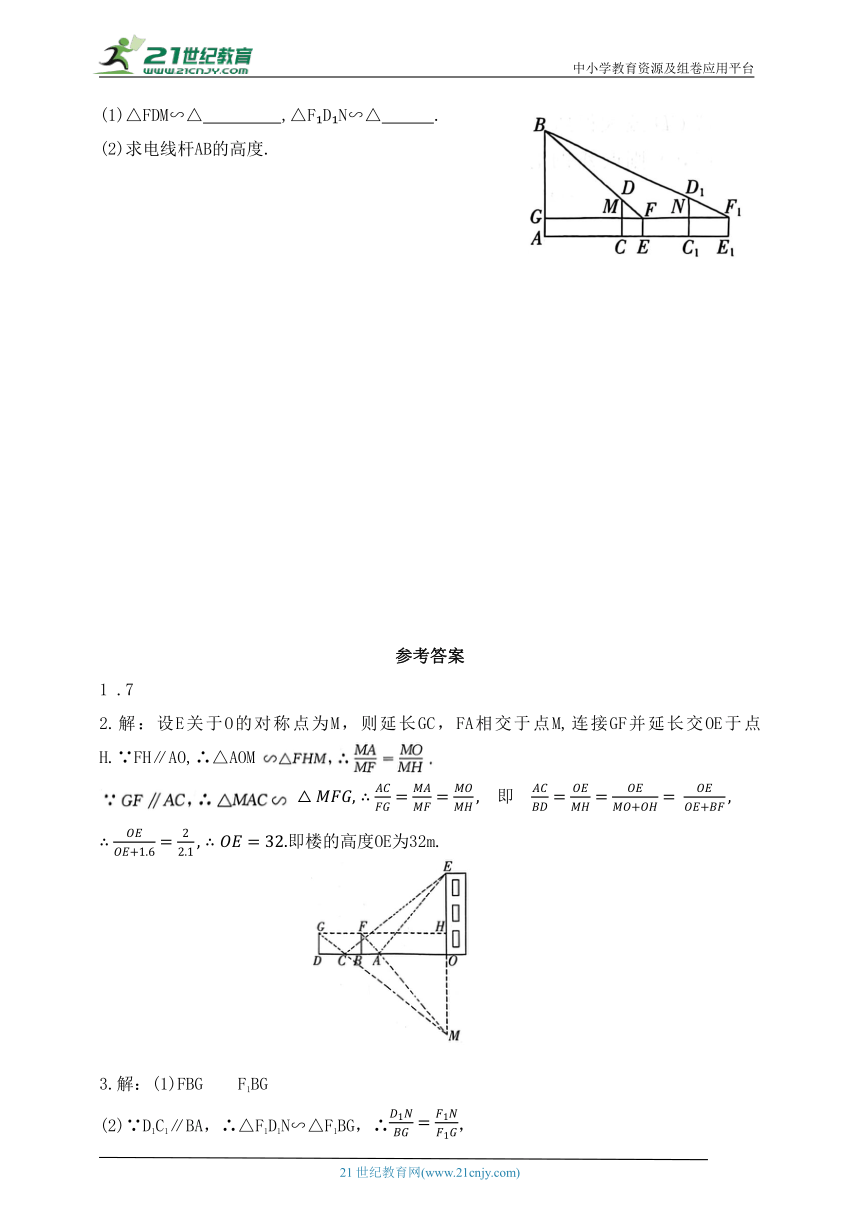
(1)△FDM∽△ ,△F D N∽△ .
(2)求电线杆AB的高度.
参考答案
1 .7
2.解:设E关于O的对称点为M,则延长GC,FA相交于点M,连接GF并延长交OE于点H.∵FH∥AO,∴△AOM
即
即楼的高度OE为32m.
3.解:(1)FBG F1BG
(2)∵D1C1∥BA,∴△F1D1N∽△F1BG,∴,
∵DC∥BA,∴△FDM∽△FBG,
即电线杆AB的高度为15m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
相似三角形的实际应用
1.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水面C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为 米.
2.如图,为了测量一栋楼的高度OE,小明同学先在操场上A处放一面镜子,向后退到B处,恰好在镜子中看到楼的顶部E;再将镜子放到C处,然后后退到D处,恰好再次在镜子中看到楼的顶部E(O,A,B,C,D在同一条直线上),测得AC=2m,BD=2.1m,如果小明的眼睛距地面的高度BF,DG为1.6m,试确定楼的高度OE.
3.如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C 处直立高3m的竹竿C D ,然后退到点E 处,此时恰好看到竹竿顶端D 与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m, EC =6m,C E =3m.
(1)△FDM∽△ ,△F D N∽△ .
(2)求电线杆AB的高度.
参考答案
1 .7
2.解:设E关于O的对称点为M,则延长GC,FA相交于点M,连接GF并延长交OE于点H.∵FH∥AO,∴△AOM
即
即楼的高度OE为32m.
3.解:(1)FBG F1BG
(2)∵D1C1∥BA,∴△F1D1N∽△F1BG,∴,
∵DC∥BA,∴△FDM∽△FBG,
即电线杆AB的高度为15m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
