专项训练 相似三角形与特殊四边形、一元二次方程(含答案)
文档属性
| 名称 | 专项训练 相似三角形与特殊四边形、一元二次方程(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
相似三角形与特殊四边形、一元二次方程
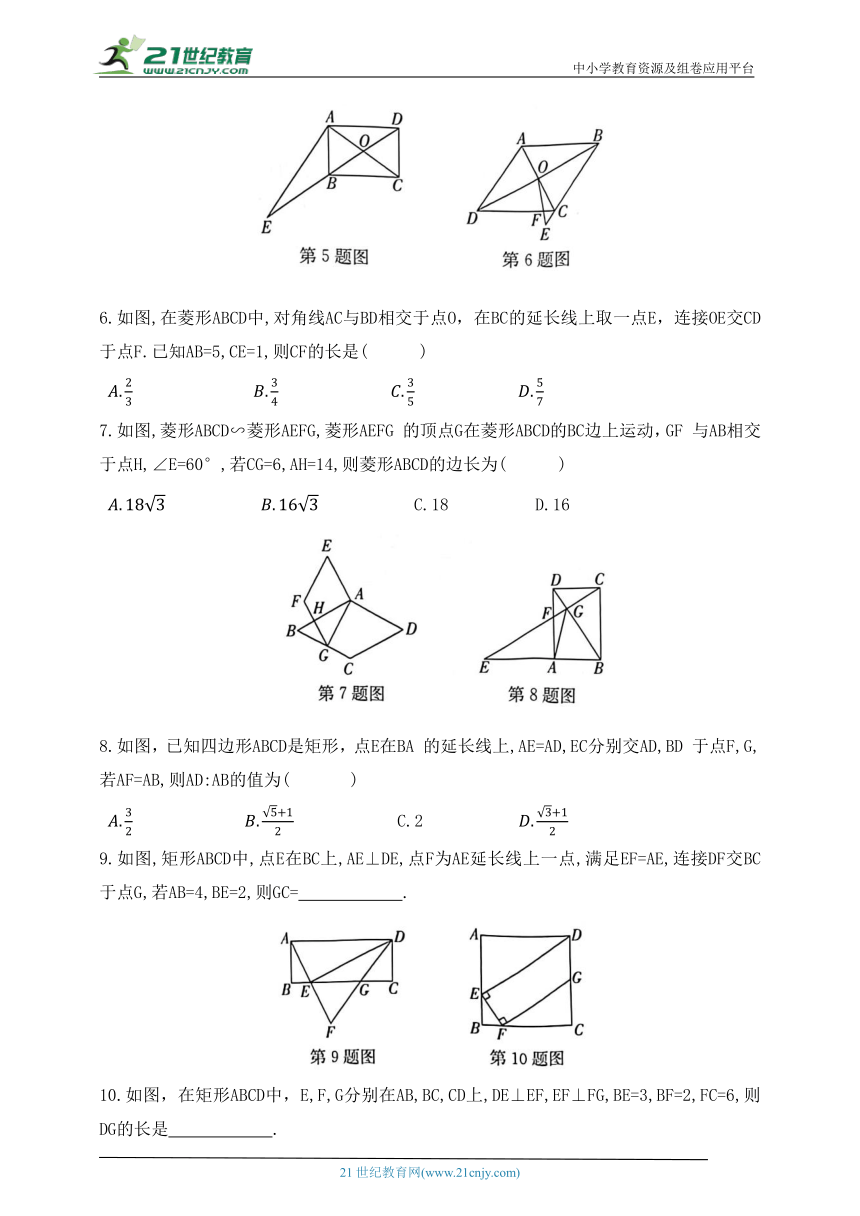
1.如图,菱形ABCD中,点B的坐标为(2,1),点C的坐标为(1,0),点D在y轴正半轴上,以点C为位似中心,在x轴的下方作菱形ABCD的位似图形菱形并把菱形ABCD的边长放大到原来的2倍,则点B的对应点的横坐标是( )
A.- 1 .5 B.-0.5 C.-2 D.-1
2.如图,在矩形ABCD中, E是BC的中点,AE⊥BD于点F,则CF的长是( )
A.1 B.1 .2 D.2
3.如图,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD=3BF,BE=4,则AD的长为( )
A.9 B.12 C.15 D.18
4.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积为( )
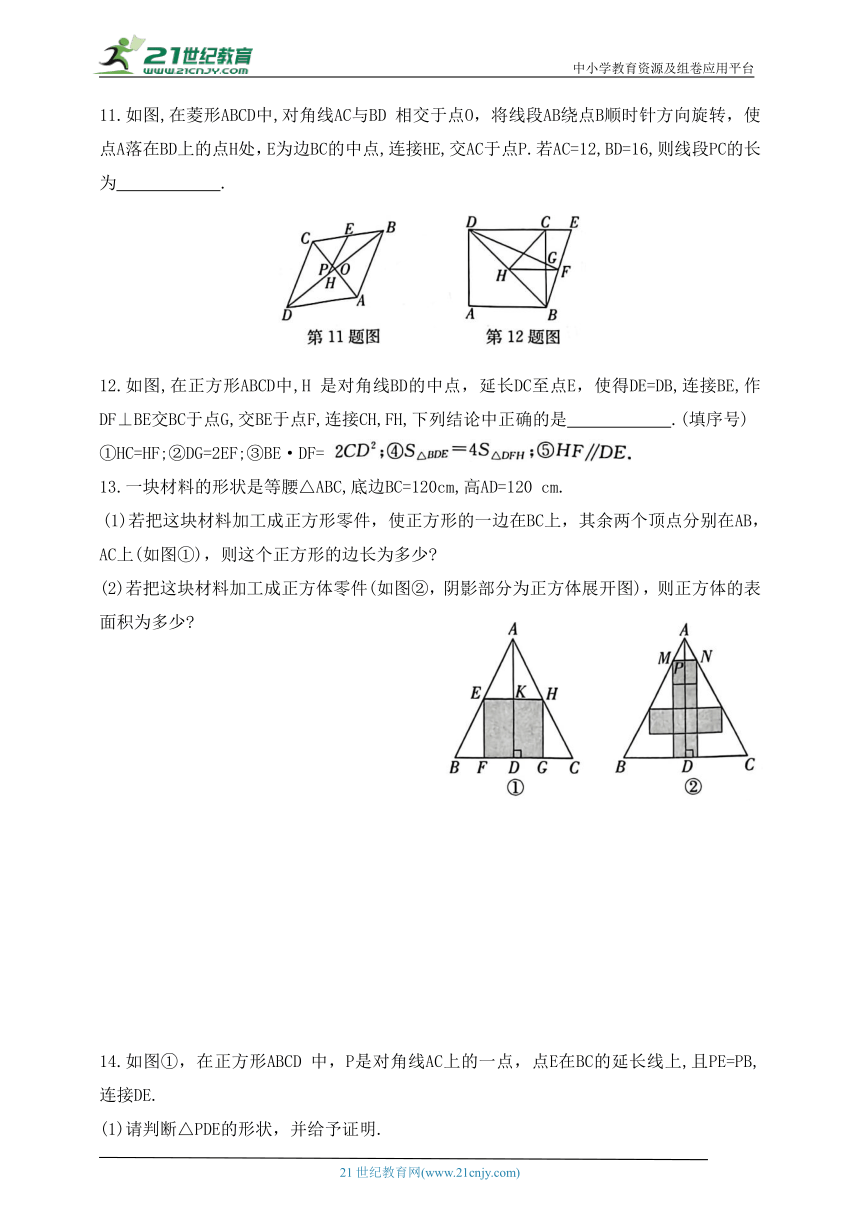
5.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值是( )
6.如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知AB=5,CE=1,则CF的长是( )
7.如图,菱形ABCD∽菱形AEFG,菱形AEFG 的顶点G在菱形ABCD的BC边上运动,GF 与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
C.18 D.16
8.如图,已知四边形ABCD是矩形,点E在BA 的延长线上,AE=AD,EC分别交AD,BD 于点F,G,若AF=AB,则AD:AB的值为( )
C.2
9.如图,矩形ABCD中,点E在BC上,AE⊥DE,点F为AE延长线上一点,满足EF=AE,连接DF交BC于点G,若AB=4,BE=2,则GC= .
10.如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是 .
11.如图,在菱形ABCD中,对角线AC与BD 相交于点O,将线段AB绕点B顺时针方向旋转,使点A落在BD上的点H处,E为边BC的中点,连接HE,交AC于点P.若AC=12,BD=16,则线段PC的长为 .
12.如图,在正方形ABCD中,H 是对角线BD的中点,延长DC至点E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH,FH,下列结论中正确的是 .(填序号)
①HC=HF;②DG=2EF;③BE·DF=
13.一块材料的形状是等腰△ABC,底边BC=120cm,高AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上(如图①),则这个正方形的边长为多少
(2)若把这块材料加工成正方体零件(如图②,阴影部分为正方体展开图),则正方体的表面积为多少
14.如图①,在正方形ABCD 中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB,连接DE.
(1)请判断△PDE的形状,并给予证明.
(2)把正方形ABCD改为菱形,且其他条件不变(如图②),求 的值.
参考答案
1.D 2.C 3.C
4.B [解析]如图,设BF与CE相交于点
在菱形ECGF中,
即 解得
∵∠A=120°,易得菱形ABCD的CD边上的高为
菱形ECGF的CE边长的高为
图中阴影部分的面积
5.A [解析]如图,过点B作BF⊥AC于点F.
∵四边形ABCD为矩形,∴OA=OB=OC=OD,∠ABC=90°.
在Rt△ABC中.
在Rt△OBF中,
∴∠OAE=90°,∴∠OFB=∠OAE.
∵∠AOE=∠FOB, 解得AE=
6.D [解析]如图,过点O作OG∥CD交BC于点G.
∵四边形ABCD是菱形,且AB=5,∴BC=CD=AB=5,OB=OD.
∴GO=
∴CF=
7.C [解析]如图,连接AC.
∵菱形ABCD∽菱形AEFG,∴∠B=∠E=∠AGF=60°,AB=BC,
∴△ABC是等边三角形,∴∠ACB=60°.
设AB=BC=AC=a,则BH=a-14,BG=a-6.
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,∠AGH=∠ACG=60°,∴∠BGH=∠CAG.
即 或2(舍去),
∴AB=18.
8.B [解析]∵四边形ABCD是矩形,∴AE∥CD,∴∠AEF
.
设AE=AD=a(a>0),AF=AB=b(b>0),∴a·(a-b)=b .化简得 a -ab-b =0.
解得 或 (舍去),∴AD:AB=a:b
9.3
11.5 [解析]如图,过点E作EF⊥BD于点F.
∵四边形ABCD是菱形,∴AC⊥BD,∴EF∥AC.
∵AC=12,BD
=10,∴OH=BH-OB=2.
∵E是BC的中点,EF∥
即
12.①②④⑤ [解析]∵DE=DB,DF⊥BE,∴BF=EF.
又 ∥
∵正方形ABCD中, 故①⑤正确.
∵∠DGC=∠BGF,∠DCG=∠GFB=90°,∴∠CBE=∠CDG.
∵∠DCG=∠BCE=90°,DC=BC,∴△DCG≌△BCE(ASA),∴DG=BE,∴DG=2EF,故②正确.
∵∠DEF=∠CEB,∠DFE=∠BCE=90°,∴△DFE∽△
DE,而DE≠2CD,故③不正确.
∵H是对角线BD的中点,
故④正确.
13.解:(1)设正方形的边长EH为x cm.
∵AD是△ABC的高,∴∠ADB=90°.
∵四边形EFGH是正方形,∴EH∥
即 解得x=60.
答:这个正方形的边长为60cm.
(2)设正方形的边长MN为a cm.
∵MN∥BC,∴△AMN∽△ABC, 即 解得a=24,∴6a =6×24 =3456. 答:正方体的表面积为3456cm .
14.解:(1)△PDE为等腰直角三角形.
证明:∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°.
在△BCP和△DCP中 (SAS),∴∠CBP=∠CDP,PD=PB.
∵PE=PB,∴∠CBP=∠CEP,PD=PE.
∵∠CFE=∠PFD,∴180°-∠PFD-∠CDP=180°-∠CFE-∠CEP,即∠DPE=∠DCE=90°,
∴△PDE为等腰直角三角形.
(2)∵四边形ABCD为菱形,∴AB∥CD,BC=DC,∠BCP=∠DCP.
在△BCP和△DCP 中,
∴∠CBP=∠CDP,PD=PB.
∵PE=PB,∴∠CBP=∠CEP,PD=PE.
∵∠CFE=∠PFD,∴180°-∠PFD-∠CDP=180°-∠CFE-∠CEP,即∠DPE=∠DCE.
∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
∵△ABC,△DPE是等腰三角形,∴△ABC∽△DPE,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
相似三角形与特殊四边形、一元二次方程
1.如图,菱形ABCD中,点B的坐标为(2,1),点C的坐标为(1,0),点D在y轴正半轴上,以点C为位似中心,在x轴的下方作菱形ABCD的位似图形菱形并把菱形ABCD的边长放大到原来的2倍,则点B的对应点的横坐标是( )
A.- 1 .5 B.-0.5 C.-2 D.-1
2.如图,在矩形ABCD中, E是BC的中点,AE⊥BD于点F,则CF的长是( )
A.1 B.1 .2 D.2
3.如图,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD=3BF,BE=4,则AD的长为( )
A.9 B.12 C.15 D.18
4.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积为( )
5.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则 的值是( )
6.如图,在菱形ABCD中,对角线AC与BD相交于点O,在BC的延长线上取一点E,连接OE交CD于点F.已知AB=5,CE=1,则CF的长是( )
7.如图,菱形ABCD∽菱形AEFG,菱形AEFG 的顶点G在菱形ABCD的BC边上运动,GF 与AB相交于点H,∠E=60°,若CG=6,AH=14,则菱形ABCD的边长为( )
C.18 D.16
8.如图,已知四边形ABCD是矩形,点E在BA 的延长线上,AE=AD,EC分别交AD,BD 于点F,G,若AF=AB,则AD:AB的值为( )
C.2
9.如图,矩形ABCD中,点E在BC上,AE⊥DE,点F为AE延长线上一点,满足EF=AE,连接DF交BC于点G,若AB=4,BE=2,则GC= .
10.如图,在矩形ABCD中,E,F,G分别在AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是 .
11.如图,在菱形ABCD中,对角线AC与BD 相交于点O,将线段AB绕点B顺时针方向旋转,使点A落在BD上的点H处,E为边BC的中点,连接HE,交AC于点P.若AC=12,BD=16,则线段PC的长为 .
12.如图,在正方形ABCD中,H 是对角线BD的中点,延长DC至点E,使得DE=DB,连接BE,作DF⊥BE交BC于点G,交BE于点F,连接CH,FH,下列结论中正确的是 .(填序号)
①HC=HF;②DG=2EF;③BE·DF=
13.一块材料的形状是等腰△ABC,底边BC=120cm,高AD=120 cm.
(1)若把这块材料加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上(如图①),则这个正方形的边长为多少
(2)若把这块材料加工成正方体零件(如图②,阴影部分为正方体展开图),则正方体的表面积为多少
14.如图①,在正方形ABCD 中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB,连接DE.
(1)请判断△PDE的形状,并给予证明.
(2)把正方形ABCD改为菱形,且其他条件不变(如图②),求 的值.
参考答案
1.D 2.C 3.C
4.B [解析]如图,设BF与CE相交于点
在菱形ECGF中,
即 解得
∵∠A=120°,易得菱形ABCD的CD边上的高为
菱形ECGF的CE边长的高为
图中阴影部分的面积
5.A [解析]如图,过点B作BF⊥AC于点F.
∵四边形ABCD为矩形,∴OA=OB=OC=OD,∠ABC=90°.
在Rt△ABC中.
在Rt△OBF中,
∴∠OAE=90°,∴∠OFB=∠OAE.
∵∠AOE=∠FOB, 解得AE=
6.D [解析]如图,过点O作OG∥CD交BC于点G.
∵四边形ABCD是菱形,且AB=5,∴BC=CD=AB=5,OB=OD.
∴GO=
∴CF=
7.C [解析]如图,连接AC.
∵菱形ABCD∽菱形AEFG,∴∠B=∠E=∠AGF=60°,AB=BC,
∴△ABC是等边三角形,∴∠ACB=60°.
设AB=BC=AC=a,则BH=a-14,BG=a-6.
∵∠AGB=∠AGH+∠BGH=∠ACG+∠CAG,∠AGH=∠ACG=60°,∴∠BGH=∠CAG.
即 或2(舍去),
∴AB=18.
8.B [解析]∵四边形ABCD是矩形,∴AE∥CD,∴∠AEF
.
设AE=AD=a(a>0),AF=AB=b(b>0),∴a·(a-b)=b .化简得 a -ab-b =0.
解得 或 (舍去),∴AD:AB=a:b
9.3
11.5 [解析]如图,过点E作EF⊥BD于点F.
∵四边形ABCD是菱形,∴AC⊥BD,∴EF∥AC.
∵AC=12,BD
=10,∴OH=BH-OB=2.
∵E是BC的中点,EF∥
即
12.①②④⑤ [解析]∵DE=DB,DF⊥BE,∴BF=EF.
又 ∥
∵正方形ABCD中, 故①⑤正确.
∵∠DGC=∠BGF,∠DCG=∠GFB=90°,∴∠CBE=∠CDG.
∵∠DCG=∠BCE=90°,DC=BC,∴△DCG≌△BCE(ASA),∴DG=BE,∴DG=2EF,故②正确.
∵∠DEF=∠CEB,∠DFE=∠BCE=90°,∴△DFE∽△
DE,而DE≠2CD,故③不正确.
∵H是对角线BD的中点,
故④正确.
13.解:(1)设正方形的边长EH为x cm.
∵AD是△ABC的高,∴∠ADB=90°.
∵四边形EFGH是正方形,∴EH∥
即 解得x=60.
答:这个正方形的边长为60cm.
(2)设正方形的边长MN为a cm.
∵MN∥BC,∴△AMN∽△ABC, 即 解得a=24,∴6a =6×24 =3456. 答:正方体的表面积为3456cm .
14.解:(1)△PDE为等腰直角三角形.
证明:∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°.
在△BCP和△DCP中 (SAS),∴∠CBP=∠CDP,PD=PB.
∵PE=PB,∴∠CBP=∠CEP,PD=PE.
∵∠CFE=∠PFD,∴180°-∠PFD-∠CDP=180°-∠CFE-∠CEP,即∠DPE=∠DCE=90°,
∴△PDE为等腰直角三角形.
(2)∵四边形ABCD为菱形,∴AB∥CD,BC=DC,∠BCP=∠DCP.
在△BCP和△DCP 中,
∴∠CBP=∠CDP,PD=PB.
∵PE=PB,∴∠CBP=∠CEP,PD=PE.
∵∠CFE=∠PFD,∴180°-∠PFD-∠CDP=180°-∠CFE-∠CEP,即∠DPE=∠DCE.
∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
∵△ABC,△DPE是等腰三角形,∴△ABC∽△DPE,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
