专项训练 相似型几何综合题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
相似型几何综合题
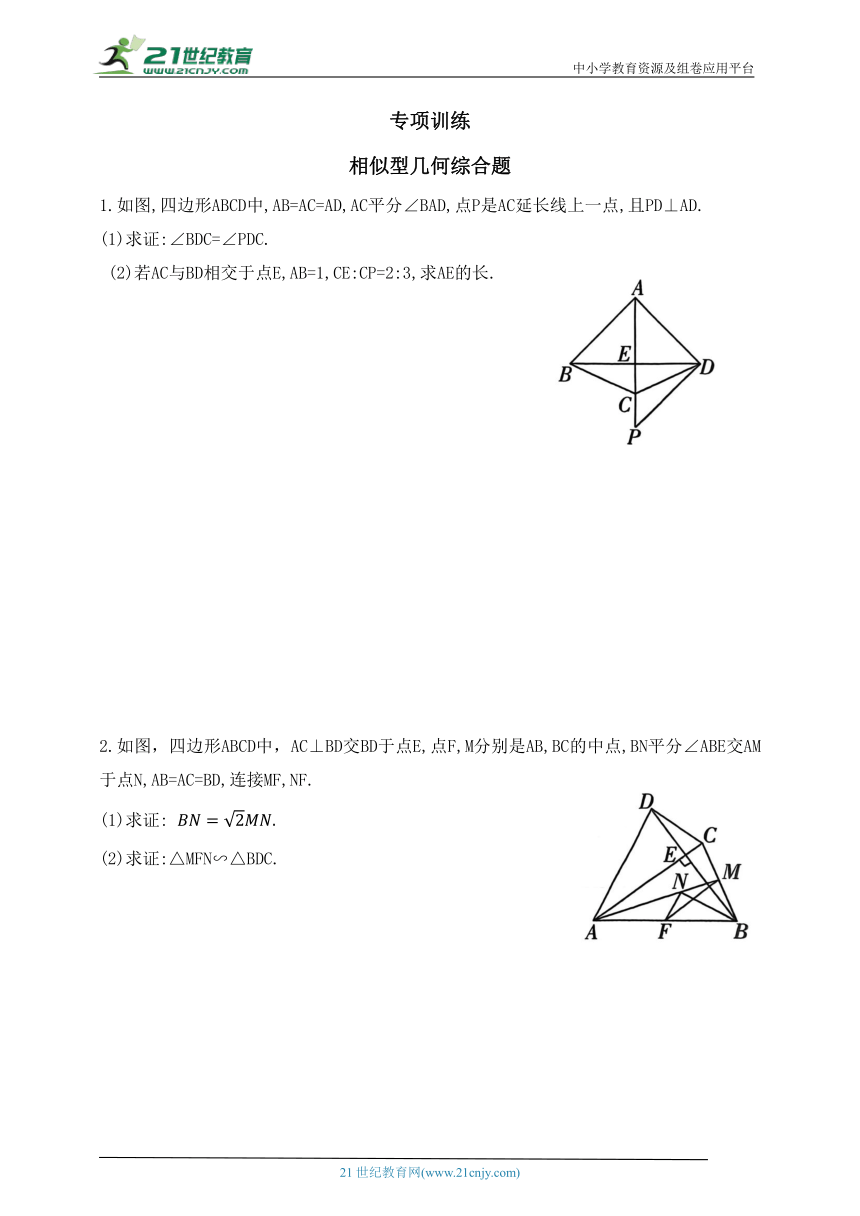
1.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)求证:∠BDC=∠PDC.
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
2.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)求证:
(2)求证:△MFN∽△BDC.
3.已知矩形ABCD,点E是AD上一点,将矩形沿BE折叠,点A恰好落在BD上的点F处.
(1)如图①,若AB=3,AD=4,求AE的长.
(2)如图②,若点F恰好是BD的中点,点M 是BD上一点,过点M作MN∥BE交AD于点N,连接EM,若MN平分∠EMD,求证:DN ·DE=DM· BM.
4.如图,正方形ABCD中,点P 为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.
(1)请找出图中一对相似三角形,并证明.
(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.
参考答案
1.(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90° .
∵AC=AD,∴∠ACD =∠ADC,∴∠ADC+∠BDC=90°.
∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC.
(2)解:如图,过点C作CM⊥PD于点M.
∵∠BDC=∠PDC,∴CE=CM.
∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△
设CM=CE=x.∵CE:CP=2:3,
解得 故
2.证明:(1)∵AB=AC,点M是BC的中点,∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,∴∠EBN=∠ABN.
∵AC⊥BD,∴∠AEB=90°,∴∠EAB+∠EBA
∠ABE)=45°,
∴△BMN是等腰直角三角形,∴BN=
(2)∵点F,M分别是AB,BC的中点,∴FM∥AC,FM=
∵AC=BD,∴FM=,即
是等腰直角三角形
即∠FMB=90°.
∵FM∥AC,∴∠ACB=∠FMB.
∵∠CEB=90°,∴∠ACB+∠CBD=90°,∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD,∴△MFN∽△BDC.
3.(1)解:由题意知∠BAD=90°,AB=3,AD=4,∴BD=
=90°,∴∠EFD=90°,∴∠EFD=∠A.
∵∠EDF=∠ADB,∴△DEF∽△DBA,∴
设AE=EF=x,则 解得
(2)证明:∵F为BD的中点,∠A=∠BFE=90°,∴BE=DE,∴∠EBD=∠EDB.
∵MN∥BE,∴∠NME=∠BEM.又∵MN平分∠EMD,∴∠NMD=∠NME,
4.解:
(1)△ADQ∽△EPD.证明:∵PE⊥DQ,∴∠DEP=∠A=90°.
∵∠ADC=90°,∴∠ADQ+∠EDP=90°.
又∵∠EDP+∠DPE=90°,∴∠ADQ=∠DPE,∴△ADQ∽△EPD.
(2)∵AB=4,点Q为AB的中点,
∵∠PEQ=∠A=90°,∴若以点P,E,Q为顶点的三角形与△ADQ相似,有两种情况:
①当△ADQ∽△EPQ时, 设EQ=x,则EP=2x,则
由(1)知△ 即 ②当△ADQ∽△EQP时,设EQ=2a,则EP=a.同理可得
综上,DP的长为2或5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
相似型几何综合题
1.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)求证:∠BDC=∠PDC.
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
2.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)求证:
(2)求证:△MFN∽△BDC.
3.已知矩形ABCD,点E是AD上一点,将矩形沿BE折叠,点A恰好落在BD上的点F处.
(1)如图①,若AB=3,AD=4,求AE的长.
(2)如图②,若点F恰好是BD的中点,点M 是BD上一点,过点M作MN∥BE交AD于点N,连接EM,若MN平分∠EMD,求证:DN ·DE=DM· BM.
4.如图,正方形ABCD中,点P 为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.
(1)请找出图中一对相似三角形,并证明.
(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.
参考答案
1.(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90° .
∵AC=AD,∴∠ACD =∠ADC,∴∠ADC+∠BDC=90°.
∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC.
(2)解:如图,过点C作CM⊥PD于点M.
∵∠BDC=∠PDC,∴CE=CM.
∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△
设CM=CE=x.∵CE:CP=2:3,
解得 故
2.证明:(1)∵AB=AC,点M是BC的中点,∴AM⊥BC,AM平分∠BAC.
∵BN平分∠ABE,∴∠EBN=∠ABN.
∵AC⊥BD,∴∠AEB=90°,∴∠EAB+∠EBA
∠ABE)=45°,
∴△BMN是等腰直角三角形,∴BN=
(2)∵点F,M分别是AB,BC的中点,∴FM∥AC,FM=
∵AC=BD,∴FM=,即
是等腰直角三角形
即∠FMB=90°.
∵FM∥AC,∴∠ACB=∠FMB.
∵∠CEB=90°,∴∠ACB+∠CBD=90°,∴∠CBD+∠FMB=90°,
∴∠NMF=∠CBD,∴△MFN∽△BDC.
3.(1)解:由题意知∠BAD=90°,AB=3,AD=4,∴BD=
=90°,∴∠EFD=90°,∴∠EFD=∠A.
∵∠EDF=∠ADB,∴△DEF∽△DBA,∴
设AE=EF=x,则 解得
(2)证明:∵F为BD的中点,∠A=∠BFE=90°,∴BE=DE,∴∠EBD=∠EDB.
∵MN∥BE,∴∠NME=∠BEM.又∵MN平分∠EMD,∴∠NMD=∠NME,
4.解:
(1)△ADQ∽△EPD.证明:∵PE⊥DQ,∴∠DEP=∠A=90°.
∵∠ADC=90°,∴∠ADQ+∠EDP=90°.
又∵∠EDP+∠DPE=90°,∴∠ADQ=∠DPE,∴△ADQ∽△EPD.
(2)∵AB=4,点Q为AB的中点,
∵∠PEQ=∠A=90°,∴若以点P,E,Q为顶点的三角形与△ADQ相似,有两种情况:
①当△ADQ∽△EPQ时, 设EQ=x,则EP=2x,则
由(1)知△ 即 ②当△ADQ∽△EQP时,设EQ=2a,则EP=a.同理可得
综上,DP的长为2或5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
