专项训练 分类讨论在相似三角形中的应用(含答案)
文档属性
| 名称 | 专项训练 分类讨论在相似三角形中的应用(含答案) | 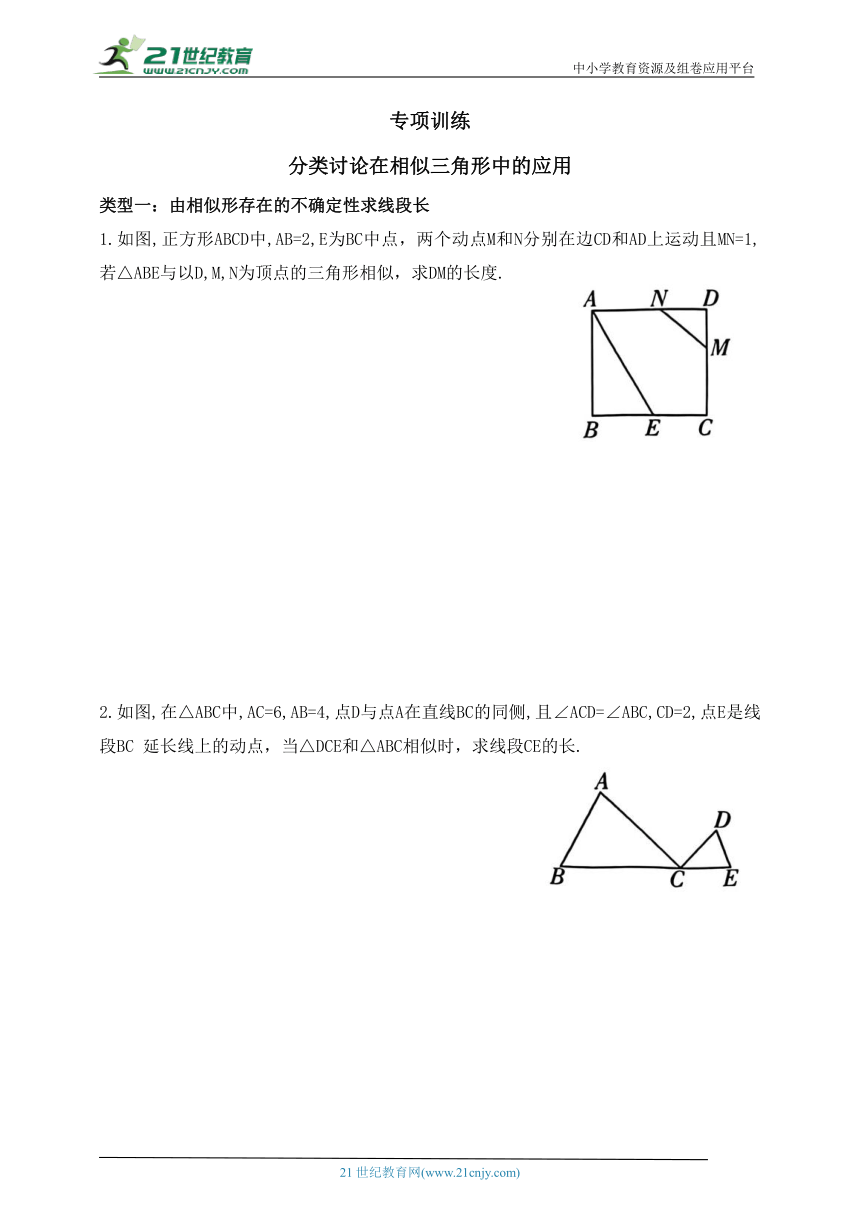 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-17 19:40:31 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
分类讨论在相似三角形中的应用
类型一:由相似形存在的不确定性求线段长
1.如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D,M,N为顶点的三角形相似,求DM的长度.
2.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC 延长线上的动点,当△DCE和△ABC相似时,求线段CE的长.
类型二:由等腰三角形存在的不确定性求线段长或角度
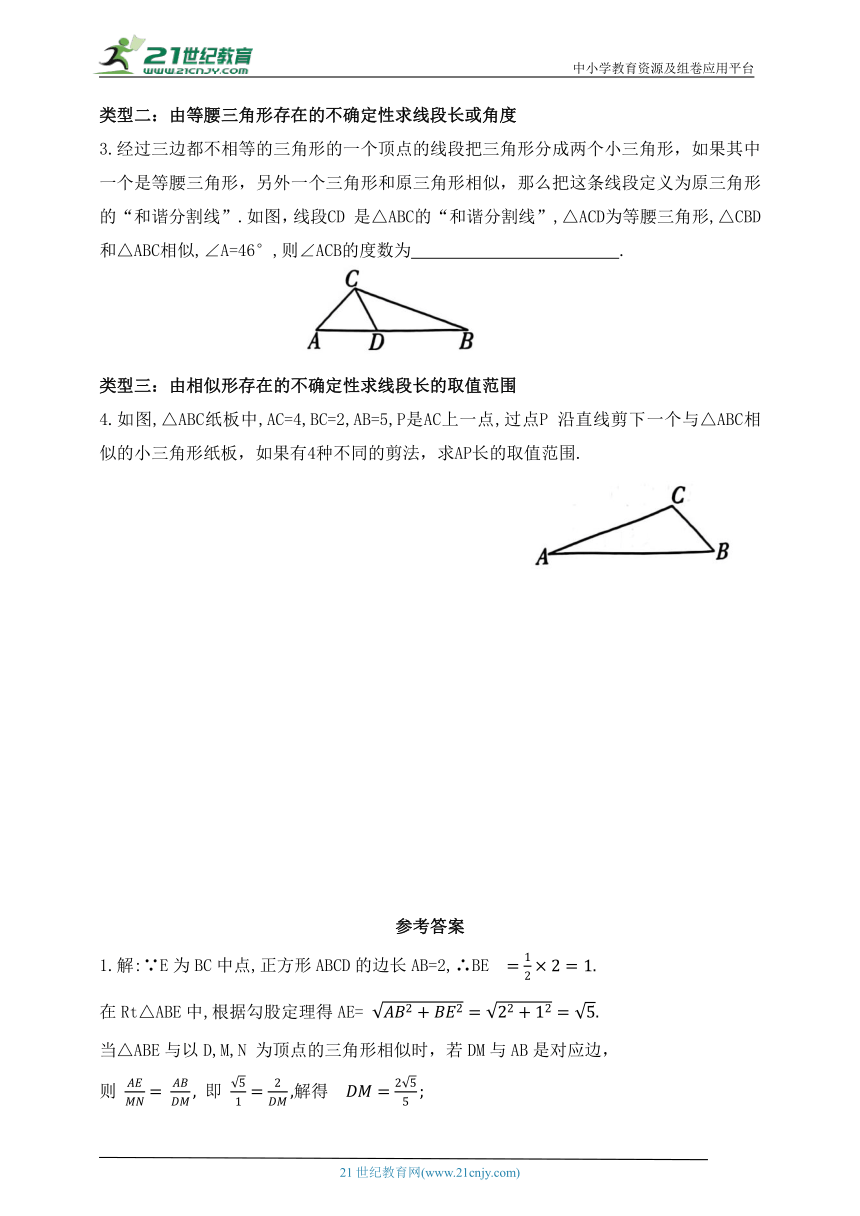
3.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD 是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .
类型三:由相似形存在的不确定性求线段长的取值范围
4.如图,△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P 沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,求AP长的取值范围.
参考答案
1.解:∵E为BC中点,正方形ABCD的边长AB=2,∴BE
在Rt△ABE中,根据勾股定理得AE=
当△ABE与以D,M,N 为顶点的三角形相似时,若DM与AB是对应边,
则 即 解得
若DM与BE是对应边,则 即 解得
综上所述, 或
2.解:∵∠A+∠ABC+∠ACB=∠ACB+∠ACD+∠DCE=180°,∠ACD=∠ABC,
∴∠A=∠DCE,∴当△DCE和△ABC相似时,有 或
或 解得CE=3或
3.113°或92° [解析]∵△BCD∽△BAC,∴∠BCD=∠A =46°.
∵△ACD是等腰三角形,∠ADC>∠BCD,∴∠ADC>∠A,即AC≠CD.
①当AC=AD时,∠ACD113°.
②当DA=DC时,∠ACD=∠A=46°,∴∠ACB=46°+46°=92°.
故答案为113°或92°.
4.解:如图①所示,过点P作PD∥AB,交BC于点D,或作PE∥BC,交AB于点E,则△PCD∽△ACB或△APE∽△ACB,此时0<AP<4.
如图②所示,过点P作∠APF=∠B,交AB于点F,则△APF∽△ABC,此时0<AP<4.
如图③所示,过点P作∠CPG=∠CBA,交BC于点G,则△CPG∽△CBA,当点G与点B重合时, CB =CP· CA,即2 =4CP,∴CP=1,AP=3,∴此时3≤AP<4.
综上所述,AP长的取值范围是3≤AP<4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
分类讨论在相似三角形中的应用
类型一:由相似形存在的不确定性求线段长
1.如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D,M,N为顶点的三角形相似,求DM的长度.
2.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC 延长线上的动点,当△DCE和△ABC相似时,求线段CE的长.
类型二:由等腰三角形存在的不确定性求线段长或角度
3.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD 是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为 .
类型三:由相似形存在的不确定性求线段长的取值范围
4.如图,△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P 沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,求AP长的取值范围.
参考答案
1.解:∵E为BC中点,正方形ABCD的边长AB=2,∴BE
在Rt△ABE中,根据勾股定理得AE=
当△ABE与以D,M,N 为顶点的三角形相似时,若DM与AB是对应边,
则 即 解得
若DM与BE是对应边,则 即 解得
综上所述, 或
2.解:∵∠A+∠ABC+∠ACB=∠ACB+∠ACD+∠DCE=180°,∠ACD=∠ABC,
∴∠A=∠DCE,∴当△DCE和△ABC相似时,有 或
或 解得CE=3或
3.113°或92° [解析]∵△BCD∽△BAC,∴∠BCD=∠A =46°.
∵△ACD是等腰三角形,∠ADC>∠BCD,∴∠ADC>∠A,即AC≠CD.
①当AC=AD时,∠ACD113°.
②当DA=DC时,∠ACD=∠A=46°,∴∠ACB=46°+46°=92°.
故答案为113°或92°.
4.解:如图①所示,过点P作PD∥AB,交BC于点D,或作PE∥BC,交AB于点E,则△PCD∽△ACB或△APE∽△ACB,此时0<AP<4.
如图②所示,过点P作∠APF=∠B,交AB于点F,则△APF∽△ABC,此时0<AP<4.
如图③所示,过点P作∠CPG=∠CBA,交BC于点G,则△CPG∽△CBA,当点G与点B重合时, CB =CP· CA,即2 =4CP,∴CP=1,AP=3,∴此时3≤AP<4.
综上所述,AP长的取值范围是3≤AP<4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
